
Chap 2 导数和微分
Chap 2 导数和微分

Chap 2.1 导数的概念
Chap 2.1 导数的概念

2.1.1 例子 速度 运动物体的路程函数S() 时间从t0→t+△t,路程△S=S(t+△t)-S(to) △S 平均速度: △t 时刻的瞬时速度: △S lim=lim S(t+△t)-S(t) △1-→0△t △1-→0 △t 斜率 求函数曲线y=f(x)上点M(xyo)处的切线
2.1.1 例子 速度 运动物体的路程函数 S(t) 时间从t0→t0+Δt,路程ΔS= S(t0+Δt)-S(t0) 平均速度: tSΔΔ t0时刻的瞬时速度: t tSttS t S t t Δ Δ+ − = Δ Δ →Δ →Δ )()( lim lim 0 0 0 0 ■ 斜率 求函数曲线y = f (x)上点M0(x0,y0)处的切线
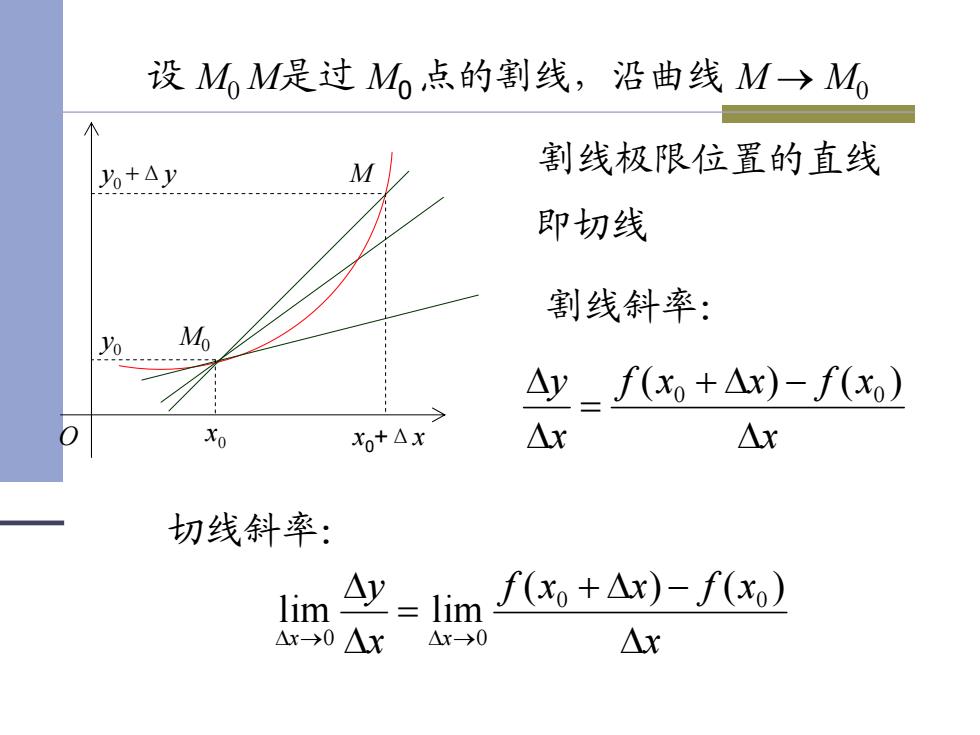
设MM是过M点的割线,沿曲线M→M, N o+Ay M 割线极限位置的直线 即切线 割线斜率: Yo M △y_f(x+△x)-f(x) xo+Ax △x △x 切线斜率: lim Ay lim f(x+△x)-f(x) △r→0△x x→0 △x
x0 y0 x0+Δx y0 +Δy M0 M O 设 M0 M是过 M0 点的割线,沿曲线 M → M0 割线极限位置的直线 即切线 割线斜率: x xfxxf x y Δ + Δ − = Δ Δ )()( 0 0 切线斜率: x xfxxf x y x x Δ + Δ − = Δ Δ →Δ →Δ )()( lim lim 0 0 0 0

细菌增殖速度 设一菌群在某一时刻t的细菌数为N() 求该菌群在时刻t。的增殖速度v(o) t,>t+△t一段的平均增殖速度 △N_N(t。+△t)-m(to) △t △t t,,点的增殖速度 AN v(to)=lim=lim N(t。+△t)-N() △-→0△t △x→0 △t
细菌增殖速度 设一菌群在某一时刻 设一菌群在某一时刻t 的细菌数为 N (t) 求该菌群在时刻 求该菌群在时刻t0 的增殖速度 v(t0) t0 → t0+Δt 一段的平均增殖速度 0 0 N Nt t mt ( ) () t t Δ + Δ − = Δ Δ t0 点的增殖速度 0 0 0 0 0 ( ) () ( ) lim lim t x N Nt t Nt v t t t Δ→ Δ→ Δ +Δ − = = Δ Δ

2.1.2导数定义 若y=f(x)在x=x的邻域有定义,则 im f x→x0 x-Xo 称为y=f(x)在xo点的导数(或微商) 也可以用增量的写法 f,)=m女 Ax-→0△x 导数的其他记号 df(x.) d斯 (f也可写为y) dx dx
2.1.2 导数定义 0 0 0 )()( lim)( 0 xx xfxf xf xx def − − ′ = → x f xf x Δ Δ ′ = →Δ 0 0 lim)( 称为y = f (x ) 在 x 0点的导数 ( 或微商 ) 也可以用增量的写法 ■ 若y = f (x ) 在x = x 0的邻域有定义,则 导数的其他记号 0 0 , )( , 0 xx xx dx df dx xdf f = = ′ ( f 也可写为 y )

>几何意义:函数曲线在该点切线的斜率 > lim Ax0△X 时导数不存在,但可以说导数 为0,此时曲线在该点切线与x轴垂直 单侧导数 右导数」 f(xo)=lim M △x→0 △x 左导数 f(x)=lim △f Ax-0△X f"(x)存在台f(x),f'(x)存在且相等
¾ 几何意义:函数曲线在该点切线的斜率 ¾ ∞= Δ Δ →Δ x f x 0 lim 时导数不存在,但可以说导数 为∞,此时曲线在该点切线与x轴垂直 ■ 单侧导数 x f xf x Δ Δ ′ = + →Δ + 0 0 右导数 lim)( 左导数 x f xf x Δ Δ ′ = − →Δ − 0 0 lim)( ¾ ′ xf 0 )( 存在 ⇔ + 0 , −′′ xfxf 0 )()( 存在且相等

例若f'(x)=A,f(x)=B,求 (1)lim f(xo+3h)-f(xo) h-→0 h (2)lim f(x+2h)-f(x。-h) -→0 h (3)1im f2(x。+2h)-f2(x0-h) h-→0 h 例若mf+创f-m=0, 能否推出 h30 h f'(x)=0?
例 若 ′ 0 = 0 = BxfAxf ,)(,)( 求 h xfhxf h )()3( lim)1( 0 0 0 + − → h hxfhxf h )()2( lim)2( 0 0 0 + − − → h hxfhxf h )()2( lim)3( 0 2 0 2 0 −−+ → 例 若 0 0 0 ( )( ) lim 0, h fx h fx h → h + − − = 0 f x ′( ) 0? 能否推出 =

导函数 y=f(x)在区间I内每点有导数,在I的闭端点 有单侧导数,则称函数f(x)在区间I可导,记为 f(x)∈D(),f'(x)称为f(x)的导函数 例求下列函数的导函数 (1)f(x)=c (2)f(x)=xm; (3)f(x)=sinx (4)y=a* (5)f(x)=logx
■ 导函数 y = f (x)在区间I 内每点有导数,在I 的闭端点 有单侧导数,则称函数 f (x)在区间I 可导,记为 f (x)∈D(I),f ’(x)称为f (x)的导函数 例 求下列函数的导函数 (1) ( ) fx c = (3) ( ) sin f x x = ;)()2( m = xxf x )4( = ay xxf a = log)()5(

导出 (c)'=0 (xm)'=mxm-1 (sinx)'=cosx (cosx)'=-sinx (a")'-a*Ina (e)'=e (I08。x= xIna (Inxy'=I x 例求曲线y=sinx在x=π/3处的切线及法线 方程
c ′ = 0)( 1 )( − ′ = m m mxx ′ = cos)(sin xx aaa xx ′ = ln)( ′ = −sin)(cos xx xx )( ′ = ee 1 (log ) ln a x x a ′ = 导出 1 (ln ) x x ′ = 例 求曲线y=sinx 在x =π/ 3 处的切线及法线 方程