
第四章理论分布与抽样分布 &4.1事件与概率 &4.2随机变量的概率分布类型 &4.3理论分布 &4.4抽样分布 I
第四章 理论分布与抽样分布 &4.1 事件与概率 &4.2 随机变量的概率分布类型 &4.3 理论分布 &4.4 抽样分布

&4.1事件与概率 、 事件及其相互关系 (一)事件的意义 1.必然事件 2.不可能事件 3.随机事件 在一定条件下,可能发生,也可能不 发生的现象称为随机事件
在一定条件下,可能发生,也可能不 发生的现象称为随机事件。 &4.1 事件与概率 一、事件及其相互关系 (一)事件的意义 1.必然事件 2.不可能事件 3.随机事件

(二)、事件的相互关系 1.和事件 事件A和事件B至少有一个发生,这 一事件称为和事件,记为“A+B”,读 作“或A发生,或B发生
(二)、事件的相互关系 1. 和事件 事件A和事件B至少有一个发生,这 一事件称为和事件,记为“A+B”,读 作“或A发生,或B发生

2.积事件 事件A和事件B同时发生,这一事件 称为积事件,记为“AB”。 3.互斥事件(不相容事件) 事件A和事件B不能同时发生,这 一事件称为互斥事件,记为“A.B=V?
2.积事件 事件A和事件B同时发生,这一事件 称为积事件,记为“AB”。 3.互斥事件(不相容事件) 事件A和事件B不能同时发生,这 一事件称为互斥事件,记为“A.B=V

4.对立事件 若事件A与B是互不相容,且A十B为 必然事件,则称A为B的对立事件。 例如、“产品合格”A和“产品不合 格”B,A+B=必然事件,AB=不可能事 件
4.对立事件 若事件A与B是互不相容,且A+B为 必然事件,则称A为B的对立事件。 例如、“产品合格”A和“产品不合 格”B,A+B=必然事件,AB=不可能事 件

5.完全事件系 若事件A1、A2、A3、A两两互斥, 且每次试验结果必发生其一,则称这 个事件为完全事件系
5.完全事件系 若事件A1、A2、A3、.、An两两互斥, 且每次试验结果必发生其一,则称这n 个事件为完全事件系

6.事件的独立性 若事件A发生与否不影响事件B发生的 可能性,则称事件A和事件B相互独立。 例如花色与产量无关的例
6. 事件的独立性 若事件A发生与否不影响事件B发生的 可能性,则称事件A和事件B相互独立。 例如花色与产量无关的例
二、概率的统计定义及估计方法 表3.1在相同条件下水稻种子发芽试验结果 试验粒数() 510 50100 200 500 1000 发芽粒数(a)584491179 452 901 发芽频率(a/m)1.00.80.880.910.8950.9040.901
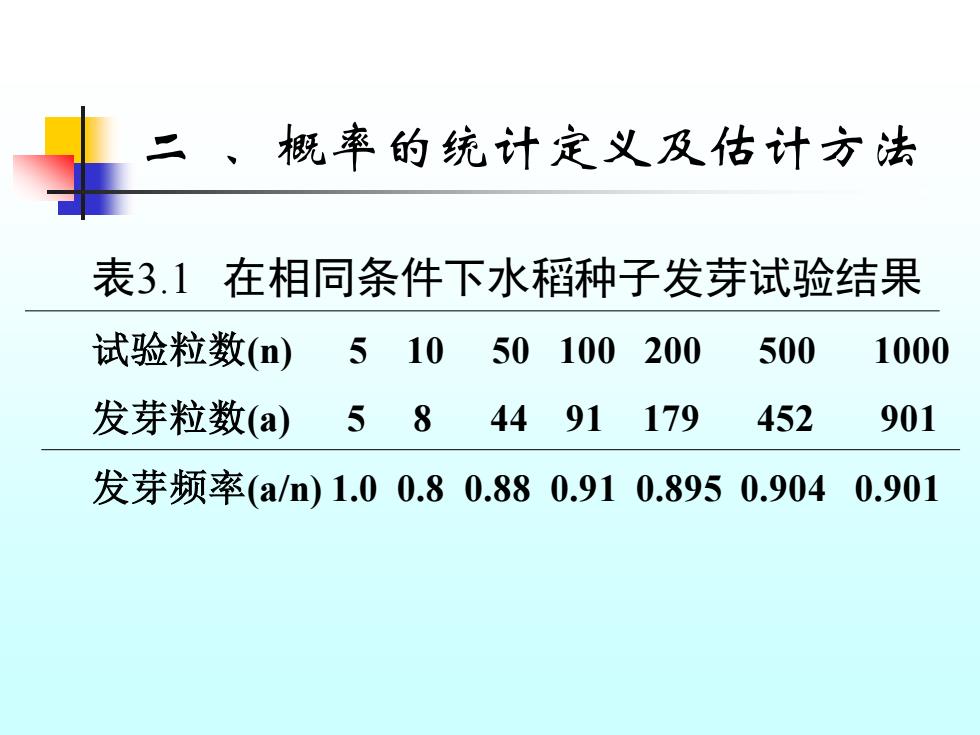
二 、概率的统计定义及估计方法 表3.1 在相同条件下水稻种子发芽试验结果 试验粒数(n) 5 10 50 100 200 500 1000 发芽粒数(a) 5 8 44 91 179 452 901 发芽频率(a/n) 1.0 0.8 0.88 0.91 0.895 0.904 0.901

(一)概率的统计定义 假定在相似条件下重复进行同一类试 验,调查事件A发生的次数a与试验总次数 n的比数称为频率(a/n),则在试验总次数n 逐渐增大时,事件A的频率愈来愈稳定的 接近一个定值P,则定义为事件A发生的 概率记为 P(A)=p=a/n
(一)概率的统计定义 假定在相似条件下重复进行同一类试 验,调查事件A发生的次数a与试验总次数 n的比数称为频率(a/n),则在试验总次数n 逐渐增大时,事件A的频率愈来愈稳定的 接近一个定值P,则定义为事件A发生的 概率.记为 P(A)=p=a/n

概率的基本性质: 1、任何事件的概率都在0与1之间,即: 0≤P(A)≤1 2、必然事件的概率等于1,即: P(U)=1 3、不可能事件的概率等于0,即: PV)=0
概率的基本性质: 3、不可能事件的概率等于0,即: P(V)=0 1、任何事件的概率都在0与1之间,即: 0≤P(A) ≤ 1 2、必然事件的概率等于1,即: P(U)=1