
课堂练习 一、基本统计量计算及区间估计 二、统计假设测验 三、方差分析 四、相关与回归分析
课堂练习 一、基本统计量计算及区间估计 二、统计假设测验 三、方差分析 四、相关与回归分析

一、基本统计量计算及区间估计 用某饮料灌装机灌装的汽水,正常情况下是250l/瓶, 今从中随机抽取10瓶,检验瓶内饮料体积(ml)结果为: 251.5251.0250.8249.0249.5251.5252.5 250.6251.2248.9 (1)试计算其统计量:极差,总和,均值,标准差,方差,平 方和,标准误,变异系数。 (2)求置信度为99%的平均灌装体积的估计区间。 (3)问今天饮料灌装机运转正常否?
一、基本统计量计算及区间估计 1. 用某饮料灌装机灌装的汽水,正常情况下是250ml/瓶, 今从中随机抽取10瓶,检验瓶内饮料体积(ml)结果为: 251.5 251.0 250.8 249.0 249.5 251.5 252.5 250.6 251.2 248.9 (1)试计算其统计量:极差,总和,均值,标准差,方差,平 方和,标准误,变异系数。 (2)求置信度为99%的平均灌装体积的估计区间。 (3)问今天饮料灌装机运转正常否?

二、统计假设测验 1.将14只大白鼠随机分为两组,一组做成白血病模型鼠, 一组为正常鼠,两组鼠脾脏DNA含量(mg/g)如下,请分析 两组鼠表脾脏DNA平均含量是否不同? 白血病组(x1):12.313.213.715.215.415.816.9 正常组(x2):10.811.612.312.713.513.514.8
二、统计假设测验 1. 将14只大白鼠随机分为两组,一组做成白血病模型鼠, 一组为正常鼠,两组鼠脾脏DNA含量(mg/g)如下,请分析 两组鼠表脾脏DNA平均含量是否不同? 白血病组(x1):12.3 13.2 13.7 15.2 15.4 15.8 16.9 正常组(x2): 10.8 11.6 12.3 12.7 13.5 13.5 14.8

2由经验知某零件的重量X~N(u,σ2),=15, σ=0.05;技术革新后,抽出6个零件,测得重量为 (单位:克)14.715.114.815.015.214.6,已 知方差不变,试统计推断,平均重量是否仍为15克? (0=0.05) 解 而样本均值为x=14.9 故U统计量的观测值为 U= x-15 =4.9 0.05/6 因为4.9>1.96,即观测值落在拒绝域内 所以拒绝原假设
2 由经验知某零件的重量X~N(,2),=15, =0.05;技术革新后,抽出6个零件,测得重量为 (单位:克)14.7 15.1 14.8 15.0 15.2 14.6,已 知方差不变,试统计推断,平均重量是否仍为15克? (=0.05) 解 因为4.9>1.96 ,即观测值落在拒绝域内 所以拒绝原假设。 而样本均值为 15 4.9 0.05 6 x U − 故U统计量的观测值为 = = x =14.9

3化工厂用自动包装机包装化肥,每包重量服从正态 分布,额定重量为100公斤。某日开工后,为了确定包 装机这天的工作是否正常,随机抽取9袋化肥,称得平 均重量为99.978,均方差为1.212,能否认为这天的包 装机工作正常?(=0.1) 解而样本均值、均方差为x=99.978,S=1.212 故T统计量的观测值为 T= x-u 99.978-100 =0.0545 1.212/9 因为0.0545<1.86,即观测值落在接受域内 所以接受原假设,即可认为这天的包装机工作正常
解 因为0.0545<1.86 ,即观测值落在接受域内 所以接受原假设,即可认为这天的包装机工作正常。 而样本均值、均方差为 99.978 100 0.0545 1.212 9 x T S n − − = = = 故T统计量的观测值为 x S = = 99.978, 1.212 3 化工厂用自动包装机包装化肥,每包重量服从正态 分布,额定重量为100公斤。某日开工后,为了确定包 装机这天的工作是否正常,随机抽取9袋化肥,称得平 均重量为99.978,均方差为1.212,能否认为这天的包 装机工作正常?(=0.1)
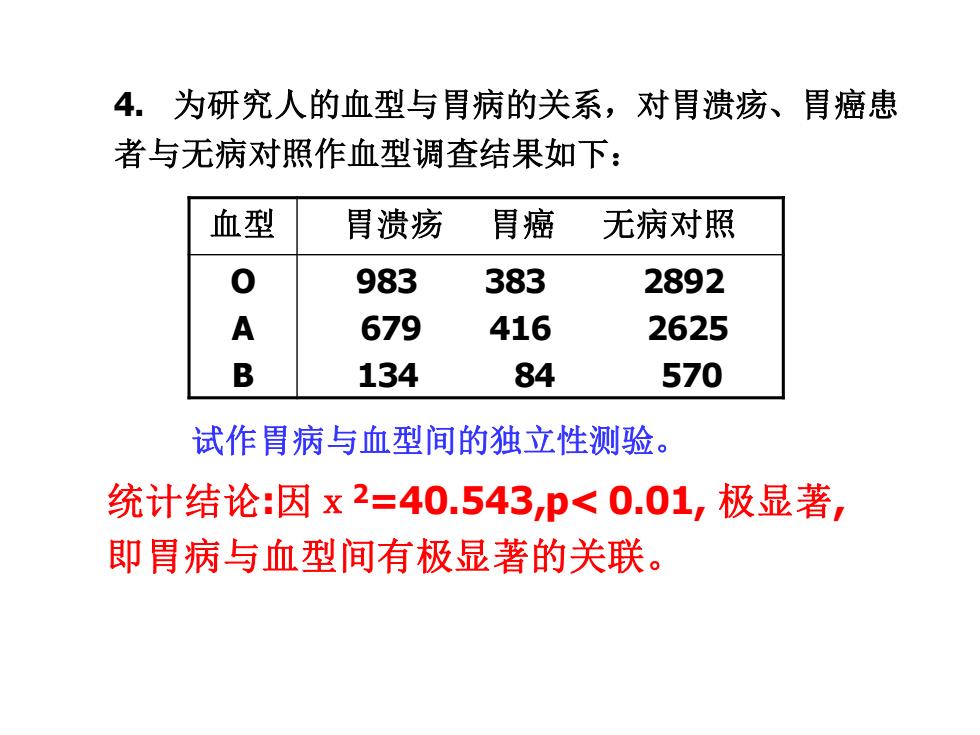
4.为研究人的血型与胃病的关系,对胃溃疡、胃癌患 者与无病对照作血型调查结果如下: 血型 胃溃疡 胃癌 无病对照 0 983 383 2892 A 679 416 2625 B 134 84 570 试作胃病与血型间的独立性测验。 统计结论:因x2=40.543,p<0.01,极显著, 即胃病与血型间有极显著的关联
4. 为研究人的血型与胃病的关系,对胃溃疡、胃癌患 者与无病对照作血型调查结果如下: 血型 胃溃疡 胃癌 无病对照 O A B 983 383 2892 679 416 2625 134 84 570 试作胃病与血型间的独立性测验。 统计结论:因x2=40.543,p< 0.01, 极显著, 即胃病与血型间有极显著的关联

5.有人调查肺癌病人和正常人吸烟情况如下表,试 测定肺癌与吸烟是否有关? 调查总人数 肺癌人数 吸烟 30 17 不吸烟 30 8
5. 有人调查肺癌病人和正常人吸烟情况如下表,试 测定肺癌与吸烟是否有关? 调查总人数 肺癌人数 吸 烟 不吸烟 30 17 30 8

三、方差分析 某5处理效应的比较试验,采用随机区组设计,重复 3次,数据已简化如下表,为可量资料。试做方差分析。 品 种 A B E 区组 I 1 3 1 4 l 2 3 3 1 3 11 1 2 3 1 4 答案
三、方差分析 某5处理效应的比较试验,采用随机区组设计,重复 3次,数据已简化如下表,为可量资料。试做方差分析。 品 种 区组 A B C D E I II III 1 2 1 2 3 2 3 3 3 1 1 1 4 3 4 答案
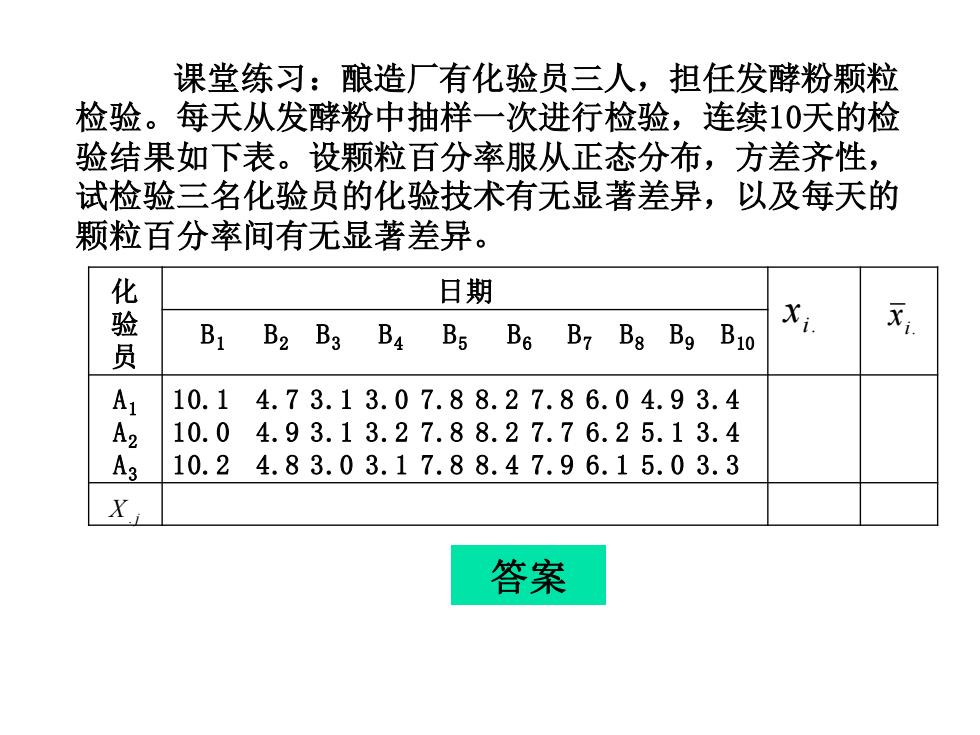
课堂练习:酿造厂有化验员三人,担任发酵粉颗粒 检验。每天从发酵粉中抽样一次进行检验,连续10天的检 验结果如下表。设颗粒百分率服从正态分布,方差齐性, 试检验三名化验员的化验技术有无显著差异,以及每天的 颗粒百分率间有无显著差异。 化 日期 B8 B9 B10 X 员 B1 B2 B3 B4 B5 B6 B7 A1 10.14.73.13.07.88.27.86.04.93.4 A2 10.04.93.13.27.88.27.76.25.13.4 10.24.83.03.17.88.47.96.15.03.3 X 答案
课堂练习:酿造厂有化验员三人,担任发酵粉颗粒 检验。每天从发酵粉中抽样一次进行检验,连续10天的检 验结果如下表。设颗粒百分率服从正态分布,方差齐性, 试检验三名化验员的化验技术有无显著差异,以及每天的 颗粒百分率间有无显著差异。 i. x i. x X. j 化 验 员 日期 B1 B2 B3 B4 B5 B6 B7 B8 B9 B10 A1 A2 A3 10.1 4.7 3.1 3.0 7.8 8.2 7.8 6.0 4.9 3.4 10.0 4.9 3.1 3.2 7.8 8.2 7.7 6.2 5.1 3.4 10.2 4.8 3.0 3.1 7.8 8.4 7.9 6.1 5.0 3.3 答案

课堂练习1: 现有4种食品添加剂(A)对3种不同配方(B)蛋糕质量 的影响试验。每个水平组合含有5个重复,其产品质量评分 结果(略),试分析配方及添加剂对蛋糕质量的影响。 已算出:SS=41.62 SSAB=32.21 SS=7.25SS.=1.56 试完成方差分析表,再写出F测验的统计结论,不要求多重 比较。 课堂练习2:A7A3A A4 A2 Ag A1 a=0.05 作业练习:P3286题要求DF分析
课堂练习1: 现有4种食品添加剂(A)对3种不同配方(B)蛋糕质量 的影响试验。每个水平组合含有5个重复,其产品质量评分 结果(略),试分析配方及添加剂对蛋糕质量的影响。 已算出:SST =41.62 SSAB=32.21 SSA =7.25 SSB =1.56 试完成方差分析表,再写出F测验的统计结论,不要求多重 比较。 作业练习:P328 6题要求DF分析。 课堂练习2:A7 A3 A5 A4 A2 A6 A1 a = 0.05