
6正交试验设计 、 正交试验 正交试验是用正交表(确定试验处理数)来安 排的试验,是复因子试验的一种不完全区组设计方 法,具简单易行,均衡分散、整齐可比的特点。用 较少的处理数获得较好的结果。解决生产中多因子、 多指标、周期长的试验问题。 华南热带农业大学农学院 唐燕琼制
华南热带农业大学农学院 唐燕琼制 6 正交试验设计 一、正交试验 正交试验是用正交表(确定试验处理数)来安 排的试验,是复因子试验的一种不完全区组设计方 法,具简单易行,均衡分散、整齐可比的特点。用 较少的处理数获得较好的结果。解决生产中多因子、 多指标、周期长的试验问题

二、正交表 1.正交表的类型 普通型一一一水平数相等 混合型一一一水平数不全等 水平数:各列的数字数即因子的水平数 L=(Lattice Design=格子设计)表示一张正交表 横行数 (处理组合数) 列数 例:(34 Lk(m) L8(4X24) 水平数 正交表决定从全部处理组合中选哪几个处理组合参加试验
二、正交表 正交表决定从全部处理组合中选哪几个处理组合参加试验。 L=(Lattice Design=格子设计)表示一张正交表 LK (m j ) 横行数 (处理组合数) 列数 水平数 例:L9(34) L8(4×24) 1. 正交表的类型 普通型---水平数相等 混合型---水平数不全等 水平数:各列的数字数即因子的水平数

2、正交表的性质 例:Lg(34) (1)均衡分散、综合可比 L8(4×24) 正交表中: 1.每一列中,不同数字出现的次数相等 2.任意两列中,每种有序数对出现的次数相等 这种性质即正交性,它决定了每个因子各水平的重 复次数相等,并且和个处理组合出现的次数也相等。因 而使得正交设计具有均衡分散、整齐可比的特性。 (2)可伸可缩,效应明确 例如:Lg(34)
2、正交表的性质 (1)均衡分散、综合可比 正交表中: 1.每一列中,不同数字出现的次数相等 2.任意两列中,每种有序数对出现的次数相等 这种性质即正交性,它决定了每个因子各水平的重 复次数相等,并且和个处理组合出现的次数也相等。因 而使得正交设计具有均衡分散、整齐可比的特性。 (2)可伸可缩,效应明确 例如: L9(34) 例:L9(34) L8(4×24)

三、选用正交表设计试验方案的步骤 第一步挑因子、选水平(专业知识) 第二步选一张适合的正交表 所选正交必须符合两个条件: 1.正交表各列的水平数必须等于研究因子水平数 2.正交表自由度≥∑df各因子+∑df各互作 正交表总自由度=横行数一1 **分考察交互作用和不考察交互作用两种情况
三、选用正交表设计试验方案的步骤 第一步 挑因子、选水平(专业知识) 第二步 选一张适合的正交表 所选正交必须符合两个条件: 1.正交表各列的水平数必须等于研究因子水平数 2.正交表自由度≥∑df各因子+∑df各互作 正交表总自由度=横行数-1 **分考察交互作用和不考察交互作用两种情况

第三步 作表头设计,写出试验方案。 将各因子及各项交互作用安排在正交表的列上, 并写出各处理组合。 田间排列可采用随机区组设计或拉丁方设计等。 如试验处理组合数过多,可按某空白列下的水 平号将全部试验处理组合分几个组,每组为1个不完 全区组
第三步 作表头设计,写出试验方案。 将各因子及各项交互作用安排在正交表的列上, 并写出各处理组合。 如试验处理组合数过多,可按某空白列下的水 平号将全部试验处理组合分几个组,每组为1个不完 全区组。 田间排列可采用随机区组设计或拉丁方设计等

四、选用正交表设计试验方案的实例 实例一:不考虑互作 [例13.11]有一小麦栽培试验,A因素为施碳铵方式,4 水平;B因素为追肥时期,2水平;C因素为基肥多少, 2水平;D因素为镇压次数,2水平;E因素为种子处理, 2水平,据以往经验,不存在互作,现要求明确各因素 主效,试予设计
四、选用正交表设计试验方案的实例 [例13.11] 有一小麦栽培试验,A因素为施碳铵方式,4 水平;B因素为追肥时期,2 水平;C因素为基肥多少, 2水平;D因素为镇压次数,2水平;E因素为种子处理, 2 水平,据以往经验,不存在互作,现要求明确各因素 主效,试予设计。 实例一:不考虑互作
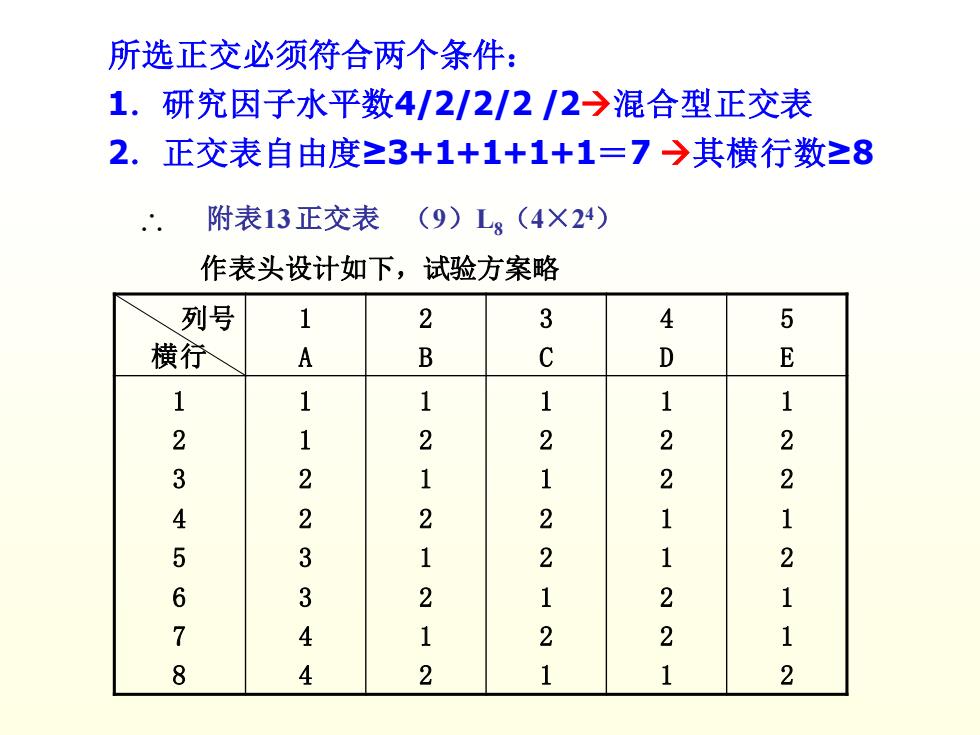
所选正交必须符合两个条件: 1.研究因子水平数4/2/2/2/2→混合型正交表 2.正交表自由度≥3+1+1+1+1=7→其横行数≥8 附表13正交表(9)L8(4×24) 作表头设计如下,试验方案略 列号 1 2 3 4 5 横行 A B C D E 1 1 1 1 1 1 2 1 2 2 2 2 3 2 1 1 2 2 4 2 2 2 1 1 5 3 1 2 1 2 6 3 2 1 2 1 7 4 1 2 2 1 8 4 2 1 1 2
所选正交必须符合两个条件: 1.研究因子水平数4/2/2/2 /2→混合型正交表 2.正交表自由度≥3+1+1+1+1=7 →其横行数≥8 ∴ 附表13 正交表 (9)L8(4×2 4) 列号 横行 1 A 2 B 3 C 4 D 5 E 1 2 3 4 5 6 7 8 1 1 2 2 3 3 4 4 1 2 1 2 1 2 1 2 1 2 1 2 2 1 2 1 1 2 2 1 1 2 2 1 1 2 2 1 2 1 1 2 作表头设计如下,试验方案略

实例二:考虑互作 [例13.12]有一棉花试验,包括品种(A)、施 肥量(B)、打顶期(C)三个因素,每因素皆 取3个水平。现要求通过试验明确各因素的主 效和一级互作,试予设计。 在m=3的正交表中,只有L27(313)可以估计3 个因素的主效(占有3列)和3个一级互作 (占有6列),其表头设计为:
[例13.12] 有一棉花试验,包括品种(A)、施 肥量(B)、打顶期(C)三个因素,每因素皆 取3个水平。现要求通过试验明确各因素的主 效和一级互作,试予设计。 实例二:考虑互作 在m=3的正交表中,只有L27(3 13)可以估计3 个因素的主效(占有3 列)和3个一级互作 (占有6列),其表头设计为:

列号 1 2 3 4 5 6 7 A B AXBAXB C AXC AXC 列号 89 10 111213 BXC BXC 由于一个区组中包含27个处理组合,小区数目太多。 如果分成3个不完全区组,使每一个不完全区组仅包含9个 处理组合,则测验可以更为精确
列号 1 2 3 4 5 6 7 A B A×B A×B C A×C A×C 列号 8 9 10 11 12 13 B×C B×C 由于一个区组中包含27个处理组合,小区数目太多。 如果分成3个不完全区组,使每一个不完全区组仅包含9个 处理组合,则测验可以更为精确

P382(6)L27(313) 例如第9列,排入“区组”,然后依其中1、2、3的水平符号, 将同一水平符号的处理组合归为一个不完全区组,即得如下 的3个不完全区组(在田间布置时各不完全区组及其处理都 要随机排列)的各个处理号为: 不完全区组Ia:1,6,8,12,14,16,20,22,27 不完全区组Ib:2,4,9,10,15,17,21,23,25 不完全区组Ic:3,5,7,11,13,18,19,24,26 如果本试验设置4次重复,则4个重复也可分别用L27 (313) 的9、10、12、13列将各划分成3个不完全组
例如第9 列,排入“区组” ,然后依其中1、2、3的水平符号, 将同一水平符号的处理组合归为一个不完全区组,即得如下 的3个不完全区组(在田间布置时各不完全区组及其处理都 要随机排列)的各个处理号为: 不完全区组I a: 1, 6, 8, 12, 14, 16, 20, 22, 27 不完全区组I b: 2, 4, 9, 10, 15, 17, 21, 23, 25 不完全区组I c: 3, 5, 7, 11, 13, 18, 19, 24, 26 如果本试验设置4次重复,则4个重复也可分别用L27 (3 13) 的9、10、12、13列将各划分成3个不完全组。 P382 (6) L27 (3 13)