章 第四章理论分布与抽样分布 课时 3 &4.1事件与概率 &4.2正态分布 节 &4.3二项分布和泊松分布 &4.4抽样分布 ()了解随机事件、统计概率及其运算,领会小概率事件实际不可能 教学 性原理:(2)了解正态分布、二项分布和泊松分布的概念、基本性质:(3) 目的 掌握样本平均数的抽样分布。 1,二项分布的概念及概率运算: 教学 2.正态分布的特点及其标准化: 重点 3.样本平均数的抽样分布: 教学 突破方法:结合多媒体的形象直观图形及动画过度,使学生更好地理解较 难点 抽象的的概率分布及抽样分布。理解统计意义上的事件概率及应用。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献: 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985 6.《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9.《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10.《食品试验设计与统计分析》,王软德主编,中国农业出版社,2002。 11.《试验设计与分析》,袁志发主编,高等教育出版社,2000
1 章 第四章 理论分布与抽样分布 课时 3 节 &4.1 事件与概率 &4.2 正态分布 &4.3 二项分布和泊松分布 &4.4 抽样分布 教学 目的 (1)了解随机事件、统计概率及其运算,领会小概率事件实际不可能 性原理;(2)了解正态分布、二项分布和泊松分布的概念、基本性质;(3) 掌握样本平均数的抽样分布。 教学 重点 1. 二项分布的概念及概率运算; 2. 正态分布的特点及其标准化; 3.样本平均数的抽样分布; 教学 难点 突破方法:结合多媒体的形象直观图形及动画过度,使学生更好地理解较 抽象的的概率分布及抽样分布。理解统计意义上的事件概率及应用。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献: 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11. 《试验设计与分析》,袁志发主编,高等教育出版社,2000

载学内容正文(含讲课内容、提问设计、课堂练习等) 4.1事件与概率 一、事件及其相互关系 (一)事件的意义 1.必然事件 2.不可能事件 3.随机事件 在一定条件下,可能发生,也可能不发生的现象称为随机事件。 (二)、事件的相互关系 1.和事件 事件A和事件B至少有一个发生,这一事件称为和事件,记为“A+B” 读作“或A发生,或B发生”。 2.积事件 事件A和事件B同时发生,这一事件称为积事件,记为“AB”。 3.互斥事件(不相容事件) 事件A和事件B不能同时发生,这一事件称为互斥事件,记为“A.B=V” 4.对立事件 若事件A与B是互不相容,且A十B为必然事件,则称A为B的对立事件 例如:“产品合格”A和“产品不合格”B,A+B=必然事件,AB=不可能事 过 件。 5.完全事件系 程 若事件A、Aa、A、.、A两两互斥,且每次试验结果必发生其一,则称 这n个事件为完全事件系。 6.事件的独立性 若事件A发生与否不影响事件B发生的可能性,则称事件A和事件B相互 独立。 例如花色与产量无关的, 二、概率的统计定义及估计方法 表3.1在相同条件下水稻种子发芽试验结果 试验粒数(m)510 50 100 200 500 1000 发芽粒数(a)58 4491179 452 901 发芽频率(a/nm)1.00.80.880.910.8950.904 0.901 (一)概率的统计定义 假定在相似条件下重复进行同一类试验,调查事件A发生的次数a与试 验总次数n的比数称为频率(a/n),则在试验总次数n逐渐增大时,事件A的频 率愈来愈稳定的接近一个定值P,则定义为事件A发生的概率.记为P(A) p=a/n
2 教 学 过 程 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &4.1 事件与概率 一、事件及其相互关系 (一)事件的意义 1.必然事件 2.不可能事件 3.随机事件 在一定条件下,可能发生,也可能不发生的现象称为随机事件。 (二)、事件的相互关系 1.和事件 事件 A 和事件 B 至少有一个发生,这一事件称为和事件,记为“A+B”, 读作“或 A 发生,或 B 发生”。 2.积事件 事件 A 和事件 B 同时发生,这一事件称为积事件,记为“AB”。 3.互斥事件(不相容事件) 事件 A 和事件 B 不能同时发生,这一事件称为互斥事件,记为“A.B=V” 4.对立事件 若事件A与B是互不相容,且A+B为必然事件,则称A为B的对立事件。 例如:“产品合格”A 和“产品不合格”B,A+B=必然事件,AB=不可能事 件。 5.完全事件系 若事件 A1、A2、A3、.、An 两两互斥,且每次试验结果必发生其一,则称 这 n 个事件为完全事件系。 6.事件的独立性 若事件 A 发生与否不影响事件 B 发生的可能性,则称事件 A 和事件 B 相互 独立。 例如花色与产量无关的。 二 、概率的统计定义及估计方法 表 3.1 在相同条件下水稻种子发芽试验结果 试验粒数(n) 5 10 50 100 200 500 1000 发芽粒数(a) 5 8 44 91 179 452 901 发芽频率(a/n) 1.0 0.8 0.88 0.91 0.895 0.904 0.901 (一)概率的统计定义 假定在相似条件下重复进行同一类试验,调查事件 A 发生的次数 a 与试 验总次数 n 的比数称为频率(a/n),则在试验总次数 n 逐渐增大时,事件 A 的频 率愈来愈稳定的接近一个定值 P,则定义为事件 A 发生的概率.记为 P(A)= p=a/n

概率的基本性质: 1、任何事件的概率都在0与1之间,即:0≤P(A)≤1 2、以然車件的概率等干1即: PU)=1 3、不可能事件的概率等于0,即: P(W)=0 (二)概率的运算方法 1.加法定理 两个互斥事件A和B的和事件的概率等于事件A和事件B各自的概率之和 既:P(A+B)=P(A)+P(B) 例如有一批种子,其中二级占5%,一级占10%,其余为三级,问三级种子 占多少? 2.乘法定理 两个独立事件A和B的积事件的概率等于事件A和事件B各自概率的乘积, 即:P(AXB)=P(A)XP(B) 若一批玉米种子发芽率为0.9,发芽后能出士的概率为0.8,求这批种子的 出苗率? P(A×B)=P(A)×P(B)=0.9×0.8=0.72 3.对立事件的概率 若事件A的概率为P(A),那么对立事件的概率为:P(A)=1-P() 学 若一批种子发芽率为0.9,则不发芽率的概率为1-0.9=0.1 4.完全事件系的概率 若有几个事件AL,A2,.,A如是试验的完全事件系,则这些事件的概率之 和为1。 即:P(A1+A2+.+An) =P(A1)+P(A2)+.+(An) 1 一批棉花纤维长度<28cm事件A1,概率为0.2:28-30cm事件A2,概率为 0.6:)30cm事件A3,概率为0.2;这三种情况构成一个完全事件系,其概率之 和为: P(A1+A2+A3)=P(A1)+P(A2)+P(A3)=0.2+0.6+0.2=1 三.小概率事件实际不可能性 随机事件概率的大小客观地反映事件在一次试验中发生的可能性的大小 概率大表示该事件发生的可能性大:概率小,说明该事件发生的可能性小: 农业研究中多采用5%、1%这两个标准作为小概率事件
3 教 学 过 程 概率的基本性质: 1、任何事件的概率都在 0 与 1 之间,即: 0≤P(A) ≤ 1 2、必然事件的概率等于 1,即: P(U)=1 3、不可能事件的概率等于 0,即: P(V)=0 (二)概率的运算方法 1.加法定理 两个互斥事件A和 B的和事件的概率等于事件 A和事件B各自的概率之和, 既:P(A+B)=P(A)+P(B) 例如 有一批种子,其中二级占 5%,一级占 10%,其余为三级,问三级种子 占多少? 2.乘法定理 两个独立事件A和 B的积事件的概率等于事件 A和事件B各自概率的乘积, 即: P(A×B)=P(A)×P(B) 若一批玉米种子发芽率为 0.9,发芽后能出土的概率为 0.8,求这批种子的 出苗率? P(A×B)=P(A) ×P(B)=0.9×0.8=0.72 3.对立事件的概率 若事件 A 的概率为 P(A),那么对立事件的概率 为: P( A )=1-P(A) 若一批种子发芽率为 0.9,则不发芽率的概率为 1-0.9=0.1 4.完全事件系的概率 若有几个事件 A1,A2,.,An 是试验的完全事件系,则这些事件的概率之 和为 1。 即:P(A1+A2+. + An) =P(A1)+P(A2) + . +(An) =1 一批棉花纤维长度30cm 事件 A3,概率为 0.2;这三种情况构成一个完全事件系,其概率之 和为: P(A1+A2+A3)=P(A1)+P(A2)+P(A3)=0.2+0.6+0.2=1 三. 小概率事件实际不可能性 随机事件概率的大小客观地反映事件在一次试验中发生的可能性的大小。 概率大表示该事件发生的可能性大;概率小,说明该事件发生的可能性小; 农业研究中多采用 5%、1%这两个标准作为小概率事件
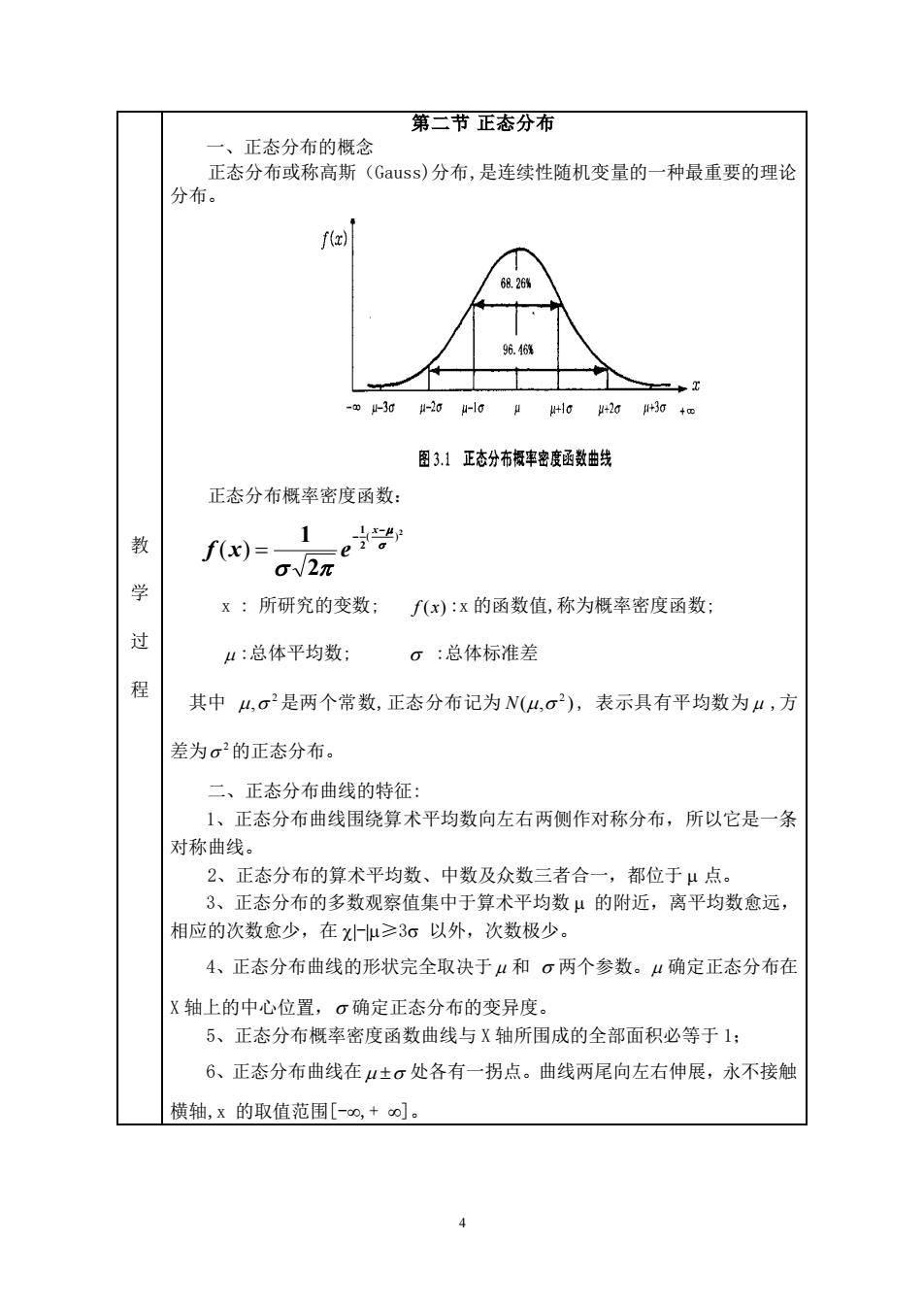
第二节正态分布 一、正态分布的概念 正态分布或称高斯(Gauss)分布,是连续性随机变量的一种最重要的理论 分布 030-20-00H6=26m0+m 图3.1正态分布摄率密度函数曲线 正态分布概率密度函数: 教 f(x)= X:所研究的变数: f(x):x的函数值,称为概率密度函数 4:总体平均数: 。:总体标准差 其中4,σ2是两个常数,正态分布记为N(4,σ2),表示具有平均数为4,方 差为σ2的正态分布。 二、正态分布曲线的特征: 1、正态分布曲线围绕算术平均数向左右两侧作对称分布,所以它是一条 对称曲线。 2、正态分布的算术平均数、中数及众数三者合一,都位于μ点。 3、正态分布的多数观察值集中于算术平均数μ的附近,离平均数愈远, 相应的次数愈少,在u≥3σ以外,次数极少。 4、正态分布曲线的形状完全取决于“和。两个参数。“确定正态分布在 X轴上的中心位置,。确定正态分布的变异度。 5、正态分布概率密度函数曲线与X轴所围成的全部面积必等于1: 6、正态分布曲线在μ±。处各有一拐点。曲线两尾向左右伸展,永不接能 横轴,x的取值范围[-0,+o
4 教 学 过 程 第二节 正态分布 一、正态分布的概念 正态分布或称高斯(Gauss)分布,是连续性随机变量的一种最重要的理论 分布。 正态分布概率密度函数: x : 所研究的变数; f (x) :x 的函数值,称为概率密度函数; :总体平均数; :总体标准差 其中 2 , 是两个常数,正态分布记为 ( , ) 2 N , 表示具有平均数为 ,方 差为 2 的正态分布。 二、正态分布曲线的特征: 1、正态分布曲线围绕算术平均数向左右两侧作对称分布,所以它是一条 对称曲线。 2、正态分布的算术平均数、中数及众数三者合一,都位于 点。 3、正态分布的多数观察值集中于算术平均数 的附近,离平均数愈远, 相应的次数愈少,在 -≥3 以外,次数极少。 4、正态分布曲线的形状完全取决于 和 两个参数。 确定正态分布在 X 轴上的中心位置, 确定正态分布的变异度。 5、正态分布概率密度函数曲线与 X 轴所围成的全部面积必等于 1; 6、正态分布曲线在 处各有一拐点。曲线两尾向左右伸展,永不接触 横轴,x 的取值范围[-,+ ]。 2 2 1 2 1 ( ) ( ) − − = x f x e
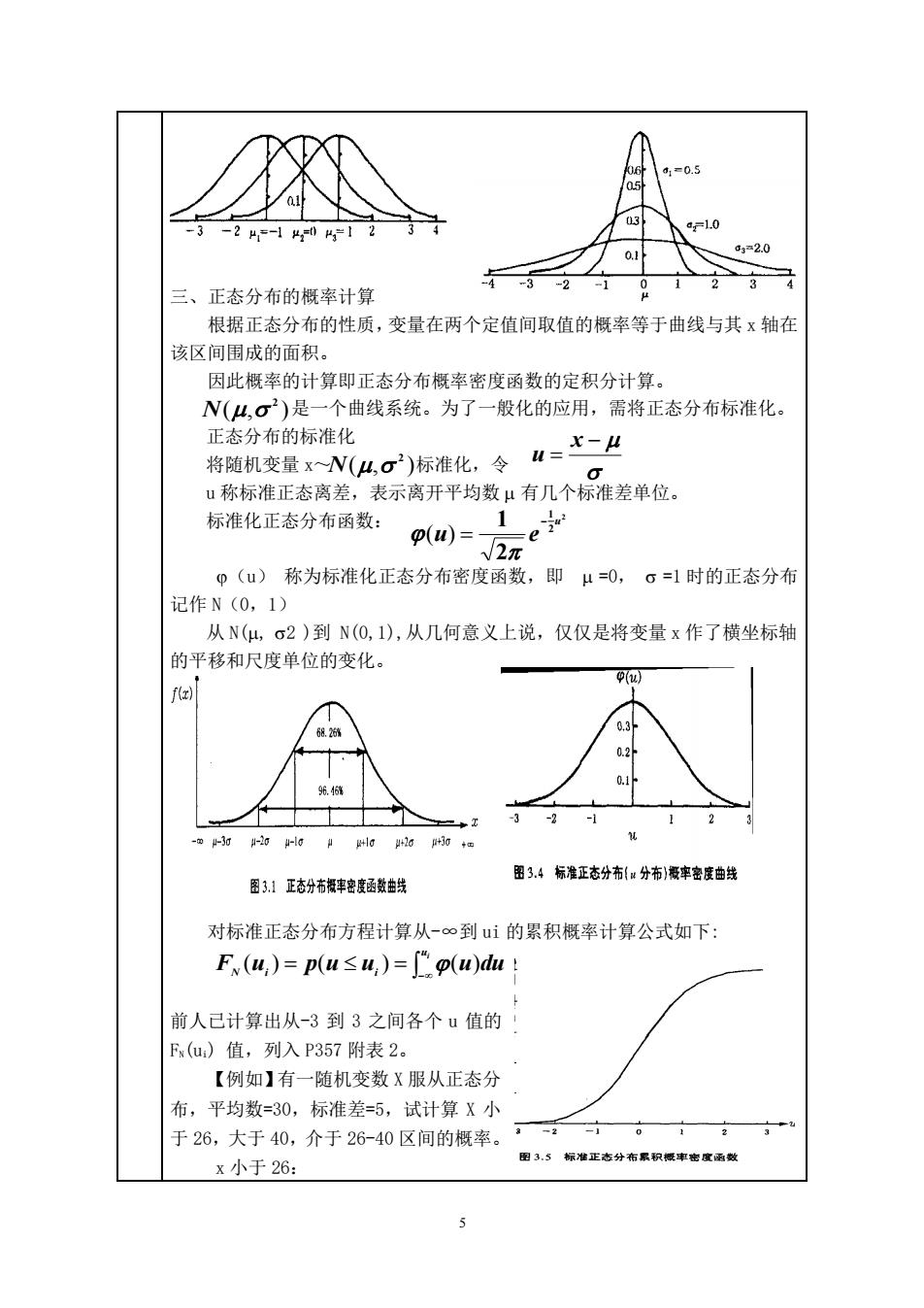
0 3 24,104】2 c1=2.0 82 正态分布的概率计算 根据正态分布的性质,变量在两个定值间取值的概率等于曲线与其x轴在 该区间围成的面积。 因此概率的计算即正态分布概率密度函数的定积分计算。 N(4,σ)是一个曲线系统。为了一般化的应用,需将正态分布标准化。 指随机变豆V(以g)标准化,令u=二业 正态分布的标准化 "称标准正态离差,表示离开平均数4有几个标准差单位。 标准化正态分布函数: p(W)= 2元 p(u)称为标准化正态分布密度函数,即μ=0,。=1时的正态分布 记作N(0,1) 从N(μ,σ2)到N(O,1),从几何意义上说,仅仅是将变量x作了横坐标轴 的平移和尺度单位的变化。 2 图3.1正疮分右丰密度超数出线 图3.4标准正态分(分右制薇率密度色线 对标准正态分布方程计算从-∞到ui的累积概率计算公式如下: Fw(u,)=p(u≤4,)=rp(w)du 前人己计算出从-3到3之间各个山值的 F,(u)值,列入P357附表2。 【例如】有一随机变数X服从正态分 布,平均数=30,标准差=5,试计算X小 26,大于40,介于26-40区间的概率。 第2 x小于26: 图3,5标准正志分佑累积概率密度函数
5 三、正态分布的概率计算 根据正态分布的性质,变量在两个定值间取值的概率等于曲线与其 x 轴在 该区间围成的面积。 因此概率的计算即正态分布概率密度函数的定积分计算。 是一个曲线系统。为了一般化的应用,需将正态分布标准化。 正态分布的标准化 将随机变量 x~ 标准化,令 u 称标准正态离差,表示离开平均数 有几个标准差单位。 标准化正态分布函数: (u) 称为标准化正态分布密度函数,即 =0, =1 时的正态分布 记作 N(0,1) 从 N(, 2 )到 N(0,1),从几何意义上说,仅仅是将变量 x 作了横坐标轴 的平移和尺度单位的变化。 对标准正态分布方程计算从-∞到 ui 的累积概率计算公式如下: 前人已计算出从-3 到 3 之间各个 u 值的 FN(ui) 值,列入 P357 附表 2。 【例如】有一随机变数 X 服从正态分 布,平均数=30,标准差=5,试计算 X 小 于 26,大于 40,介于 26-40 区间的概率。 x 小于 26: 2 2 1 2 1 u u e − = ( ) − = x u ( , ) 2 N ( , ) 2 N − = = ui FN (ui ) p(u ui ) (u)du

4==4=26-30/5=-0.8 查附表1,八x≤26)=以u≤-0.8=0219 大于40: u=X-H =(40-30)/5=2 6 查表1,F(u=2)=0.9773则 p(x≥40)=1-p(x<40)=1-0.9773=0.0227 x介于26与40之间: p(26≤x≤40)=p(-0.8≤u≤2)=Fu=2)-F(u=-0.8) =0.9773-0.2119 (u) P.0219 P0.973#- 教 学 P=.7654 μ=0 +20 0.02 图3.6概率计算示图 附表2列出的就是两尾概率。 0,025 0.95 0.025 0.005 0.99 0005 3-1.96-1011.963 -2.58-101 2.58 图3.7两尾概率图示
6 教 学 过 程 − = x u =(26-30)/5= -0.8 查附表 1, 大于 40: =(40-30)/5=2 查表 1, F(u=2)=0.9773 则 x 介于 26 与 40 之间: 附表 2 列出的就是两尾概率。 p(x 26) = p(u −0.8)= 0.2119 p(x 40) = 1− p(x 40) = 1− 0.9773 = 0.0227 − = x u 0 9773 0 2119 26 40 0 8 2 2 0 8 . . ( ) ( . ) ( ) ( . ) = − p x = p − u = F u = − F u = −

第三节二项分布和泊松分布 一、二项总体与二项分布 在独立重复试验中,总体的某个性状每一次试验只有非此即彼两个可能结 果,这种非此即彼事件所构成的总体叫二项总体,也叫0,1总体。 当每次独立的从二项总体抽取n个个体,这n个个体:“此”事件出现的 次数X可能有0、1、2、.n,共有n+1种,这n+1种可能性有它各自的概率, 组成一个分布,此分布叫二项概率分布或简称二项分布。二项分布是一种离散 型分布。 例如,观察玉米播种后的出苗数,出苗记为“此”事件,概率为p:不出 苗记为彼事件,概率为q。 若每窝播种5粒种子,则对每窝出苗情况的观察结果会有如下几种可能: X: 0 1 A P(0) P(1) P(2) P(3)P(4) P(5) 由这6种情况的相应概率组成的分布,就是=5时出苗数的二项分布。 二、二项分布的概率计算 1、二项分布的定义: 假定某事件发生的概率为p,不发生的概率为q,则做n次独立性试验, 学 发生k(0≤k≤)次的概率为: 过 P.(k)=Cpg-t,k=01,2,n 则随机变量X服从参数为n和p的二项分布,记为X一B(m,p). 2.二项分布的特点: 具有概率分布的一切性质: (1)P(x=k)=n(k)≥0 二项分布概率之和等于1 pk≤m-=n.&≤m-三cpg ④pl≥m=p.k≤m=cpg (5)p(m sxsm2)=p,(msksm )=chp'q"k (msm2) (p+q)°=Cpq"+Cp'q"+.+Cpq+.+Cpq 3.二项总体的参数 对于一个给定的二项分布,和p是常数。二项总体的平均数、方差和标 准差的计算公式如下: 4=∑p(xi)xi 4=p c2=p4 o2=∑p(xi)(xi-4) g=√np网
7 教 学 过 程 第三节 二项分布和泊松分布 一、二项总体与二项分布 在独立重复试验中,总体的某个性状每一次试验只有非此即彼两个可能结 果,这种非此即彼事件所构成的总体叫二项总体,也叫 0,1 总体。 当每次独立的从二项总体抽取 n 个个体,这 n 个个体:“此”事件出现的 次数 X 可能有 0、1、2、.n,共有 n+1 种,这 n+1 种可能性有它各自的概率, 组成一个分布,此分布叫二项概率分布或简称二项分布。二项分布是一种离散 型分布。 例如,观察玉米播种后的出苗数,出苗记为“此”事件,概率为 p;不出 苗记为彼事件,概率为 q。 若每窝播种 5 粒种子,则对每窝出苗情况的观察结果会有如下几种可能: X : 0 1 2 3 4 5 P: P(0) P(1) P(2) P(3) P(4) P(5) 由这 6 种情况的相应概率组成的分布,就是 n=5 时出苗数的二项分布。 二、二项分布的概率计算 1、二项分布的定义: 假定某事件发生的概率为 p,不发生的概率为 q,则做 n 次独立性试验, 发生 k (0≤k≤n)次的概率为: P k C p q k n k k n k n n ( ) = , = 0,1,2,., − 则随机变量 X 服从参数为 n 和 p 的二项分布,记为 X~B(n,p). 2. 二项分布的特点: 具有概率分布的一切性质: (1) P(x=k)=Pn(k)≥0 (2) 二项分布概率之和等于 1 ( ) ( ) k n k m k k p x m pn k m cn p q − = = = 0 (3) ( ) ( ) k n k n k m k p x m pn k m cn p q − = (4) = = ( ) ( ) ( ) 1 2 1 2 1 2 2 1 (5) p m x m p m k m c p q m m k n k m k m k = n = n − = 3.二项总体的参数 对于一个给定的二项分布,n 和 p 是常数。二项总体的平均数、方差和标 准差的计算公式如下: 0 0 1 1 1 0 p q C p q C p q C p q C p q n n n i i n i n n n n n n + = + + + + + ( ) − − npq npq np = = = 2 = − = 2 2 ( )( ) ( ) p xi xi p xi xi

μ表示做n次独立试验,某事件平均出现的次数为np次 σ表示X取值的离散度或变异大小 【例如】有一批玉米种子,其发芽率为70%,如每窝播种4粒,问出苗数 为2和3时的概率分别为多少? (g+p)=Copg'+Cip'g+Cipg+Cip'g+Cip'g 出苗数为2概率: Cp2g2=6x0.72x0.32=0.2646 出苗率为3概率: Cp2g=4×0.7x0.3=0.4116 三、泊松分布 二项总体中稀有事件的概率分布不呈二项分布,而是遵从另一种理论分布 泊松分布(poisson distribution)) 1、统计定义 若变量x服从二项分布,当P很小,n一∞且np=m为一常数时,该二项分 布的极限为泊松分布。 2、概率函数 过 p(x)= 其中m=np,e=2.71828 程 x=01,2,0 普阿松分布的平均数和方差都等于常数m,即:=σ2=m,。=√m 3.泊松分布的概率计算(不要求,不讲) 泊松分布是一个偏斜分布,但随着m的增大,分布渐趋对称,接近正态 分布。通常当m大于50时,可用正态分布来处理泊松分布的问题
8 教 学 过 程 μ表示做n次独立试验,某事件平均出现的次数为np次 表示X取值的离散度或变异大小 【例如】有一批玉米种子,其发芽率为 70%,如每窝播种 4 粒,问出苗数 为 2 和 3 时的概率分别为多少? 三、泊松分布 二项总体中稀有事件的概率分布不呈二项分布,而是遵从另一种理论分布 ——泊松分布(poisson distribution) 1、统计定义 若变量 x 服从二项分布,当 P 很小,n→∞且 np=m 为一常数时,该二项分 布的极限为泊松分布。 2、概率函数 = = − 0,1,2., ! ( ) x e x m p x m x 其中 m=np, e=2.71828 普阿松分布的平均数和方差都等于常数 m,即: = = m, = m 2 3.泊松分布的概率计算(不要求,不讲) 泊松分布是一个偏斜分布,但随着 m 的增大,分布渐趋对称,接近正态 分布。通常当 m 大于 50 时,可用正态分布来处理泊松分布的问题。 4 0.7 0.3 0.4116 3 6 0.7 0.3 0.2646 2 ( ) 3 3 1 3 1 4 2 2 2 2 2 4 4 4 0 4 3 3 1 4 2 2 2 4 1 1 3 4 0 0 4 4 4 = = = = + = + + + + C p q C p q q p C p q C p q C p q C p q C p q 出苗率为 概率: 出苗数为 概率:

第四节抽样分布 统计学:1、总体· 样本 抽样分布 2、样本 总体 统计推断 一、正态总体的抽样分布 从总体到样本,就是研究抽样分布的问题: 从样本到总体,这就是统计推断问题: (一)样本平均数的抽样分布 从X~N(4,σ2)中抽取的随机样本X1,.,n,它产生了灭,S2等统计量, 这些统计量的分布显然与总体有关。由于X1,.,X和相互独立,且均服从 X~N(4,σ2),又正态分布变量的线性组合仍服从正态分布,因而 xN(4,21 因此抽样分布u==尖 N(0,) 2末知时:1=1-)(服从自由度为n1的分布) sl√n 教 这个分布可以推断己知的4。与μ的差异问题及μ的估计问题。 t分布曲线特点:1. 单峰曲线 2.左右对称(t=0) 3· 曲线图形由自由度不同而不同 过 4.t—〉±∞f(t)-〉0 -)∞t分布与标准正态分布曲线一致 5.曲线与横坐标所不便夹的面积等于1(100%) (仁)两个独立样本平均数差数无-元,的分布 %属)=0 )nn u=国-)-(44)_G-)-44 + n n2 二、二项总体的抽样分布 局部局限定理:变数X服从二项分布,则做N次独立试验,X的总体均数μ np,总体变量6-nPq,当)50,P不太靠近0或1时 户-产服从~ n 其中其中:G。=√p1-p)/n 当资料用次数进行假设检验。《=功吧
9 教 学 过 程 第四节 抽样分布 统计学:1、总体 → 样本 → 抽样分布 2、样本 → 总体 → 统计推断 一、正态总体的抽样分布 从总体到样本,就是研究抽样分布的问题; 从样本到总体,这就是统计推断问题; (一)样本平均数的抽样分布 从 ~ ( , ) 2 X N 中抽取的随机样本 X1,.,Xn,它产生了 2 X, S 等统计量, 这些统计量的分布显然与总体有关。由于 X1,.,Xn 相互独立,且均服从 ~ ( , ) 2 X N ,又正态分 布 变 量 的 线 性 组 合 仍 服 从 正 态 分 布 , 因 而 ~ ( , / ) 2 X N n 。 因此抽样分布 (0,1) / N n x u − = 2末知时 : ~ ( 1) / − − = t n s n x t (服从自由度为 n-1 的 t 分布) 这个分布可以推断已知的 0 与 的差异问题及 的估计问题。 t 分布曲线特点:1.单峰曲线 2.左右对称(t=0) 3.曲线图形由自由度不同而不同 4.t──〉±∞ f(t)──〉0 n──〉∞ t分布与标准正态分布曲线一致 5.曲线与横坐标所不便夹的面积等于 1(100%) (二)两个独立样本平均数差数 1 2 x − x 的分布 ( ) 0 1 2 x −x = 2 2 2 1 2 1 ( ) 1 2 n n x x − = + u= 2 2 2 1 2 1 1 2 1 2 ( ) 1 2 1 2 ( ) ( - ) ( ) ( - ) 1 2 n n x x x x x x + − − = − − − 二、二项总体的抽样分布 局部局限定理: 变数 X 服从二项分布,则做 N 次独立试验,X 的总体均数μ= np,总体变量δ2=npq,当 N〉50,P不太靠近0或1时 n x p ˆ = 服从 ˆ ~ ( , ) n pq p N p p p p u ˆ ˆ ˆ − = 其中 其中: ˆ pˆ = p(1− p ) / n 当资料用次数进行假设检验。 np np np u ˆ ˆ ˆ − =

三、总结与巩固 1.小结 本章内容抽象理论性强,同学们只掌握抽样分布及统计意义概率。 )二项分布的计算 2)标准正态分布N(O,1)的转化 3)抽样分布又~N(4,c21m): G): 玉-~N4-m 2.考核知识点 二项分布、正态分布的符合表示。 3.考核要求 了解理论分布与抽样分布及概率计算,对统计推断的原理及其应用的掌握 起关键作用,但无须会推导公式,只要理解抽样分析的公式来源,以便学好第 5章的应用。 通过多媒体的形象直观图形及动画过程,使学生更好地了解较抽象的的概 率分 布及袖样分布 本章内容抽象学 定困难 今后本 要老 用直观的三维动画图形,提前举一简单应用,有助于理解效果可能会更好
10 三、总结与巩固 1.小结 本章内容抽象理论性强,同学们只掌握抽样分布及统计意义概率。 1)二项分布的计算 2)标准正态分布 N(0,1)的转化 3) 抽样分布 ~ ( , / ) 2 X N n ; ~ ( , ) 2 2 2 1 2 1 1 2 1 2 n n x x N − − + ; n x p ˆ = , ˆ ~ ( , ) n pq p N p 2.考核知识点 二项分布、正态分布的符合表示。 3.考核要求 了解理论分布与抽样分布及概率计算,对统计推断的原理及其应用的掌握 起关键作用,但无须会推导公式,只要理解抽样分析的公式来源,以便学好第 5 章的应用。 教 学 后 记 通过多媒体的形象直观图形及动画过程,使学生更好地了解较抽象的的概 率分布及抽样分布。本章内容抽象学生理解有一定困难。今后本章教学中要多 用直观的三维动画图形,提前举一简单应用,有助于理解效果可能会更好