
第九章 多因素试验结果的分析 &9.1 复因子试验概述 &9.2二因素随机区组设计的结果分析 &9.3 二因素裂区设计的结果分析 &9.4正交试验设计及统计分析 团 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 第九章 多因素试验结果的分析 &9.1 复因子试验概述 &9.2 二因素随机区组设计的结果分析 &9.3 二因素裂区设计的结果分析 &9.4 正交试验设计及统计分析

&9.1复因子试验概述 一、复因子试验的必要性 不仅能解决各因子水平间的比较问题,且 能分析因子间的互作问题。 >与同条件下的单因子试验精确度高 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 &9.1 复因子试验概述 一、复因子试验的必要性 ➢ 不仅能解决各因子水平间的比较问题,且 能分析因子间的互作问题。 ➢ 与同条件下的单因子试验精确度高

二、单、复因子试验方差分析不同点 1.必须将处理组合的SS和DF进一步分解为各个因 子及其各项交互作用的SS和DF,从而进行因子主效 应及交互作用效应的F测验。 2.要用二项表来计算各因子及各项交互作用的平 方和
二、单、复因子试验方差分析不同点 1.必须将处理组合的SS和DF进一步分解为各个因 子及其各项交互作用的SS和DF,从而进行因子主效 应及交互作用效应的F测验。 2.要用二项表来计算各因子及各项交互作用的平 方和

例如:2×4复因子试验,试作自由度分析。 (1)采用完全随机排列设计,重复3次 (2)采用随机区组设计,重复3次 (3)采用拉丁方设计 课堂练习: 2×3×4复因子试验,采用随机区组设计, 重复3次,试作自由度分析
例如:2×4复因子试验,试作自由度分析。 (1)采用完全随机排列设计,重复3次 (2)采用随机区组设计,重复3次 (3)采用拉丁方设计 课堂练习: 2×3×4复因子试验,采用随机区组设计, 重复3次,试作自由度分析

&9.2二因素随机区组设计的结果分析 、二因素随机区组试验的线性模型和期望均方 设有A、B两个试验因素,A因素有a个水 平,B因素有b个水平,采用随机区组设计,重 复r次。共有ab个水平组合,每一个水平组合 有r个观察值。则该试验共有rab个观察值。 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 &9.2 二因素随机区组设计的结果分析 一、二因素随机区组试验的线性模型和期望均方 设有A、B两个试验因素,A因素有a个水 平,B因素有b个水平 , 采用随机区组设计,重 复r次。共有ab个水平组合,每一个水平组合 有r个观察值。则该试验共有rab个观察值
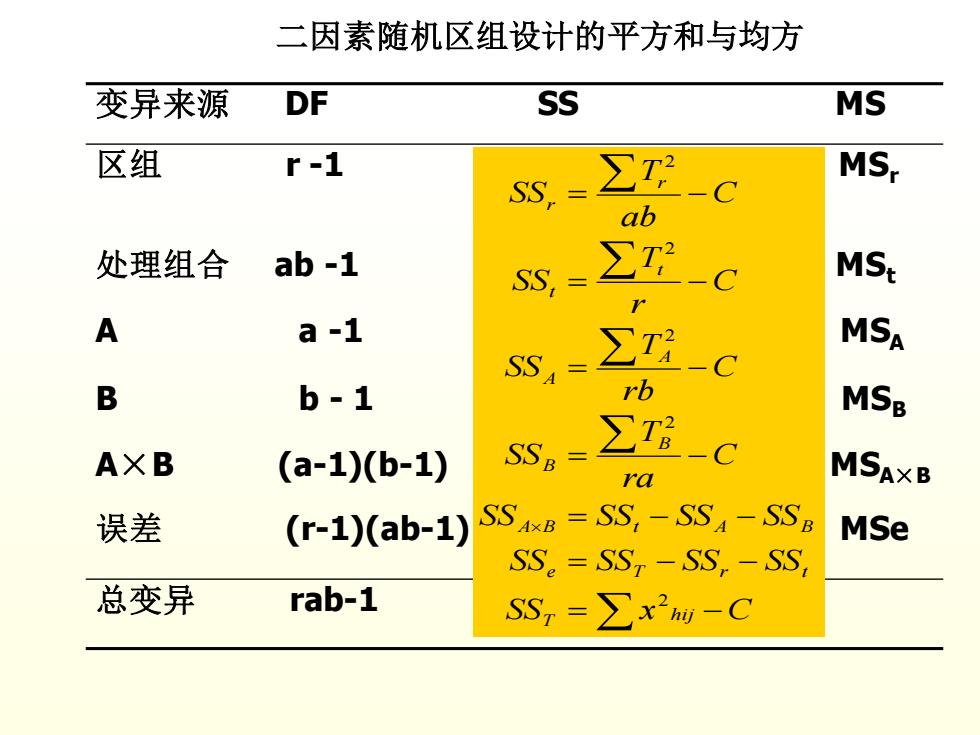
二因素随机区组设计的平方和与均方 变异来源 DF SS MS 区组 r-1 ∑ C MSr ab 处理组合 ab-1 SS ∑T -C MSt A a-1 ∑ MSA SSA A -C B b-1 rb MSB ∑Ta AXB (a-1)b-1) SSB -C ra MSAXB 误差 (r-1)(ab-1) SS4xB =SS-SSA-SSB MSe SS。=SSr-SS,-SS, 总变异 rab-1 SS=∑x2M-C
二因素随机区组设计的平方和与均方 变异来源 DF SS MS 区组 r -1 MSr 处理组合 ab -1 MSt A a -1 MSA B b - 1 MSB A×B (a-1)(b-1) MSA×B 误差 (r-1)(ab-1) MSe 总变异 rab-1 SS x C SS SS SS SS SS SS SS SS C ra T SS C rb T SS C r T SS C ab T SS hij T e T r t A B t A B B B A A t t r r = − = − − = − − = − = − = − = − 2 2 2 2 2

二因素随机区组的期望均方 变异 期望均方 来源 固定模型 随机模型 区组 o2e+abr2B σ2e+abo2B A G 2+rbk2 G2e+ro(x+rbo2 B G2+rak2g 2。+ro2A×B+rao2B AXB c2et rK2(AXB) c2e+roaXB 误差 o2e c2e
变异 期望均方 来源 固定模型 随机模型 区组 σ 2e+abκ2 β σ 2e+abσ2 β A σ 2 e+rbκ2 A σ 2e+rσ2 (A×B) +rbσ2 A B σ 2 e + raκ2 B σ 2 e+rσ2 (A×B) +raσ2 B A×B σ 2e+ rκ2 (A×B) σ 2e+rσ2 A×B 误差 σ 2e σ 2e 二因素随机区组的期望均方

对固定模型来说: F被测项 MS被测项 MS。 但对随机模型来说,区组变异和互作变异用误 差均方进行F测验;而A、B的变异则应用互作项的 均方进行F测验
对固定模型来说: 但对随机模型来说,区组变异和互作变异用误 差均方进行F测验;而A 、B的变异则应用互作项的 均方进行F测验。 e MS F MS 被测项 被测项 =

二因素随机区组与单因素随机区组的差别: 二因素试验的处理项可以再分解为A因素水平间、 B因素水平间和AB互作三部分: SSt=SSA+SSB+SSAXB (ab-1)=(a-1)+(b-1)+(a-1)b-1) 其中,SSt为处理平方和;SSA×B为互作项平 方和;SSA为A因素平方和;SSB为B因素平方和
二因素随机区组与单因素随机区组的差别: 二因素试验的处理项可以再分解为A因素水平间、 B因素水平间和AB互作三部分: SSt = SSA + SSB + SSA×B (ab-1)=(a-1)+(b-1)+(a-1)(b-1) 其中,SSt 为处理平方和;SSA×B 为互作项平 方和 ;SSA为A因素平方和; SSB为B因素平方和

SAS另例 二、二因素随机区组试验分析实例 [例9.1]橡胶树品系A与栽培密度B试验,采用随 机区组设计重复4次,测得小区年干胶产量如下 表,试作方差分析。 处理组合 A A2 区组和 区组 B1 B2 B3 B1 B2 B3 区组1 56 60 66 65 60 53 360 区组2 45 50 57 61 58 53 324 区组3 43 45 50 60 56 48 302 区组4 46 48 50 63 60 55 322 处理总和 190 203 223 249 234 209 T=1308
[例9.1]橡胶树品系A与栽培密度B试验,采用随 机区组设计重复4次,测得小区年干胶产量如下 表,试作方差分析。 处理组合 区组 A1 A2 B1 B2 B3 B1 B2 B3 区组1 56 60 66 65 60 53 区组2 45 50 57 61 58 53 区组3 43 45 50 60 56 48 区组4 46 48 50 63 60 55 处理总和 190 203 223 249 234 209 区组和 360 324 302 322 T=1308 二、二因素随机区组试验分析实例 SAS另例