章 第八章复因子试验方差分析 课时 4 &8.1复因子试验概述 &8.2二因素随机区组设计的结果分析 &8.3三因素随机区组设计的结果分析&8.4二因素裂区设计的结果分析 &8.5正交试验统计分析 教学 通过讲授,使学生了解复因子试验的必要性和优越性,掌握完全随机设计、 目的 随机区组设计、正交设计试验的方差分析,了解裂区试验资料的分析方法, 教学 重点 重点两因子(完全随机设计、随机区组设计和正交设计)试验的分析方法 教学 裂区试验的分析法、正交试验资料的分析。 难点 相关素材(参考资料、指导学生阅读材料等): 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008, 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9.《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10.《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002, 11.《试验设计与分析》,袁志发主编,高等教育出版社,2000
1 章 第八章 复因子试验方差分析 课时 4 节 &8.1 复因子试验概述 &8.2 二因素随机区组设计的结果分析 &8.3 三因素随机区组设计的结果分析 &8.4 二因素裂区设计的结果分析 &8.5 正交试验统计分析 教学 目的 通过讲授,使学生了解复因子试验的必要性和优越性,掌握完全随机设计、 随机区组设计、正交设计试验的方差分析,了解裂区试验资料的分析方法。 教学 重点 重点两因子(完全随机设计、随机区组设计和正交设计)试验的分析方法。 教学 难点 裂区试验的分析法、正交试验资料的分析。 相关素材(参考资料、指导学生阅读材料等): 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11. 《试验设计与分析》,袁志发主编,高等教育出版社,2000
教师授课思路、设问及讲解要点 “、引言 科研试验往往进行的是复因子试验,不仅要分析各因子水平间的比较、还分析 因子间的互作,处理组合效应的比较,即综合效果。本章将学习常用于复因子试验 设计资料的方差分析法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &8.1复因子试验概述 一、复因子试验的必要性 不仅能解决各因子水平间的比较问题,且能分析因子间的互作问题。 与同条件下的单因子试验精确度高 二、单、复因子试验方差分析不同点 1.必须将处理组合的SS和DF进一步分解为各个因子及其各项交互作用的SS 和D吓,从而进行因子主效应及交互作用效应的F测验。 2.要用二项表来计算各因子及各项交互作用的平方和 教 例如:2×4复因子试验,试作自由度分析。 (1)采用完全随机排列设计,重复3次 学 (2)采用随机区组设计,重复3次 (3)采用丁方设计 过 课堂练习: 2×3×4复因子试验,采用随机区组设计,重复3次,试作自由度分析。 &82二因子随机区组设计的结果分析 、 二因子随机区组试验的线性模型和期望均方 设有A、B两个试验因素,A因素有a个水平,B因素有b个水平,采用随机 区组设计,重复r次。共有b个水平组合,每一个水平组合有r个观察值。则该试 验共有rab个观察值。 变异来源DF SS MS 区组 r-1 MS. 处理组合 ab-1 SS, ΣT2-c MS A a-1 5S,= ∑i-c MSA b-1 s5=2-c MSB AXB (a-1b-1) SS4B =SS,-SS-SS8 MSA×B SS。=SS,-SS.-SS, 误差 (-lab-1) SS,=∑x2M-C MSe 总变异 rab-1
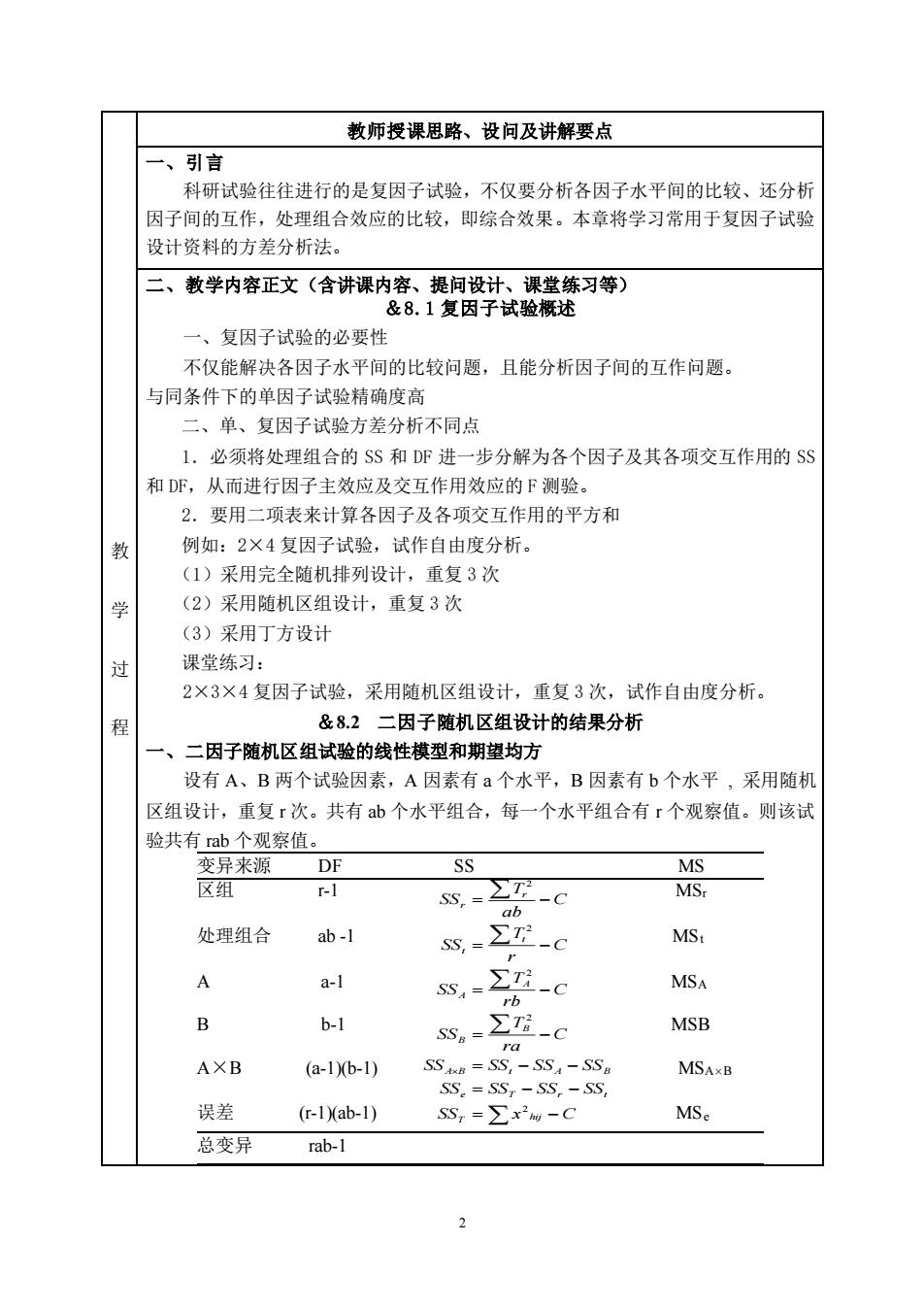
2 教 学 过 程 教师授课思路、设问及讲解要点 一、引言 科研试验往往进行的是复因子试验,不仅要分析各因子水平间的比较、还分析 因子间的互作,处理组合效应的比较,即综合效果。本章将学习常用于复因子试验 设计资料的方差分析法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &8.1 复因子试验概述 一、复因子试验的必要性 不仅能解决各因子水平间的比较问题,且能分析因子间的互作问题。 与同条件下的单因子试验精确度高 二、单、复因子试验方差分析不同点 1.必须将处理组合的 SS 和 DF 进一步分解为各个因子及其各项交互作用的 SS 和 DF,从而进行因子主效应及交互作用效应的 F 测验。 2.要用二项表来计算各因子及各项交互作用的平方和 例如:2×4 复因子试验,试作自由度分析。 (1)采用完全随机排列设计,重复 3 次 (2)采用随机区组设计,重复 3 次 (3)采用丁方设计 课堂练习: 2×3×4 复因子试验,采用随机区组设计,重复 3 次,试作自由度分析。 &8.2 二因子随机区组设计的结果分析 一、二因子随机区组试验的线性模型和期望均方 设有 A、B 两个试验因素,A 因素有 a 个水平,B 因素有 b 个水平 , 采用随机 区组设计,重复 r 次。共有 ab 个水平组合,每一个水平组合有 r 个观察值。则该试 验共有 rab 个观察值。 变异来源 DF SS MS 区组 r-1 MSr 处理组合 ab -1 MSt A a-1 MSA B b-1 MSB A×B (a-1)(b-1) MSA×B 误差 (r-1)(ab-1) MSe 总变异 rab-1 SS x C SS SS SS SS SS SS SS SS C raT SS C rbT SS C rT SS C abT SS hij T e T r t A B t A B B B A A t t r r = − = − − = − − = − = − = − = − 2 2 2 2 2
二因素随机区组的期望均方 变异 期望均方 来源 固定模型 随机模型 区组 o 2e+rb x2A B o 2+rak 2B a 2e+r o 2(AxB)+ra o 2B AXB a2e+rK 2(AxB) 02+r02A×B 误差 02。 02。 对于多因素试验而言,效应模型的不同将导致F测验的方法不同。 对固定模型来说,各变异项的均方除误差均方即构成相应的F测验。 H。:x2=0H。:x=0H。:x6=0,H。:x2B=0 MS技项 MS 但对随机模型来说,区组变异和互作变异用误差均方进行F测验:而A、B的 变异则应用互作项的均方进行F测验。 二因素随机区组与单因素随机区组的差别:二因素试验的处理项可以再分解为 教 A因素水平间、B因素水平间和AB互作三部分: SSt SSA+SSB+SSAxB (ab-1(a-1+b-1(a-1b-1) 其中,SS:为处理平方和:SSAxB为互作项平方和;SSA为A因素平方和;SSE 过 为B因素平方和。 二、二因素随机区组试验结果的分析实例 程 [例9.1]橡胶树品系A与栽培密度B试验,采用随机区组设计重复4次,测得 小区年干胶产量如下表,试作方差分析。 处理组合 A2 区组和 区组 B2 B3 BI B3 区组1 56 60 66 65 60 53 360 区组2 45 50 57 61 58 324 区组3 3 45 50 60 56 302 区组4 46 48 50 63 60 55 322 处理总和 190203223249 234209 T=1308 解 第一步:资料整理计算娇正数及各种平方和 Cs 13082 bn2x3x4=7186
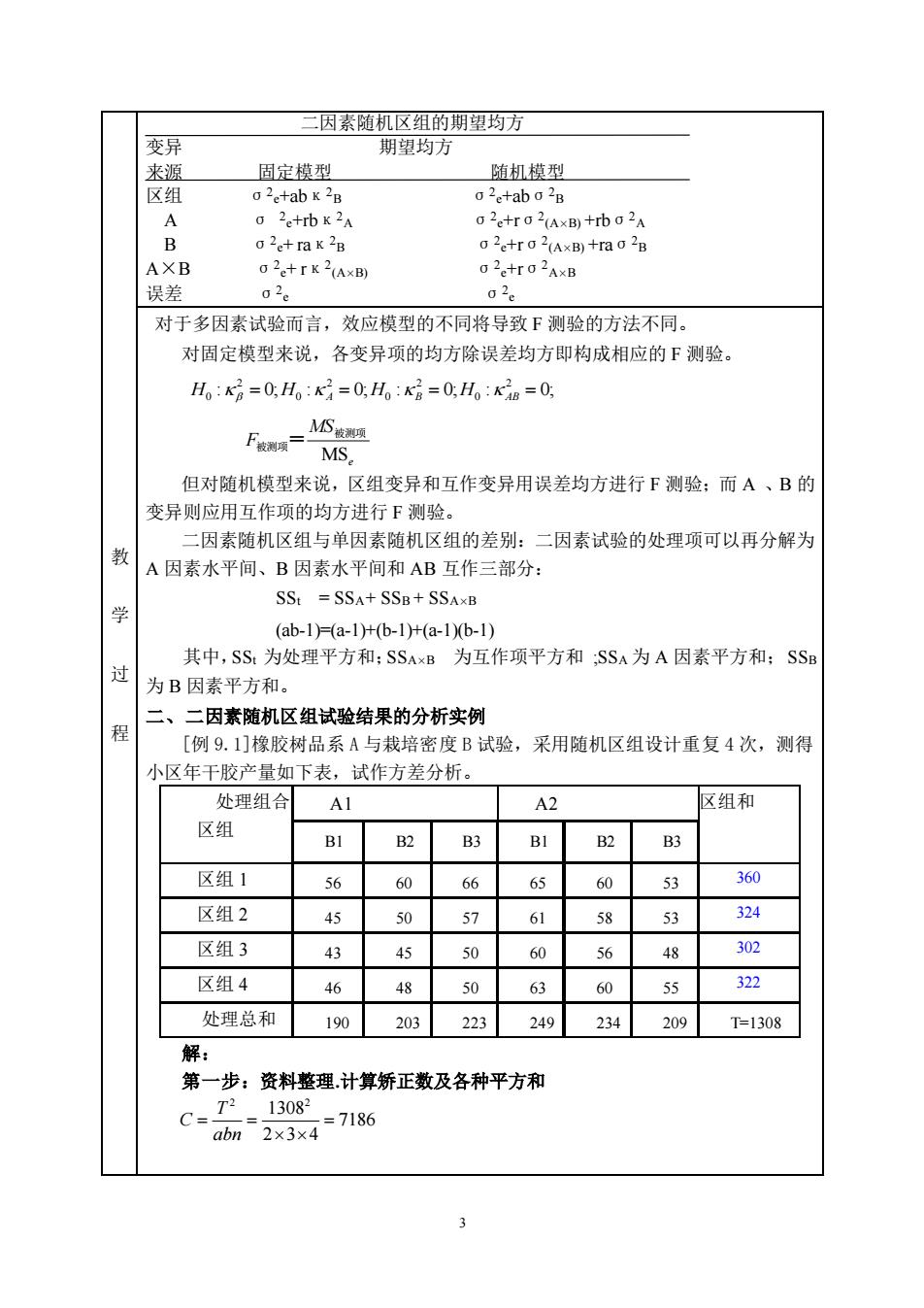
3 教 学 过 程 二因素随机区组的期望均方 变异 期望均方 来源 固定模型 随机模型 区组 σ2 e+abκ2 B σ2 e+abσ2 B A σ 2 e+rbκ2 A σ2 e+rσ2 (A×B) +rbσ2 A B σ2 e+ raκ2 B σ2 e+rσ2 (A×B) +raσ2 B A×B σ2 e+ rκ2 (A×B) σ2 e+rσ2 A×B 误差 σ2 e σ2 e 对于多因素试验而言,效应模型的不同将导致 F 测验的方法不同。 对固定模型来说,各变异项的均方除误差均方即构成相应的 F 测验。 e MS F MS 被测项 被测项 = 但对随机模型来说,区组变异和互作变异用误差均方进行 F 测验;而 A 、B 的 变异则应用互作项的均方进行 F 测验。 二因素随机区组与单因素随机区组的差别:二因素试验的处理项可以再分解为 A 因素水平间、B 因素水平间和 AB 互作三部分: SSt = SSA + SSB + SSA×B (ab-1)=(a-1)+(b-1)+(a-1)(b-1) 其中,SSt 为处理平方和;SSA×B 为互作项平方和 ;SSA 为 A 因素平方和;SSB 为 B 因素平方和。 二、二因素随机区组试验结果的分析实例 [例 9.1]橡胶树品系 A 与栽培密度 B 试验,采用随机区组设计重复 4 次,测得 小区年干胶产量如下表,试作方差分析。 处理组合 区组 A1 A2 区组和 B1 B2 B3 B1 B2 B3 区组 1 56 60 66 65 60 53 360 区组 2 45 50 57 61 58 53 324 区组 3 43 45 50 60 56 48 302 区组 4 46 48 50 63 60 55 322 处理总和 190 203 223 249 234 209 T=1308 解: 第一步:资料整理.计算矫正数及各种平方和 7186 2 3 4 1308 2 2 = = = abn T C : 0; : 0; : 0; : 0; 2 0 2 0 2 0 2 H0 = H A = H B = H AB =
SS。=∑Σx2-C=562+602++552-C=1036 5=7g-C=360+324++32-C=2913 2×3 %=27-C-190+203+ .+2092 -c=583 SS =SSg-SSs-SS=161.67 为了进一步分析处理间引起的变异原因,列出二向表, 以方便计算因子交互作用平方和。 BBI B2 B3 A和 A 190203 223 616 A2249234 209692 B和439437 4321308 学 ,=7 -c=6162+692 bn 3×4 -c=240.67 过 -c=439+4372+432 -c=325 an 2×4 55B=SS处n一S3A-5SB=339.08 第二步:列方差分析表并进行下测验 变异来源 自由度 平方和 均方 F值 区组 3 291.33 97.11 9.01 处理组合 583.00 116.60 10.82 品系A 240.67 240.67 22.33 施肥B 2 3.25 1.63 <1 交互AB 2 339.08 169.54 15.73 机误 161.67 10.78 总变异 1036.00 F测验结论: 7 第三步:多重比较(Duncan测验)(a=5%) 1.A多因子水平间(不用)
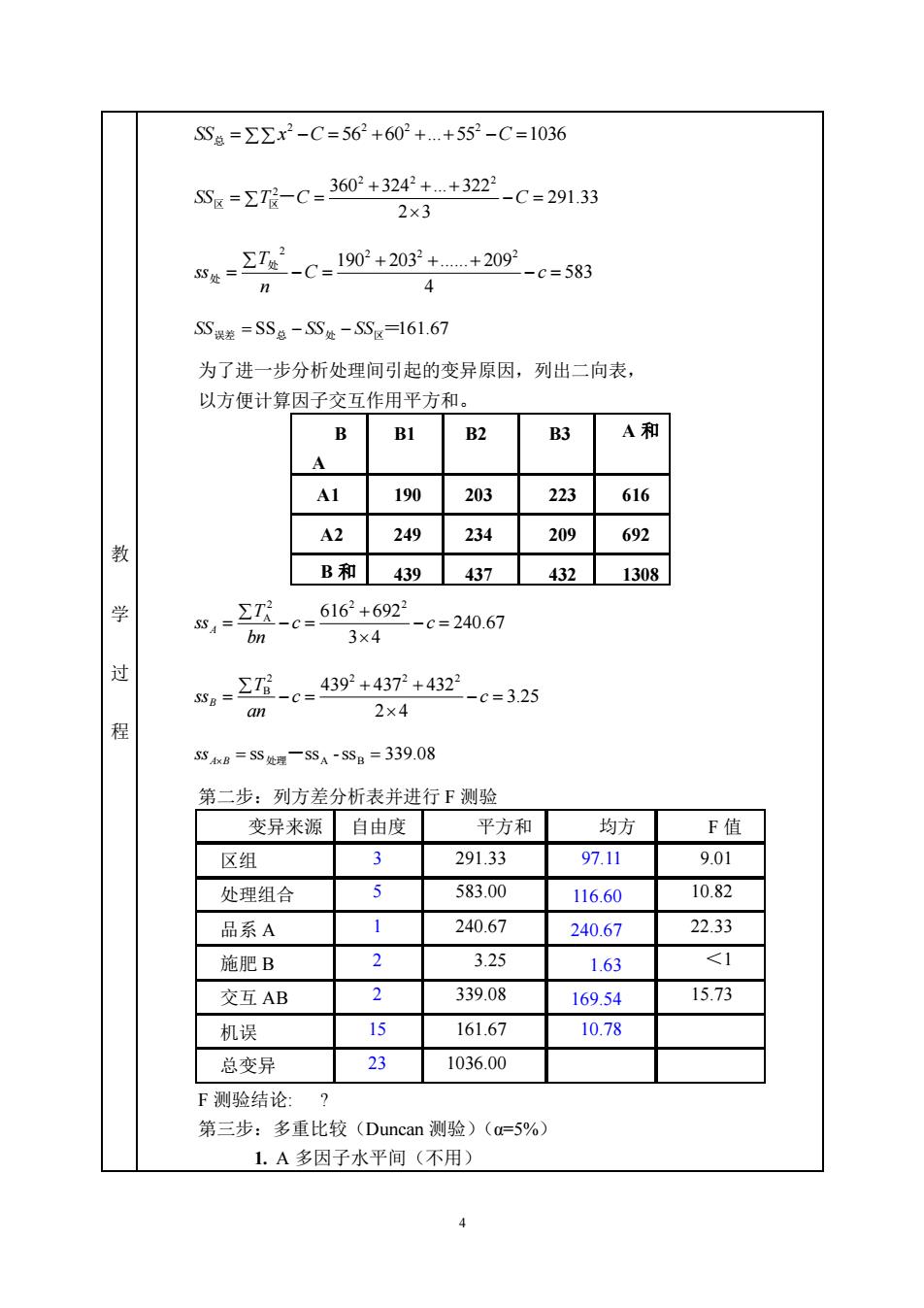
4 教 学 过 程 = − = 56 +60 +.+55 − =1036 2 2 2 2 SS总 x C C 291.33 2 3 360 324 . 322 2 2 2 2 − = + + + SS区 = T区-C = C 583 4 190 203 . 209 2 2 2 2 − = + + + − = = C c n T ss 处 处 SS误差 = SS总 − SS处 − SS区 =161.67 为了进一步分析处理间引起的变异原因,列出二向表, 以方便计算因子交互作用平方和。 B A B1 B2 B3 A 和 A1 190 203 223 616 A2 249 234 209 692 B 和 439 437 432 1308 240.67 3 4 616 692 2 2 2 A − = + − = = c c bn T ssA 3.25 2 4 439 437 432 2 2 2 2 B − = + + − = = c c an T ssB ssAB = ss处理-ssA -ssB = 339.08 第二步:列方差分析表并进行 F 测验 变异来源 自由度 平方和 均方 F 值 区组 3 291.33 97.11 9.01 处理组合 5 583.00 116.60 10.82 品系 A 1 240.67 240.67 22.33 施肥 B 2 3.25 1.63 <1 交互 AB 2 339.08 169.54 15.73 机误 15 161.67 10.78 总变异 23 1036.00 F 测验结论: ? 第三步:多重比较(Duncan 测验)(α=5%) 1. A 多因子水平间(不用)
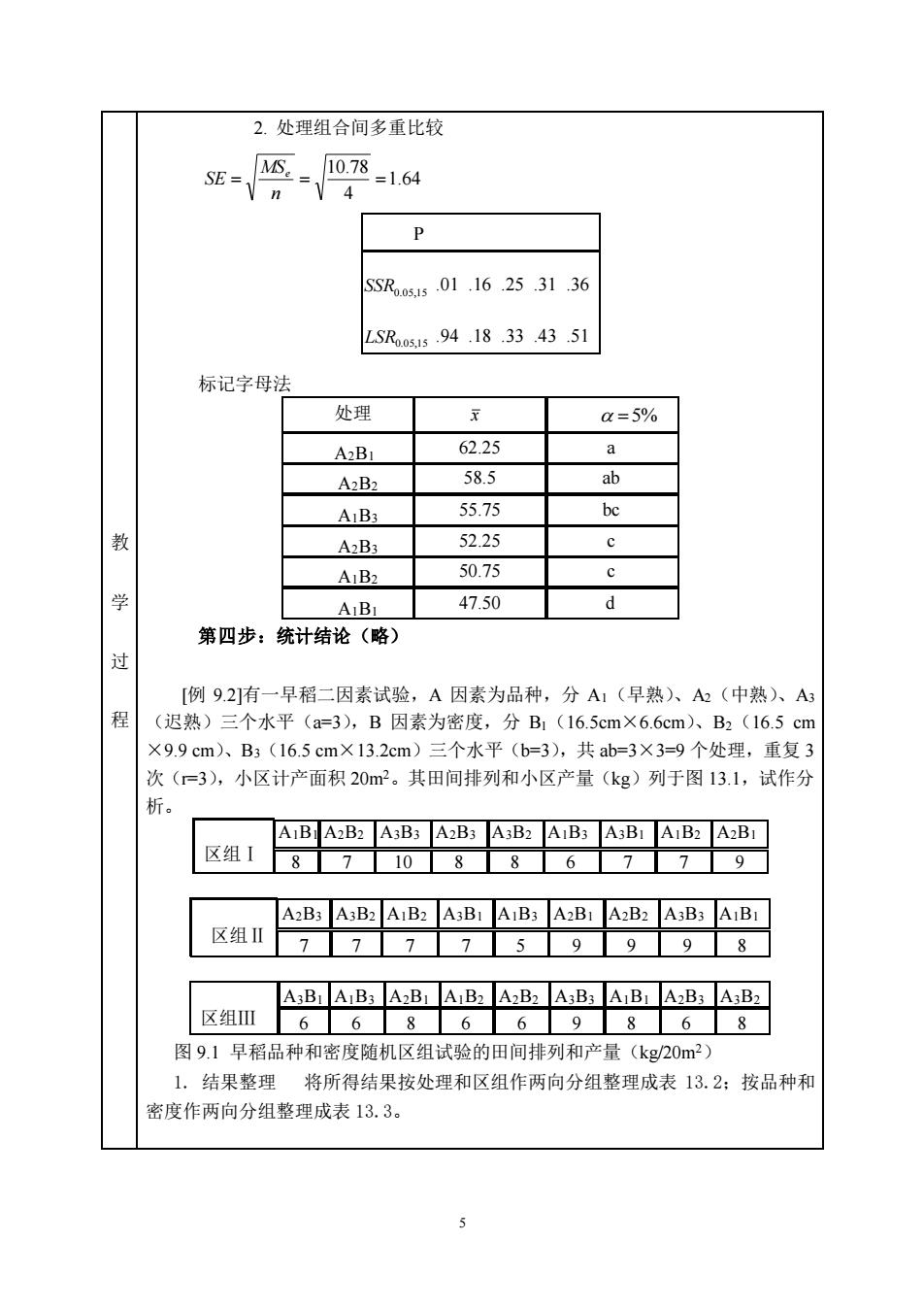
2.处理组合间多重比较 s.078-1.64 SE-V4 p SSRs501.16253136 LSR5594.18.3343.51 标记字母法 处理 a=5% A2BI 62.25 a A2B2 58.5 ab AB3 55.75 bc 教 A2B3 52.25 c AB2 50.75 c AiBI 47.50 d 第四步:统计结论(略) 过 [例9.2]有一早稻二因素试验,A因素为品种,分A1(早熟)入、A(中熟)、A3 程(迟熟)三个水平(a=3),B因素为密度,分B1(16.5cm×6.6cm)、B2(16.5cm ×9.9cm)、B;(16.5cm×13.2cm)三个水平(b=3),共ab=3×3=9个处理,重复3 次(=3),小区计产面积20m2。其田间排列和小区产量(kg)列于图13.1,试作分 析 AiBA2B2 A3B3 A2B3 A3B2 AiB3 A3BIAiB2 A2BI 区组18710886779 A2B3 A3B2A1B2 A3B1AIB3 A2BI A2B2 A3B3 A1BI 区组"777759998□ A3B:AiB:A2B:A:B2 A2B2 A:B:AuB:A2B:A:B2 区细m663669868 图9.1早稻品种和密度随机区组试验的田间排列和产量(kg20m2) 1.结果整理将所得结果按处理和区组作两向分组整理成表13.2:按品种和 密度作两向分组整理成表13.3
5 教 学 过 程 2. 处理组合间多重比较 1.64 4 10.78 = = = n MS SE e P 2 3 4 5 6 SSR0.05,15 3 .01 3 .16 3 .25 3 .31 3 .36 LSR0.05,15 4 .94 5 .18 5 .33 5 .43 5 .51 标记字母法 处理 x = 5% A2B1 62.25 a A2B2 58.5 ab A1B3 55.75 bc A2B3 52.25 c A1B2 50.75 c A1B1 47.50 d 第四步:统计结论(略) [例 9.2]有一早稻二因素试验,A 因素为品种,分 A1(早熟)、A2(中熟)、A3 (迟熟)三个水平(a=3),B 因素为密度,分 B1(16.5cm×6.6cm)、B2(16.5 cm ×9.9 cm)、B3(16.5 cm×13.2cm)三个水平(b=3),共 ab=3×3=9 个处理,重复 3 次(r=3),小区计产面积 20m2。其田间排列和小区产量(kg)列于图 13.1,试作分 析。 区组Ⅰ A1B1 A2B2 A3B3 A2B3 A3B2 A1B3 A3B1 A1B2 A2B1 8 7 10 8 8 6 7 7 9 区组Ⅱ A2B3 A3B2 A1B2 A3B1 A1B3 A2B1 A2B2 A3B3 A1B1 7 7 7 7 5 9 9 9 8 区组Ⅲ A3B1 A1B3 A2B1 A1B2 A2B2 A3B3 A1B1 A2B3 A3B2 6 6 8 6 6 9 8 6 8 图 9.1 早稻品种和密度随机区组试验的田间排列和产量(kg/20m2) 1. 结果整理 将所得结果按处理和区组作两向分组整理成表 13.2;按品种和 密度作两向分组整理成表 13.3

表13.2图13.1资料区组和处理产量的两向表 处理区组区组Ⅱ区组m总和。 AB. 8 AB. 10 9 总和70 68 63 1=201 表13.3表13.2资料品种()和密度(B)的两向表 教 20 28 70 65 66201 2.自由度和平方和的分解自由度的分解可按表13.1直接填入表13.4。以下分解各变异来源的 学 平方和。 2012 63×8x3=14963 由表13.2按单因素随机区组的分析方法可得: 程 5S,=2y4-C=82+82++92-C=40.67 ,-72-C702+68+63 -C=2.89 ab 3×3 8,-27-c.24+202++282-c-30.00 3 SS.=5Sr5S-SS=40.67-30.00-2.89=7.78 由表13.3对SS=29.67进行再分解: -C-612+692+71e -C=6.23 rb 3×3 5,-31-c-702+652+6-c=1.56 a 3×3 55F5555r55F30.00-6.23-1.56=22.21 3.方差分析表和F测验将上述结果列于表13.4。这里对A和B两因素皆 取固定模型,区组则取随机模型,因此各项变异来源的5均可用对误差项S的比 进行F测验。取显著水平a=0.05。表13.4的F测验说明:区组间、密度间差异不 显著,而品种间与品种×密度间的差异都显著。由此说明,不同品种有不同 6
6 教 学 过 程 表 13.2 图 13.1 资料区组和处理产量的两向表 处 理 区组Ⅰ 区组Ⅱ 区组Ⅲ 总和 TAB A1B1 8 8 8 24 A1B2 7 7 6 20 A1B3 6 5 6 17 A2B1 9 9 8 26 A2B2 7 9 6 22 A2B3 8 7 6 21 A3B1 7 7 6 20 A3B2 8 7 8 23 A3B3 10 9 9 28 总和 Tr 70 68 63 T=201 表 13.3 表 13.2 资料品种(A)和密度(B)的两向表 B1 B2 B3 TA A1 24 20 17 61 A2 26 22 21 69 A3 20 23 28 71 TB 70 65 66 T=201 2. 自由度和平方和的分解 自由度的分解可按表 13.1 直接填入表 13.4。以下分解各变异来源的 平方和。 1496.33 3 3 3 2012 = = = rab T C 2 由表 13.2 按单因素随机区组的分析方法可得: 8 8 9 40.67 2 2 2 SS = y − C = + + + − C = abr T jkl 1 2 C ab T SS r R − = 2 − = + + = C 3 3 70 68 63 2 2 2 2.89 C r T SS AB t − = 2 = −C + + + 3 24 20 28 2 2 2 =30.00 SSe=SST-SSt-SSR=40.67-30.00-2.89=7.78 由表 13.3 对 SSt=29.67 进行再分解: C rb T SS A A − = 2 = 6.23 3 3 61 69 71 2 2 2 − = + + C C ra T SS B B − = 2 = 1.56 3 3 70 65 66 2 2 2 − = + + C SSAB=SSt-SSA-SSB=30.00-6.23-1.56=22.21 3. 方差分析表和 F 测验 将上述结果列于表 13.4。这里对 A 和 B 两因素皆 取固定模型,区组则取随机模型,因此各项变异来源的 MS 均可用对误差项 MS 的比 进行 F 测验。取显著水平 =0.05。表 13.4 的 F 测验说明:区组间、密度间差异不 显著,而品种间与品种×密度间的差异都显著。由此说明,不同品种有不同

的生产力,而不同品种又要求有相应不同的密度。所以需进一步测验品种间与品种 ×密度间的差异显著性。 表13.4水稻品种与密度二因素试验的方差分析 变异来源 F S Fios 区组间 2 2.89 1.45 2.96 363 处理(组合)间 8 30.00 375 29 256 078 L59 363 品种X密度 422.21 5.5 11.33 3.01 误 167.78 0.49 总容异 2640.67 4.差异显著性测验 (1)品种间比较此处以各品种的小区平均数(将表13.3的各个T:值除以b-9)进行新复 极差测验。假设为h:,=%=h对:严%、不全相等。算符 0.49-0.233kg - 查附表7,=2时,5Ss.6=3.00,5SKu6=4.13:=3时,5SRs6=3.15,SS况o 6=4.34,因此据L5SR。=SE×SSR。,得=2时,LSB6.6=3.00×0.233=0.70(kg) 学 LSR1.6=4.13×0.233=0.96(kg);pF3时,LSR.s.16=3.15×0.233=0.73,LSR.m 6=4.34×0.233=1.01(kg)。其测验结果列于表13.5。表13.5说明:A和A无显著 过 差异,但A和A的差异达a=0.01水平,A和A的差异达a=0.05水平。因此,就 品种的平均效应而言,A和A都是比较好的,但A的生育期比A短,对安排后作有 程 利。故与季节矛盾不突出时,选用Aa、Aa皆可,否则宜选用Aa。 表13.5三个品种小区平均产量的新复极差测验 品种产量 差异显著性 5% 1% 7.9 a 6.8 (2)品种×密度的互作 由于品种×密度的互作是极显著的,说明各品种所要求的最适密度 可能不相同。因此,可分别计算各品种不同密度的简单效应,以分析互作的具体情形。将表13.2 各个T4除以=3,即得各品种在不同密度下的小区平均产量(kg20m于表13.6。 A品科 4品种 品种产量差异显著性 5% 1% 品种产量差异显著性 5%1% 品种产量若异显著性 51% B 8.0 B.8.7 a A B9.3a A 6.7 b AB B. 7.3 b AB B7.7 b AB 5.7 B. 7.0 h B6.7 h 7
7 教 学 过 程 的生产力,而不同品种又要求有相应不同的密度。所以需进一步测验品种间与品种 ×密度间的差异显著性。 表 13.4 水稻品种与密度二因素试验的方差分析 变 异 来 源 DF SS MS F F0.05 区 组 间 2 2.89 1.45 2.96 3.63 处理(组合)间 8 30.00 3.75 7.65* 2.59 品 种 26.23 3.12 6.37* 3.63 密 度 21.56 0.78 1.59 3.63 品种×密度 422.21 5.55 11.33* 3.01 误 差 16 7.78 0.49 总 变 异 26 40.67 4. 差异显著性测验 (1) 品种间比较 此处以各品种的小区平均数(将表 13.3 的各个 TA 值除以 rb=9)进行新复 极差测验。假设为 H0: = A1 = A2 A3 对 HA: A1 、 A2 、 A3 不全相等。算得 9 0.49 = = rb MS SE e =0.233(kg) 查附表 7,p=2 时,SSR0.05,16=3.00,SSR0.01,16=4.13;p=3 时,SSR0.05,16=3.15,SSR0.01, 16 =4.34,因此据 LSR = SE × SSR ,得 p=2 时,LSR0.05,16=3.00×0.233=0.70(kg), LSR0.01,16=4.13×0.233=0.96(kg);p=3 时,LSR0.05,16=3.15×0.233=0.73,LSR0.01, 16=4.34×0.233=1.01(kg)。其测验结果列于表 13.5。表 13.5 说明:A3和 A2无显著 差异,但 A3和 A1的差异达 =0.01 水平,A2和 A1的差异达 =0.05 水平。因此,就 品种的平均效应而言,A3和 A2都是比较好的,但 A2的生育期比 A3短,对安排后作有 利。故与季节矛盾不突出时,选用 A3、A2皆可,否则宜选用 A2。 表 13.5 三个品种小区平均产量的新复极差测验 品 种 产 量 差异显著性 5% 1% A3 7.9 a A A2 7.7 a AB A1 6.8 b B (2) 品种×密度的互作 由于品种×密度的互作是极显著的,说明各品种所要求的最适密度 可能不相同。因此,可分别计算各品种不同密度的简单效应,以分析互作的具体情形。将表 13.2 各个 TAB 除以 r=3,即得各品种在不同密度下的小区平均产量(kg/20m 2 )于表 13.6。 表 13.6 各品种在不同密度下的小区平均平均产量及其差异显著性 A1品种 A2 品种 A3品种 品 种 产 量 差异显著性 品 种 产 量 差异显著性 品 种 产 量 差异显著性 5% 1% 5% 1% 5% 1% B1 8.0 a A B1 8.7 a A B3 9.3 a A B2 6.7 b AB B2 7.3 b AB B2 7.7 b AB B3 5.7 b B B3 7.0 b B B1 6.7 b B

对表13.6各个差数新复极差测验,有A,品种:H,=“a:=4,品种h: “a=“,=4a,和A品种:“=“,=“a,算得SE=S,下=493-0.404kg】 并有:=2时,LSRs.6=1.21,LS泥,6=1.67(kg),=3时,LS%s.6=1.27,LS况o 6=1.75(kg)。用此尺度测验表13.6的各个差数,结果A、A品种都以B,为优,并 与B、B有显著差异:而A品种则以B为优,并与B、B有显著差异。这种不同情 况就是品种和密度存在互作的反应。所以A品种应选B密度,而A、A品种则应选 B密度。 要比较全部9个处理组合间差异的显著性,可以将表13.6中(1)、(2)、(3)合 成一张表,然后计算F2至9的LSR值,这里从略。 以上是间接地测验互作。对互作值也可进行直接测验。例如,若要测定二个产 量较高品种A和A与密度的互作,则可将这两个品种在3种密度下各3个小区的总 产量(kg)列成表13.7。然后,计算各密度下A-A的差数。如果A和B没有互作, 则A的简单效应不因B的不同水平而异,这些差数应无显著差异。所以差数的差数 即为互作值。由表13.7可算得:6-(-1)=7,表示A比A的增产数在B,水平下比B 教 水平下多7kg:同理6-(-7)=13,表示比A增产数在B水平下比B水平下多13kg -1-(-7)=6表示A比A增产数在B水平下比B,水平下多6kg。这些互作值的计算世 学 可写成以下形式: (4,B+4B)-(4R+4B)=23+26-20-22=7(kg) (4B+4B)-(4B+4A)=28+26-20-21=13(kg) (AB+AB)-(AB+AB)=28+22-23-21=6(kg) 程 表13.7品种密度互作值的计算 AA差数(A-A)互作值(差数的差数) 26 20 6 2223 -1 7 B.2128 -7 13 6 由此,以上的各个互作值是6个小区总和为基础的差数,故在测验互作的显老 性时SE=VnS.=6x0.49=1.7kg.此处F2b,并有:F2时,LS况s5.,LS8。 16=7.0(kg),=3时,LS泥s.6=5.4,LSR,6=7.4(kg)。因而上述互作值都达到了 a=0.05或a=0.01的显著水平。故A品种需采用B,才能充分利用其互作,取得 最好产量。 5.试验结论本试验品种主效有显著差异,以A产量最高,与A有显著差 异,而与A无显著差异。密度主效无显著差异。但品种和密度的互作极显著,A品 种需用B密度,A2品种需用B密度,才能取得最高产量
8 教 学 过 程 对表 13.6 各个差数新复极差测验,有 A1品种 H0: = B1 = B 2 B3 ,A2品种 H0: = B1 = B 2 B3 和 A3品种 H0: = B1 = B 2 B3 算得 SE = MSe r = 0.49/3 =0.404(kg), 并有:p=2 时,LSR0.05,16=1.21,LSR0.01,16=1.67(kg),p=3 时,LSR0.05,16=1.27,LSR0.01, 16 =1.75(kg)。用此尺度测验表 13.6 的各个差数,结果 A1、A2品种都以 B1为优,并 与 B2、B3有显著差异;而 A3品种则以 B3为优,并与 B2、B1有显著差异。这种不同情 况就是品种和密度存在互作的反应。所以 A3品种应选 B3密度,而 A2、A1品种则应选 B1密度。 要比较全部 9 个处理组合间差异的显著性,可以将表 13.6 中(1)、(2)、(3)合 成一张表,然后计算 p=2 至 9 的 LSR 值,这里从略。 以上是间接地测验互作。对互作值也可进行直接测验。例如,若要测定二个产 量较高品种 A3和 A2与密度的互作,则可将这两个品种在 3 种密度下各 3 个小区的总 产量(kg)列成表 13.7。然后,计算各密度下 A2-A3的差数。如果 A 和 B 没有互作, 则 A 的简单效应不因 B 的不同水平而异,这些差数应无显著差异。所以差数的差数 即为互作值。由表 13.7 可算得:6-(-1)=7,表示 A2比 A3的增产数在 B1水平下比 B2 水平下多 7kg;同理 6-(-7)=13,表示 A2比 A3增产数在 B1水平下比 B3水平下多 13kg; -1-(-7)=6 表示 A2比 A3增产数在 B2水平下比 B3水平下多 6kg。这些互作值的计算也 可写成以下形式: (A3B2+A2B1)-(A3B1+A2B2)=23+26-20-22=7(kg) (A3B3+A2B1)-(A3B1+A2B3)=28+26-20-21=13(kg) (A3B3+A2B2)-(A3B2+A2B3)=28+22-23-21=6(kg) 表 13.7 品种密度互作值的计算 A2 A3 差数(A2-A3) 互作值(差数的差数) B1 26 20 6 B2 22 23 -1 7 B3 21 28 -7 13 6 由此,以上的各个互作值是 6 个小区总和为基础的差数,故在测验互作的显著 性时 SE = nMSe = 6 0.49 =1.7(kg)。此处 n=2b,并有:p=2 时,LSR0.05,16=5.1,LSR0.01, 16=7.0(kg),p=3 时,LSR0.05,16=5.4,LSR0.01,16=7.4(kg)。因而上述互作值都达到了 = 0.05 或 = 0.01 的显著水平。故 A3品种需采用 B3,才能充分利用其互作,取得 最好产量。 5. 试验结论 本试验品种主效有显著差异,以 A3产量最高,与 A1有显著差 异,而与 A2无显著差异。密度主效无显著差异。但品种和密度的互作极显著,A3品 种需用 B3密度,A2品种需用 B1密度,才能取得最高产量

&8.3三因素随机区组设计的结果分析 1.三因素随机区组试验的线性模型与期望均方 设试验有A,B,C三个因素,各具有a,b,c个水平,且将abc个处理安排名 r个随机完全区组内,则该试验有rabc个观察值。由于有A,B,C三个因素参加试 验,处理效应则为三个因素的总效应,它可以分解为A,B,C,(AB,(AC), (BC).和(ABC)七个部分。 各观察值的线性模型为: mm=+B+A+B+(AB)y+(AC)+(BC)n+(ABC)ok+ekub 式中:h=1,2,.,r: ie1,2,.,a: jl,2,.,b k=1,2,.,c 1、三因素随机区组试验结果的分析示例 p253[例13.2]水稻品种、赤霉素处理、光照处理的三因素完全随机试验数据的 分析。试验中有3个品种(A因素),2个水平的激素处理[喷水处理(对照)和设 学 施20mg/L的赤霉素],2个水平的光照处理(增加光照C,和自然光C2),共计3× ×2=12个处理组合。将水稻种子采用盆播,完全随机排列,除此三因素外,其它环 过 境条件基本一致。试验的目的是考察三个因素及其交互作用对于苗高的影响。将试 验结果列于表13.9。 程 表13.9品种、激素处理、光照三因素的水稻苗高试验结果 A因素B因素 C因素 观察值(cm) TABC C,(加光 16.319.6 20.418.3 19.6 94.2 17.6173187 19.1 882 A B2 C1(加光)30.9 35.6 332 32.6 36.6 168.9 (20mgL)C2(自然光)284 23.9 26.0 24.0 292 131.5 C(加光) 187 184 15.1 17.9 174 87.5 (0mgL)C2(自然光)15.6 156 17.8 17.7 16.7 83.4 A2 B2 C(加光) 282 34.3 32.1 26.2 29.0 149.8 (20mgL)C2(自然光)27.7 27.2 22.3 18.0 20.3 115.5 C(加光) 18.9 17.7 18.0 15.9 15.6 86.1 A3 (0mgL)C2(自然光) 16.1 10.8 14.7 15.2 12.6 69.4 C1(加光) 40.8 38.7 35.1 41.0 42.9 198.5 (20mgL)C2(自然光)27.231.327.129.1250139.7 其理论上的计算自学p253-255 9
9 教 学 过 程 &8.3 三因素随机区组设计的结果分析 1.三因素随机区组试验的线性模型与期望均方 设试验有 A,B,C 三个因素,各具有 a,b,c 个水平,且将 abc 个处理安排在 r 个随机完全区组内,则该试验有 rabc 个观察值。由于有 A,B,C 三个因素参加试 验,处理效应则为三个因素的总效应,它可以分解为 Ai,Bj,Ck,(AB)i j,(AC)ik, (BC)jk和(ABC)ijk 七个部分。 各观察值的线性模型为: hijk h i j i j i k j k ijk hijk x = x + + A + B + (AB) + (AC) + (BC) + (ABC) + e 式中:h=1,2,.,r; i=1,2,.,a; j=1,2,.,b; k=1, 2,.,c。 1、三因素随机区组试验结果的分析示例 p253[例 13.2]水稻品种、赤霉素处理、光照处理的三因素完全随机试验数据的 分析。试验中有 3 个品种(A 因素),2 个水平的激素处理[喷水处理(对照)和设 施 20mg/L 的赤霉素],2 个水平的光照处理(增加光照 C1和自然光 C2),共计 3×2 ×2=12 个处理组合。将水稻种子采用盆播,完全随机排列,除此三因素外,其它环 境条件基本一致。试验的目的是考察三个因素及其交互作用对于苗高的影响。将试 验结果列于表 13.9。 表 13.9 品种、激素处理、光照三因素的水稻苗高试验结果 A 因素 B 因素 C 因素 观察值(cm) TABC A1 B1 (0mg/L) C1(加光) 16.3 19.6 20.4 18.3 19.6 94.2 C2(自然光) 15.5 17.6 17.3 18.7 19.1 88.2 B2 (20mg/L) C1(加光) 30.9 35.6 33.2 32.6 36.6 168.9 C2(自然光) 28.4 23.9 26.0 24.0 29.2 131.5 A2 B1 (0mg/L) C1(加光) 18.7 18.4 15.1 17.9 17.4 87.5 C2(自然光) 15.6 15.6 17.8 17.7 16.7 83.4 B2 (20mg/L) C1(加光) 28.2 34.3 32.1 26.2 29.0 149.8 C2(自然光) 27.7 27.2 22.3 18.0 20.3 115.5 A3 B1 (0mg/L) C1(加光) 18.9 17.7 18.0 15.9 15.6 86.1 C2(自然光) 16.1 10.8 14.7 15.2 12.6 69.4 B2 (20mg/L) C1(加光) 40.8 38.7 35.1 41.0 42.9 198.5 C2(自然光) 27.2 31.3 27.1 29.1 25.0 139.7 其理论上的计算自学 p253-255

现看其SAS程序及输出 do B=1 to2 doC=1TO 2 don=l to 5 inputx@@; output; end: end;end:end; cards, 16.3 19.6 20.4 18.3 19.6., 25.0 proc anova class A B CN; model x=ABlc;means ABlc/duncan; means ABlc/duncan alpha=0.01; run; 教 SAS输出结果在上课SAS运行演示解释。 学 过 程
10 教 学 过 程 现看其 SAS 程序及输出 data aa; do A=1 to 3; do B=1 to 2; do C=1 TO 2; do n=1 to 5; input x@@; output; end; end; end; end; cards; 16.3 19.6 20.4 18.3 19.6 . . . . . . . . . . . . . 25.0 ; proc anova; class A B C N; model x=A|B|c;means A|B|c/duncan; means A|B|c/duncan alpha=0.01; run; SAS 输出结果在上课 SAS 运行演示解释