章 第六章卡平方测验 课时 2 &6.1卡平方测验概述 节 &6.2 适合性测验 &6.3独立性测验 教学 (①)了解卡平方的定义及其分布特点:(2)掌握次数资料的适合性测验和 目 独立性测验方法。 1.掌握次数资料的适合性测验法 教学 2.掌握次数资料的独立性测验,尤其2×2联列表x2测验 重点 1.x独立测验用基本公式时,各观测值相应理论值的计算。 教学 突破方法: 难点 举例说明,再总结出规律,总结求理论值的通式。主张用独立测验 的简化公式,举例说明公式中每个符号的含义,以便正确应用公式。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钧钻主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中因农业出版社,2007。 3. 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985 6 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10.《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11.《试验设计与分析》,袁志发主编,高等教有出版社,2000
1 章 第六章 卡平方测验 课时 2 节 &6.1 卡平方测验概述 &6.2 适合性测验 &6.3 独立性测验 教学 目的 (1)了解卡平方的定义及其分布特点;(2)掌握次数资料的适合性测验和 独立性测验方法。 教学 重点 1. 掌握次数资料的适合性测验法 2. 掌握次数资料的独立性测验,尤其 2×2 联列表 x 2 测验。 教学 难点 1. x 2 独立测验用基本公式时,各观测值相应理论值的计算。 突破方法: 举例说明,再总结出规律,总结求理论值的通式。主张用 x 2 独立测验 的简化公式,举例说明公式中每个符号的含义,以便正确应用公式。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11. 《试验设计与分析》,袁志发主编,高等教育出版社,2000
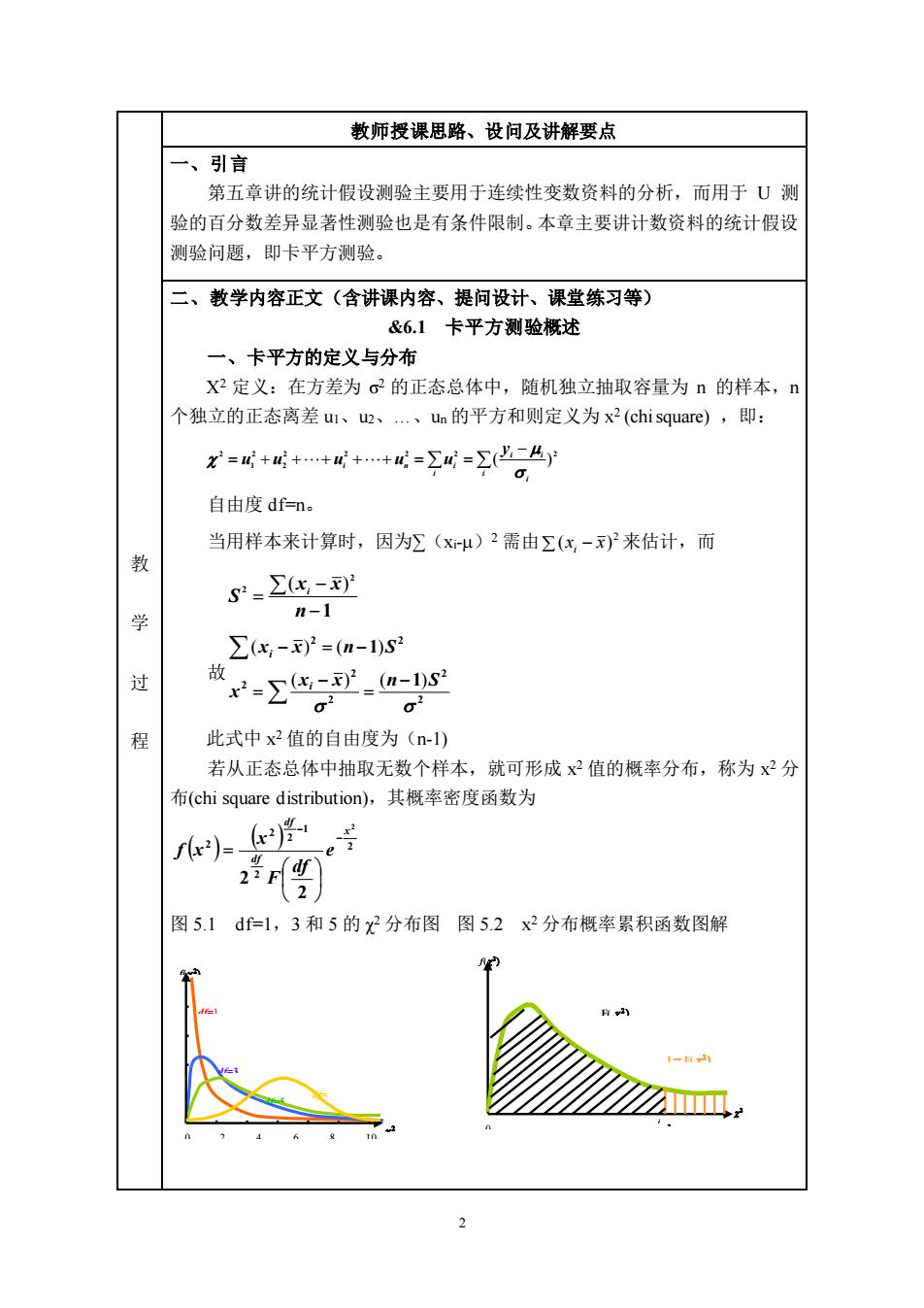
教师授课思路、设问及讲解要点 ,引言 第五章讲的统计假设测验主要用于连续性变数资料的分析,而用于U测 验的百分数差异显著性测验也是有条件限制。本章主要讲计数资料的统计假设 测验问题,即卡平方测验 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &6.1卡平方测验概述 一、卡平方的定义与分布 X2定义:在方差为c2的正态总体中,随机独立抽取容量为n的样本,n 个独立的正态离差uI、m的平方和则定义为x2(chisquare),即: 父=+G++度++成=2=y心二4 自由度dfm。 当用样本来计算时,因为∑(xμ)2需由Σ(化-)来估计,而 教 s=2s- n-1 ∑(x,-2=(m-1S2 过 -。.as 程 此式中x2值的自由度为(n-l) 若从正态总体中抽取无数个样本,就可形成x2值的概率分布,称为x2分 布(chi square distribution),其概率密度函数为 图5.1df=1,3和5的2分布图图52x2分布概率累积函数图解
2 教 学 过 程 教师授课思路、设问及讲解要点 一、引言 第五章讲的统计假设测验主要用于连续性变数资料的分析,而用于 U 测 验的百分数差异显著性测验也是有条件限制。本章主要讲计数资料的统计假设 测验问题,即卡平方测验。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &6.1 卡平方测验概述 一、卡平方的定义与分布 X2 定义:在方差为 σ 2 的正态总体中,随机独立抽取容量为 n 的样本,n 个独立的正态离差 u1、u2、.、un 的平方和则定义为 x 2 (chi square) ,即: 自由度 df=n。 当用样本来计算时,因为∑(xi-)2 需由 2 (x x) i − 来估计,而 故 2 2 2 2 2 2 2 1 1 x x n S x x x n S i i ( ) ( ) ( ) ( ) − = − = − = − 此式中 x 2 值的自由度为(n-1) 若从正态总体中抽取无数个样本,就可形成 x 2 值的概率分布,称为 x 2 分 布(chi square distribution),其概率密度函数为 ( ) ( ) 2 2 1 2 2 2 2 2 2 x df df e df F x f x − − = 图 5.1 df=1,3 和 5 的 χ 2 分布图 图 5.2 x 2 分布概率累积函数图解 − = + + + + + = = i i i i i i n i y u u u u u 2 2 2 2 2 2 2 1 2 ( ) 1 2 2 − − = n x x S i ( ) df=1 0 2 4 6 8 10 12 f( ) df=3 df=5 df= ∞ f( ) 0 F( ) 1-F( ) i

x2分布的特性有: ()x2分布的取值范围为0,+o0) (2x2分布的形状决定于自由度df。(图5.1)。 (3)x2分布曲线与横坐标轴所围成的面积等于1,即 p(0sx'(+)=[f(x'H(x')=1 x2分布的累积函数F(c2为F()=pk≤x》=f儿6) 二、x2测验公式 K.Pearson(1900)根据的x2上述定义从属性性状的分布推导出用于次数资 料(亦称计数资料)分析的x2公式: X心的基本公式:X=∑0-团 当d=1的样本,必须用连续性矫正公式:当d企2时,可以不作连续性矫 正。 火连续性桥正公式:心-Σ0-)-立 E 三、x2测验的应用 过 用于适合性测验:用于独立性测验:用于方差同质测验 四、x2测验的具体步骤 程 (1)提出无效假设与备择假设 (②)确定显著水平确定a=0.05或0.01等。 (3)计算x2值 由样本资料和理论假设计算 x2值:根据自由度,由附表4查出x2dF。 (4)推断,若X2≤2adf,则p>a,故接受Ho: Xadf,则p2时,可以不作连续性矫正
3 教 学 过 程 x 2 分布的特性有: ⑴ x 2 分布的取值范围为[0,+∞)。 ⑵x 2 分布的形状决定于自由度 df。(图 5.1)。 ⑶ x 2 分布曲线与横坐标轴所围成的面积等于 1,即 (0 ) ( ) ( ) 1 2 0 2 2 + = = + p x f x d x x 2 分布的累积函数 F( c2)为 ( ) ( ) ( ) ( ) 2 0 2 2 2 2 2 d x x F x p x f x i xi = = 二、x 2 测验公式 K.Pearson(1900)根据的 x 2 上述定义从属性性状的分布推导出用于次数资 料(亦称计数资料)分析的 x 2 公式: X2 的基本公式: − = i E O E 2 2 ( ) 当 df=1 的样本,必须用连续性矫正公式;当 df≥2 时,可以不作连续性矫 正。 X2 连续性矫正公式: − − = E O E xc 2 2 ] 2 1 [( ) 三、 x 2 测验的应用 用于适合性测验;用于独立性测验;用于方差同质测验 四、 x 2 测验的具体步骤 ⑴ 提出无效假设与备择假设 ⑵ 确定显著水平 确定 a=0.05 或 0.01 等。 ⑶ 计算 x 2 值 由样本资料和理论假设计算 x 2 值;根据自由度,由附表 4 查出 x 2 a,df 。 ⑷ 推断,若 χ 2≤χ2 a.df,则 p>α,故接受 H0; χ 2≥χ2 a.df ,则 p<α,故否定 H0; 卡平方测验均为一尾测验,且是右尾测验。 三、卡平方测验的连续性矫正 x 2 是连续分布,而次数资料是间断性的,由间断性资料计算的 x 2 值均有 不同程度偏大的趋势,尤其在 df=1 时偏差较大。为此,需对 x 2 进行连续性矫 正使之符合 x 2 的理论分布: ] ( . ) [ − − = E O E xc 2 2 0 5 当 df≥2 时,可以不作连续性矫正

&6.2适合性测验 根据x2分布的概率值来判断实际次数与预期理论次数是否符合的假设测 验,称为适合性测验(goodness test)。 测验实际结果与理论比例是否符合 测验产品质量是否合格: 测验实验结果是否符合某一理论分布: 【例7.1】孟德尔(1865)将黄子叶饱满豌豆与绿子叶皱缩豌豆杂交,下2代 观察556株,黄子叶饱满315株,黄子叶皱缩101株,绿子叶饱满108株,绿 子叶皱缩32株。试测验F2代的分离是否符合93:3:1的理论比率。 豌豆杂种F2代性状分离的观察次数与理论次数(=556) 次数 黄子叶饱满黄子叶皱缩绿子叶饱满绿子叶皱缩 实际次数(0)315 101 108 32 理论次数(E)312.75104.25 104.25 34.75 假设Ho:F2代的分离符合93:3:1的理论比率, 学 HA:F2代的分离不符合93:31的理论比率 显著水平a=0.05。 x-315-3275+01-10425,108-10425,62-3475 312.75 104.25 104.25 34.75 程 =0.470 dfk-1=41=3,由附表4查出x2o.0s.3=7.815。 x2<x305.3,不能否定H0,认为豌豆杂种F2代的分离是符合93:3:1 的理论比率。 【例7.2】有一批水稻种子,规定发芽率达80%合格,即发芽:不发芽=41 随机抽200粒做发芽试验,发芽种子数为150粒。这批水稻种子是否合格? 假设H0:合格,即发芽:不发芽=4:1 c-o~E外0 E _150-160-05+050-0-05-228 160 40 df=k-1=2-1=1,由附表4查出x2005.1=3.84 结论:xe2<x2o.o5.1,不能否定H0,认为这批水稻种子是合格的
4 教 学 过 程 &6.2 适合性测验 根据 x 2 分布的概率值来判断实际次数与预期理论次数是否符合的假设测 验,称为适合性测验(goodness test)。 测验实际结果与理论比例是否符合; 测验产品质量是否合格; 测验实验结果是否符合某一理论分布; 【例 7.1 】孟德尔(1865)将黄子叶饱满豌豆与绿子叶皱缩豌豆杂交,F2 代 观察 556 株,黄子叶饱满 315 株,黄子叶皱缩 101 株,绿子叶饱满 108 株,绿 子叶皱缩 32 株。试测验 F2 代的分离是否符合 9:3:3:1 的理论比率。 豌豆杂种 F2 代性状分离的观察次数与理论次数(n=556) 次数 黄子叶饱满 黄子叶皱缩 绿子叶饱满 绿子叶皱缩 实际次数(O) 315 101 108 32 理论次数(E) 312.75 104.25 104.25 34.75 假设 H0: F2 代的分离符合 9:3:3:1 的理论比率, HA: F2 代的分离不符合 9:3:3:1 的理论比率。 显著水平 a=0.05 。 ( ) ( ) ( ) ( ) 0 470 34 75 32 34 75 104 25 108 104 25 104 25 101 104 25 312 75 315 312 75 2 2 2 2 2 . . . . . . . . . = − + − + − + − x = df=k-1=4-1=3,由附表 4 查出 x 2 0.05,3 =7.815 。 x 2<x 2 0.05,3 ,不能否定 H0 ,认为豌豆杂种 F2 代的分离是符合 9:3:3:1 的理论比率。 【例 7.2 】有一批水稻种子,规定发芽率达 80%合格,即发芽:不发芽=4:1。 随机抽 200 粒做发芽试验,发芽种子数为 150 粒。这批水稻种子是否合格? 假设 H0:合格,即发芽:不发芽=4:1 ( ) ( ) ( ) 2 28 40 50 40 0 5 160 150 160 0 5 0 5 2 2 1 2 2 . . . . = − − + − − = − − = = k i i i i c E O E x df=k-1=2-1=1,由附表 4 查出 x 2 0.05,1 =3.84 。 结论:x c 2< x 2 0.05,1 ,不能否定 H0 ,认为这批水稻种子是合格的

例7.5大豆花色一对等位基因的遗传研究,以紫花和白花的大豆品种杂交, 在F2代共得289株,其中紫花208株,白花81株。问这一资料的实际观察比 例是否符合于3:1的理论比值。 解:Ho:大豆花色F2分离符合3:1比率 由于该资料只有k=2组,v=k-1=1,故在计算x值时需作连续性矫正 0-)-打 x2=∑ E _(1-875-0.5}(8.75l-0.5} =0.3140+0.9420=1.2560 216.75 72.25 查表:X2005d-1F3.841X20.01dr1=6.635 现x2=1.2560<.1,故应接受H0,说明大豆花色这对性状是符合3: 比率。 结论:大豆花色符合一对等位基因的表型分离比例。 教 例:据以往的调查,消费者对3种不同原料的的满意度分别为0.45,0.31 学0.24。现随机选择60人评定该3种不同原料的饮料。从中选出各自最喜欢的 产品,结果分别为30人,18人,12人,试问消费者对3个新产品的态度是否 过 有改变? Ho:无改变 =∑0-Er -0.871 E x2-0.871<xos(2)=5.99,接受H0 结论:消费者对3个新产品的态度没有改变。 &6.3独立性测验 独立性测验(independence test)是测验两个变数之间是相互独立还是彼此 相关的统计方法,是次数资料的一种相关研究。 X2独立性其步骤和方法是: Ho:两个变数相互独立,HA:两个变数彼此相关。 将资料按两向分组排列成r行、c列的相依表(表5.3) X2基本公式或变形公式计算值 按自由度dfr-1(c-l)查表进行x2测验 写统计结论
5 教 学 过 程 例 7.5 大豆花色一对等位基因的遗传研究,以紫花和白花的大豆品种杂交, 在 F2 代共得 289 株,其中紫花 208 株,白花 81 株。问这一资料的实际观察比 例是否符合于 3∶1 的理论比值。 解:H0:大豆花色 F2 分离符合 3∶1 比率。 由于该资料只有 k=2 组, = k − 1 = 1 ,故在计算 2 值时需作连续性矫正。 − − = E O E xc 2 2 ] 2 1 [( ) 0.3140 0.9420 1.2560 72.25 ( |8.75|-0.5) 216.75 ( |-8.75|-0.5)2 2 = + = + = 查表:χ 2 0.05(df=1)=3.841 χ2 0.01(df=1)=6.635 现 =1.2560 2 C < 2 0.05,1 ,故应接受 H0,说明大豆花色这对性状是符合 3∶1 比率。 结论:大豆花色符合一对等位基因的表型分离比例。 例:据以往的调查,消费者对 3 种不同原料的的满意度分别为 0.45,0.31, 0.24。现随机选择 60 人评定该 3 种不同原料的饮料。从中选出各自最喜欢的 产品,结果分别为 30 人,18 人,12 人,试问消费者对 3 个新产品的态度是否 有改变? H0:无改变 − = E O E xc 2 2 [( )] =0.871 x 2=0.871< (2) 5.99 2 x0.05 = ,接受 H0 结论:消费者对 3 个新产品的态度没有改变。 &6.3 独立性测验 独立性测验(independence test)是测验两个变数之间是相互独立还是彼此 相关的统计方法,是次数资料的一种相关研究。 X2 独立性其步骤和方法是: H0:两个变数相互独立,HA:两个变数彼此相关。 将资料按两向分组排列成 r 行、c 列的相依表(表 5.3)。 X2 基本公式或变形公式计算值 按自由度 df=(r-1)( c-1)查表进行 x 2 测验。 写统计结论

一、2×2联列表式经X2独立性测验 1.2×2表的一般形式 结果1 结果2 合计 外理1 处理2 a21 822 R2 合计 CI C2 n xfadz-anaal-n d=1 2.实例 例[7.8]调查经过种子灭菌处理与未经种子灭菌处理的小麦发生散黑穗病的穗 数,得相依表7.7,试分析种子灭菌与否和散黑穗病病穗多少是否有关。 表7.7防治小麦散黑穗病的观察结果 处理项目 发病穗数 未发病穗数 总数 种子灭菌 26(34.7) 50(41.3) 76 种子未灭菌 184(1753 200(2087】 384 总粉 210 250 460 解:假设:种子灭菌与否和散黑穗病病穗多少无关。 方法1:基本公式 程 Σ0-引 E =4.267 方法2: edal-nDF=1 CC2RR 026×200-184×501-406y×406 =4.267 210×250×76×384 x2=4.267>x20051=3.841差异显著。 结论:种子灭菌对防治小麦散黑穗病有一定效果。 二、2×c联列表式经X?独立性测验 1.2×c表的一般形式:
6 教 学 过 程 一、2×2联列表式经 X2独立性测验 1.2×2 表的一般形式: 结果 1 结果 2 合计 处理 1 处理 2 a11 a12 a21 a22 R1 R2 合计 C1 C2 n 1 (| | ) 1 2 1 2 2 2 11 22 12 21 2 = − − = df C C R R a a a a n x n C 2.实例 例[7.8]调查经过种子灭菌处理与未经种子灭菌处理的小麦发生散黑穗病的穗 数,得相依表 7.7,试分析种子灭菌与否和散黑穗病病穗多少是否有关。 表 7.7 防治小麦散黑穗病的观察结果 处理项目 发病穗数 未发病穗数 总数 种子灭菌 26(34.7) 50(41.3) 76 种子未灭菌 184(175.3) 200(208.7) 384 总数 210 250 460 解:假设:种子灭菌与否和散黑穗病病穗多少无关。 方法 1: 基本公式 − − = E O E xc 2 2 ] 2 1 [( ) =4.267 方法 2: 4.267 x 3.841 差异显著。 4.267 210 250 76 384 ) 406 2 406 (| 26 200 184 50 | , 1 (| | ) 0.05,1 2 2 2 1 2 1 2 2 1 1 2 2 1 2 2 1 2 2 = = = − − = = − − = C n C x DF C C R R a a a a n x 结论:种子灭菌对防治小麦散黑穗病有一定效果。 二、2×c 联列表式经 X2独立性测验 1. 2×c 表的一般形式:

纵行因素 横行因素 2 总计 e 1 a11 a12 RI 2 a22 a2c R2 C2 Ce n Df=(2-1c1c-1 [例7.9]进行大豆等位酶Aph的电泳分析,193份野生大豆、223份栽培 大豆等位基因型的次数列于表,试分析大豆Aph等位酶的等位基因型频率是 否因物种而不同! 物种 等位基因型 总计 野生大豆 29(23.66)68(123.87)96(45.47) 193 栽培大豆 22(27.34)199(143.13)2(52.53 223 总计 51 267 98 416 学 Ho:等位基因型频率与物种无关 H:两者有关,不同物种等位基因型频率不同 c n 4162「29268296219321 t-132司++8-6=15404 x2=154.04>x20.052=5.99,差异显著。 结论:不同物种的Aph等位基因型频率有显著差别。 三、r×c联列表式经X独立性测验 1.r×c表的一般形式: 纵行因素 横行因 2 c 总计 1 a12 alc R 2 a21 a22 a2c R arl ar2 arc 总计C1C2 Cc 公式:子=迈)-川 7
7 教 学 过 程 横行因素 纵行因素 总计 1 2 . c 1 2 a11 a12 a1c a21 a22 a2c R1 R2 总计 C1 C2 Cc n Df=(2-1)(c-1)=c-1 [例 7.9] 进行大豆等位酶 Aph 的电泳分析,193 份野生大豆、223 份栽培 大豆等位基因型的次数列于表,试分析大豆 Aph 等位酶的等位基因型频率是 否因物种而不同。 物种 等位基因型 总计 1 2 3 野生大豆 29(23.66) 68(123.87) 96(45.47) 193 栽培大豆 22(27.34) 199(143.13) 2(52.53) 223 总计 51 267 98 416 H0:等位基因型频率与物种无关 HA:两者有关,不同物种等位基因型频率不同 [ ] 2 1 2 1 1 2 2 2 = − n R c a R R n x i i 154.04 416 193 98 96 267 68 51 29 193 223 4162 2 2 2 2 = + + − = 2 x 2=154.04> x2 0.05(2) =5.99,差异显著。 结论:不同物种的 Aph 等位基因型频率有显著差别。 三、r×c 联列表式经 X2独立性测验 1. r×c 表的一般形式: 横行因素 纵行因素 1 2 . c 总计 1 2 ┊ R a11 a12 a1c R1 a21 a22 a2c R2 ┊ ┊ ┊ ┊ ar1 ar2 arc Rr 总计 C1 C2 Cc n 公式: [ ( ) 1] 2 2 = − i j ij r c a x n = [ − ] n R c a R R n x i i 2 1 2 1 1 2 2 2

[例7.10]表7.11为不同灌溉方式下水稻叶片衰老情况的调查资料。试测 验稻叶衰老情况是否与灌溉方式有关。 灌溉方式绿叶素黄叶素枯叶数总计 深水 146 7 160 浅水 183 13 205 湿润 152 14 16 182 计 481 30 36 547 H:稻叶衰老情况与灌溉方式无关 =∑巴 72 182×36-1.63 162 》 x2=5.63<x2054=9.49差异不显著。 结论:稻叶衰老情况与灌溉方式无关。 过 程三、总结与巩固 1.小结 统计假设测验小结 分析步骤: 1.资料属性 2.样本大小 3.比较项目 4.设计方法 计算:μ测验 T测验 X2测验 2.考核知识点 X2测验的基本公式及变形公式,X2适合性测验、X2独立性测验 3.考核要求 X2应用范围,X?适合性测验及2×2联列表X2独立性测验。 4.思考题 课堂练习: 通过对椰子两个品种受害虫的为害情况进行调查,A品种总共468株中有
8 教 学 过 程 [例 7.10] 表 7.11 为不同灌溉方式下水稻叶片衰老情况的调查资料。试测 验稻叶衰老情况是否与灌溉方式有关。 灌溉方式 绿叶素 黄叶素 枯叶数 总计 深 水 146 7 7 160 浅 水 183 8 13 205 湿 润 152 14 16 182 总 计 481 30 36 547 H0:稻叶衰老情况与灌溉方式无关 [ ( ) 1] 2 2 = − i j ij r c a x n ) 1 5.63 182 36 16 160 36 7 160 30 7 160 481 146 547 ( 2 2 2 2 = − + + + + 2 = 5.63 x 2 0.05,4 9.49 差异不显著。 2 xC = = 结论:稻叶衰老情况与灌溉方式无关。 三、总结与巩固 1.小结 统计假设测验小结 分析步骤: 1.资料属性 2.样本大小 3.比较项目 4.设计方法 计算:μ 测验 T测验 X2 测验 2.考核知识点 X2 测验的基本公式及变形公式,X2 适合性测验、X2 独立性测验 3.考核要求 X2 应用范围,X2 适合性测验及 2×2 联列表X2 独立性测验。 4.思考题 课堂练习: 通过对椰子两个品种受害虫的为害情况进行调查,A 品种总共 468 株中有

313株受害,B品种总共138株中有17株受害,分析不同品种的受害率是否存 在显著差异。 d)nDF=1 学 026×200-184×501 4062×406 过 210×250×76×384 =4.267 xc2=4.267>x20s1=3.841差异显著。 作业:P1433,4.6,7 通过社会学、遗传学、生物学等相关的通俗易懂实例来讲解卡平方测验应 用,学生很易掌握计数资料的适合性测验和独立性测验。到了教学目标要求, 记
9 教 学 过 程 313 株受害,B 品种总共 138 株中有 17 株受害,分析不同品种的受害率是否存 在显著差异。 作业:P143 3,4,6,7 教 学 后 记 通过社会学、遗传学、生物学等相关的通俗易懂实例来讲解卡平方测验应 用,学生很易掌握计数资料的适合性测验和独立性测验。到了教学目标要求。 4.267 x 3.841 差异显著。 4.267 210 250 76 384 ) 406 2 406 (| 26 200 184 50 | , 1 (| | ) 0.05,1 2 2 2 1 2 1 2 2 2 11 22 12 21 2 = = = − − = = − − = C n C x DF C C R R a a a a n x