章 第三章试验资料的整理及特征数 课时 5 节 3.1常用的统计术语 &3.2试验资料的性质与分类 3.3试验资料的整理(次数分布)&3.4试验资料的特征数 了解总体与样本、参数与统计数等常用统计术语的概念和试验资料的分类 教学 (②)掌握次数分布表和次数分布图的制作方法:(3)掌握平均数和变异数的意义 目的 (4)熟练借助计算器统计功能计算常用的统计量。 教学 重点掌握平均数、标准差、方差、平方和、标准差、标准误、变异系数的 重点 统计学意义及计算。 理解平均数与变异数作用的区别,反映资料变异程度稳中各统计量的意义, 尤其区别标准差与标准误的作用。 教学 突出方法: 难点 反复举科研实例说明反映资料集中性与变异性统计量的统计学意义与功用 区别。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钩主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中因林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985: 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7.《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9.《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10.《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002. 11.《试验设计与分析》,袁志发主编,高等教育出版社,2000
1 章 第三章 试验资料的整理及特征数 课时 5 节 &3.1 常用的统计术语 &3.2 试验资料的性质与分类 &3.3 试验资料的整理(次数分布) &3.4 试验资料的特征数 教学 目的 了解总体与样本、参数与统计数等常用统计术语的概念和试验资料的分类; (2)掌握次数分布表和次数分布图的制作方法;(3)掌握平均数和变异数的意义。 (4)熟练借助计算器统计功能计算常用的统计量。 教学 重点 重点掌握平均数、标准差、方差、平方和、标准差、标准误、变异系数的 统计学意义及计算。 教学 难点 理解平均数与变异数作用的区别,反映资料变异程度稳中各统计量的意义, 尤其区别标准差与标准误的作用。 突出方法: 反复举科研实例说明反映资料集中性与变异性统计量的统计学意义与功用 区别。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 11. 《试验设计与分析》,袁志发主编,高等教育出版社,2000

教师授课思路、设问及讲解要点 一、引言 如何从实践的偶然现象来提神事物存在的本质,通过科学试验的观察、测定和 记载,可以得到大量的数据资料。对于这些资料,必须按照一定的程序进行整理和 分析,才能透过数据表现看到蕴藏在数据中的客观规律。所以,资料的整理和分机 是试验工作的重要组成部分,也是深入认识客观事物的一个重要步骤。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &3.1常用的统计术语 一、总体(population)和样本(sample) 总体 总体 . .X,样本 学 观察以后 样本↓实现 过 样本值1样本值2 图1-2- 总体与样本 程 1.总体:据研究目的确定的研究对象的全体, 个体:总体中的一个研究单位称个体(individual). 总体分:有限总体和无限总体。 2.样本:总体的一部分称为样本。 样本容量:样本中所包含的个体数目叫样本容量(sample size)。常记为n。 通常n≤30的样本叫小样本,n>30的样本叫大样本。 3.为什么要随机抽样? (1)集团个体数多或无限 (2)有些是破坏性的试验 随机样本(random sample):非随机样本(non-random sample)。 4.总体与样本的关系 样本是集团的缩影,但不等于集团,抽样是一种手段 统计分析的核心在于由样本的情况推断集团的信息,保证一定精确度、可靠度。 由样本推断总体虽然有很大可靠性,也有一定错误率。俗语说“不可不信,不可全 信”,这是我们对待统计推断的正确态度
2 教 学 过 程 教师授课思路、设问及讲解要点 一、引言 如何从实践的偶然现象来提神事物存在的本质,通过科学试验的观察、测定和 记载,可以得到大量的数据资料。对于这些资料,必须按照一定的程序进行整理和 分析,才能透过数据表现看到蕴藏在数据中的客观规律。所以,资料的整理和分析 是试验工作的重要组成部分,也是深入认识客观事物的一个重要步骤。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &3.1 常用的统计术语 一、总体(population)和样本(sample) 1.总体:据研究目的确定的研究对象的全体. 个体:总体中的一个研究单位称个体(individual)。 总体分:有限总体和无限总体。 2.样本:总体的一部分称为样本。 样本容量:样本中所包含的个体数目叫样本容量(sample size)。常记为 n。 通常 n≤30 的样本叫小样本,n>30 的样本叫大样本。 3.为什么要随机抽样? (1)集团个体数多或无限 (2)有些是破坏性的试验 随机样本(random sample); 非随机样本(non-random sample)。 4.总体与样本的关系 样本是集团的缩影,但不等于集团,抽样是一种手段。 统计分析的核心在于由样本的情况推断集团的信息,保证一定精确度、可靠度。 由样本推断总体虽然有很大可靠性,也有一定错误率。俗语说“不可不信,不可全 信”,这是我们对待统计推断的正确态度

二、变数与变量 每一个体的某一性状、特性的测定数值叫做观察值(observation) 观察值集合起来,称为变数(variable) 变数中的每一成员称为变量(variate) 随机变数(mm一domvariable) 三、参数与统计数 L.参数(parameter):用总体的全体观察值计算的、描述总体的特征数称为参 数。 如:总体平均数- 总体方差-62 2.统计数(statistics):由样本的全体观察值计算的、描述样本的特征数。 如:样本平均数-一x 样本均方一 统计上,通常由样本统计数估计或推断总体相应参数。 &3.2试验资料的性质与分类 教 试验资料分两大类:数量性状资料和质量性状资料 1、数量性状资料 学 凡是能够以量测或计数的方法表示其特征的性状统称为数量性状。 观察测定数量性状而获得的数据就是数量性状资料,分为(1)计量资料(②)计 过 数资料。 (1)计量资料 程 凡用称量、测量等量测手段得到的数量性状资料。 各个观察值不一定是整数,两个相邻的整数间可有带小数的任何数值出现:计 量资料也称之为连续性变异资料. (2)计数资料 指用计数方式得到的数据资料, 它的各个观察值须以整数表示,两个相邻整数间不容许任何带有小数的值存 在。因此,该类资料也称非连续性变异资料或称间断性资料。 2、质量性状资料 质量性状是指只能观察而不能测量的性状。 如花药、茎、种子、果实、叶片的颜色、籽粒的饱满度、芒的有无等。 质量性状本身不能用数值表示,要获得这类性状的资料,须对其观察结果作数 量化处理。 数量化方法可分两种: (1)统计次数法 (2)分级法 (1)统计次数法 在一个样本内,分别统计具有某种性状、不具有该性状的个体数,这种数量化的资 料又叫次数资料
3 教 学 过 程 二、变数与变量 每一个体的某一性状、特性的测定数值叫做观察值(observation)。 观察值集合起来,称为变数(variable) 变数中的每一成员称为变量(variate) 随机变数(mn—domvariable) 三、参数与统计数 1.参数(parameter): 用总体的全体观察值计算的、描述总体的特征数称为参 数。 如:总体平均数 -μ 总体方差- 2 2.统计数(statistics):由样本的全体观察值计算的、描述样本的特征数。 如:样本平均数- x 样本均方- 2 s 统计上,通常由样本统计数估计或推断总体相应参数。 &3.2 试验资料的性质与分类 试验资料分两大类:数量性状资料和质量性状资料 1、数量性状资料 凡是能够以量测或计数的方法表示其特征的性状统称为数量性状。 观察测定数量性状而获得的数据就是数量性状资料,分为(1)计量资料 (2)计 数资料 。 (1)计量资料 凡用称量、测量等量测手段得到的数量性状资料。 各个观察值不一定是整数,两个相邻的整数间可有带小数的任何数值出现;计 量资料也称之为连续性变异资料. (2)计数资料 指用计数方式得到的数据资料. 它的各个观察值须以整数表示,两个相邻整数间不容许任何带有小数的值存 在。因此,该类资料也称非连续性变异资料或称间断性资料。 2、质量性状资料 质量性状是指只能观察而不能测量的性状。 如花药、茎、种子、果实、叶片的颜色、籽粒的饱满度、芒的有无等。 质量性状本身不能用数值表示,要获得这类性状的资料,须对其观察结果作数 量化处理。 数量化方法可分两种: (1)统计次数法 (2)分级法 (1)统计次数法 在一个样本内,分别统计具有某种性状、不具有该性状的个体数,这种数量化的资 料又叫次数资料

例如 1.调查国光苹果的裂果情况 2.一个玉米果穗上甜粒与非甜粒的比率, (2)分级法 先根据性状的变异情况分级,给每级分别赋予一个适当的数值作代表值,然 后统计样本中属于各个级别的个体数。 例如调查作物受某种病虫害危害情况,将作物性状分为高抗、抗、中抗、中 感、感病5个级别,分别用1,2,3,4,5表示,统计样本内各种级别的植株数 &3.3试验资料的整理 试验资料整理为次数分布 次数分布:由不同区间内变量的次数组成的分布。 次数分布功用:整理资料、化繁为简:初步了解变数的分布特点:便于进一步 的计算和分析。 将次数分布作成表格形式叫次数分布表,次数分布以图来表示叫次数分布图。 教 一、次数分布表 (一)计量资料的次数分布表 计量资料在分组前需要确定组数、组距、各组中值及组限,然后将全部观测值 计数归组。 过 书例p38以表3.4的140行水稻试验的产量为例,说明整理方法。 表3.4140行水稻产量(单位:克) 程 17721519797123159245119119131149152167104 16121412517521911819217617595136199116 165 21495 158 8313780 138151187126 196134206 137 98 97129143179174159165136108 101141148 16s 16317610219414517375130149 150161 15111 158 131189 91 142140154 152163 123 205 15 131 209 18397 119181149187 131215111 186 118 150 155 116 254 239160172179 151198124 179 184 168 169 173 181 188 211 197175 122151 171166 175 143 190 213 192231163159158159177147194227141169124159 L.数据排序(sort) 2.求极差(range):极差为254-75=179g 3.确定组数和组距(class interval) 应考虑: (1)观察值个数的多少:(2)极差的大小:(3)便于计算: (4)能反映出资料的真实面貌等方面
4 教 学 过 程 例如 1.调查国光苹果的裂果情况; 2.一个玉米果穗上甜粒与非甜粒的比率。 (2)分级法 先根据性状的变异情况分级,给每级 分别赋予一个适当的数值作代表值,然 后统计样本中属于各个级别的个体数。 例如 调查作物受某种病虫害危害情况,将作物性状分为高抗、抗、中抗、中 感、感病 5 个级别,分别用 1,2,3,4,5 表示,统计样本内各种级别的植株数。 &3.3 试验资料的整理 试验资料整理为次数分布 次数分布:由不同区间内变量的次数组成的分布。 次数分布功用:整理资料、化繁为简;初步了解变数的分布特点;便于进一步 的计算和分析。 将次数分布作成表格形式叫次数分布表,次数分布以图来表示叫次数分布图。 一、次数分布表 (一)计量资料的次数分布表 计量资料在分组前需要确定组数、组距、各组中值及组限,然后将全部观测值 计数归组。 书例 p38 以表 3.4 的 140 行水稻试验的产量为例,说明整理方法。 表 3.4 140 行水稻产量(单位:克) 177 215 197 97 123 159 245 119 119 131 149 152 167 104 161 214 125 175 219 118 192 176 175 95 136 199 116 165 214 95 158 83 137 80 138 151 187 126 196 134 206 137 98 97 129 143 179 174 159 165 136 108 101 141 148 168 163 176 102 194 145 173 75 130 149 150 161 155 111 158 131 189 91 142 140 154 152 163 123 205 149 155 131 209 183 97 119 181 149 187 131 215 111 186 118 150 155 197 116 254 239 160 172 179 151 198 124 179 135 184 168 169 173 181 188 211 197 175 122 151 171 166 175 143 190 213 192 231 163 159 158 159 177 147 194 227 141 169 124 159 1. 数据排序(sort) 2. 求极差(range) :极差为 254-75=179g。 3. 确定组数和组距(class interval) 应考虑: (1)观察值个数的多少; (2)极差的大小;(3)便于计算; (4)能反映出资料的真实面貌等方面

表3.5样本容量与组数多少的关系 祥本内观察值的个数 分组时的组数 5-10 8-16 10-20 12-24 组距:1=R/组数为了便于计算,组距一般取整数。 本例R=179,分为12组,故组距:(1)=179/12=14.9≈15(g) 4.确定组中值与组限 组中值(组值,class value)是各组区间的中点值,它可作为各组的代表值 最好取整数或与观察值位数一致。一般先确定第一组的组中值,通常选接近资料中 最小观察值为宜。 本例:12个组中值分别为:75,90,105,.,255 教 组限(class1imit):各组的界限。下限为该组中值减去1/2组距,上限为组 中值加1/2组距 学 第一组的下限=75-(15/2)=67.5g 过 上限=75+(15/2)=82.5g 即:第一组的组限为67.5一82.5g 程 5.原始资料归组 表3.6140行水稻的次数分布 组限 中点值次数 67.5-82.5 76 2 一97.5 127.5-142.5 13 142.5-157.5 20 157.5-172.5 172 一18. 187.217.5 39 217.5925 3 232.5-247.5 240 2 247.5-262.5 255 合计(n) 140 5
5 教 学 过 程 表 3.5 样本容量与组数多少的关系 样本内观察值的个数 分组时的组数 50 100 200 300 500 1000 5—10 8—16 10—20 12—24 15—30 20—40 组距: i=R/组数 为了便于计算,组距一般取整数。 本例 R=179,分为 12 组,故组距: (i)=179/12=14.9≈15(g) 4. 确定组中值与组限 组中值(组值,class value)是各组区间的中点值,它可作为各组的代表值, 最好取整数或与观察值位数一致。一般先确定第一组的组中值,通常选接近资料中 最小观察值为宜。 本例:12 个组中值分别为: 75,90 , 105, ., 255 组限(class limit):各组的界限。下限为该组中值减去 1/2 组距,上限为组 中值加 1/2 组距。 第一组的下限=75-(15/2)=67.5g 上限=75+(15/2)=82.5g 即:第一组的组限为 67.5—82.5g . 5.原始资料归组 表 3.6 140 行水稻的次数分布 组 限 中点值 ( y ) 次数 67.5— 82.5 75 (2f ) 82.5— 97.5 90 7 97.5—112.5 105 7 112.5—127.5 120 13 127.5—142.5 135 17 142.5—157.5 150 20 157.5—172.5 165 25 172.5—187.5 180 21 187.5—202.5 195 13 202.5—217.5 210 9 217.5—232.5 225 3 232.5—247.5 240 2 247.5—262.5 255 1 合计( n ) 140

(二)计数资料的次数分布表 变异较小的资料,可按观察值分组. 例如p37:某小麦品种的每穗小穗数的次数分布 变异较大的计数资料,可用处理计量资料的方法制作次数分布表。 【例如】研究水稻品种的每穗粒数,共测200个穗,每穗粒数的变幅在27-83,极 差达56。 表3.3200个稻穗每穗粒数的次数分布表 每穗粒数(y)次数(仰稳数) 26-30 1 3135 36-40 41-45 46-50 32 51一55 41 56-60 教 61-65 66一70 16 学 71-75 8 76-80 3 81-852 过 合计 200 (三)质量性状资料的次数分布表 程 例如,用某微肥处理后,红星苹果果实着色情况调查,见下表。 果实者色分级 代表值 果实数 全红 5 14 )2/3果面红色 4 36 1/3-2/3果面红色 3 97 <1/3果面红色 2 53 全绿 1 7 二、次数分布图 次数分布图可以更形象地表明次数分布的情况, 常用:方柱形图、多边形图、条形图和饼图。 (一)柱形图(直方图,histogram) 适用于表示连续性变异资料的次数分布
6 教 学 过 程 (二)计数资料的次数分布表 变异较小的资料,可按观察值分组. 例如 p37:某小麦品种的每穗小穗数的次数分布 变异较大的计数资料,可用处理计量资料的方法制作次数分布表。 【例如】研究水稻品种的每穗粒数,共测 200 个穗,每穗粒数的变幅在 27-83,极 差达 56。 表 3.3 200 个稻穗每穗粒数的次数分布表 每穗粒数( y ) 次数(即穗数 f) 26—30 1 31—35 3 36—40 10 41—45 21 46—50 32 51—55 41 56—60 38 61—65 25 66—70 16 71—75 8 76—80 3 81—85 2 合计 200 (三)质量性状资料的次数分布表 例如,用某微肥处理后,红星苹果果实着色情况调查,见下表。 果实着色分级 代表值 果实数 全红 >2/3 果面红色 1/3-2/3 果面红色 <1/3 果面红色 全绿 5 4 3 2 1 14 36 97 53 7 二、次数分布图 次数分布图可以更形象地表明次数分布的情况。 常用:方柱形图、多边形图、条形图和饼图。 (一)柱形图(直方图,histogram) 适用于表示连续性变异资料的次数分布
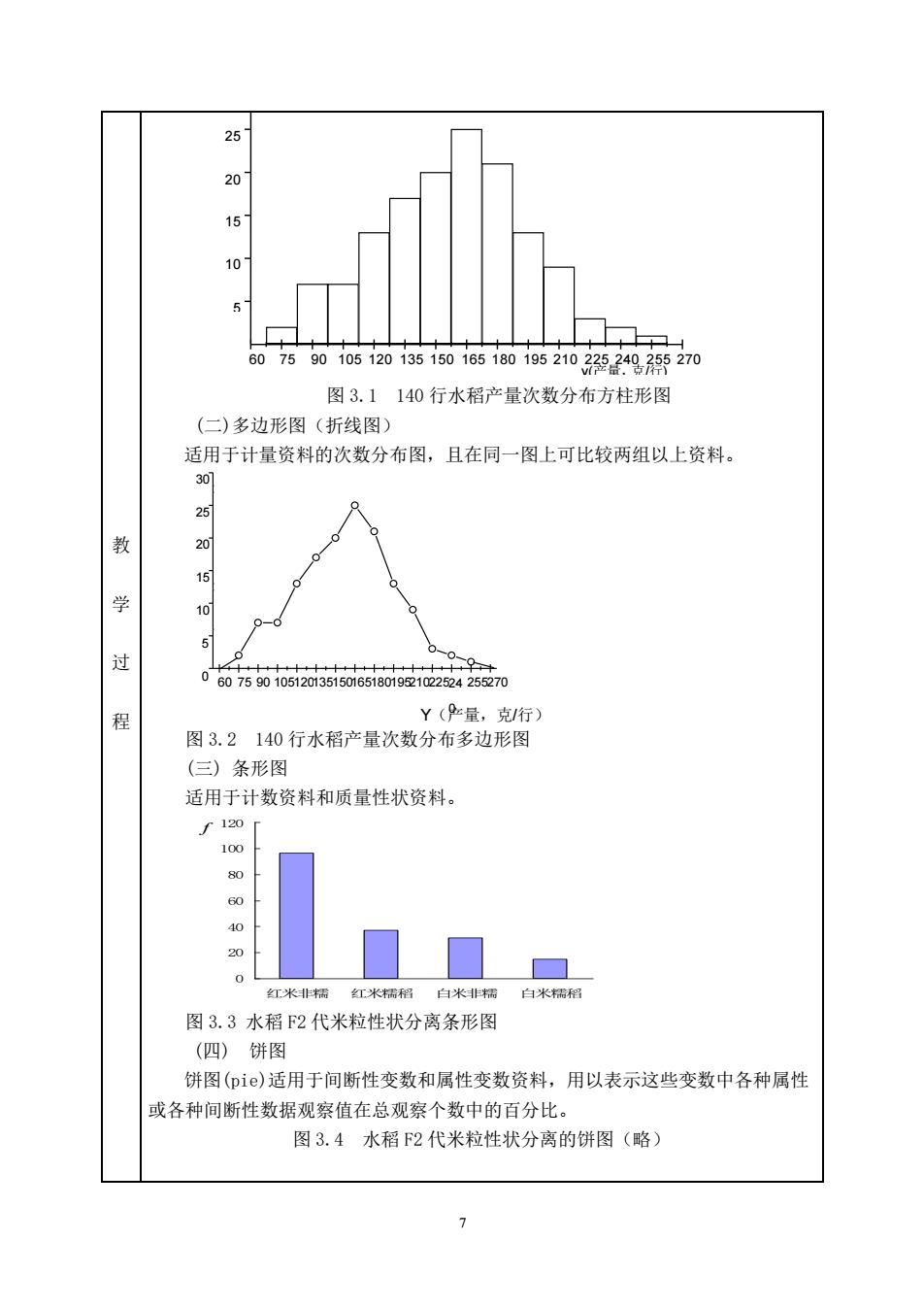
20 15 607901051201351501651801952103249,5270 图3.1140行水稻产量次数分布方柱形图 (二)多边形图(折线图) 适用于计量资料的次数分布图,且在同一图上可比较两组以上资料。 30 15 过 06o6t0i05i2o35i5o65ieoi9过12a42动0 程 Y(量,克行) 图3.2140行水稻产量次数分布多边形图 (三)条形图 适用于计数资料和质量性状资料。 r120 20 红米糯红米相自米非锅自米相 图3.3水稻F2代米粒性状分离条形图 (四))饼图 饼图(pi©)适用于间断性变数和属性变数资料,用以表示这些变数中各种属性 或各种间断性数据观察值在总观察个数中的百分比。 图3.4水稻下2代米粒性状分离的饼图(略) 7
7 教 学 过 程 图 3.1 140 行水稻产量次数分布方柱形图 (二)多边形图(折线图) 适用于计量资料的次数分布图,且在同一图上可比较两组以上资料。 图 3.2 140 行水稻产量次数分布多边形图 (三) 条形图 适用于计数资料和质量性状资料。 0 20 40 60 80 100 120 红米非糯 红米糯稻 白米非糯 白米糯稻 f 图 3.3 水稻 F2 代米粒性状分离条形图 (四) 饼图 饼图(pie)适用于间断性变数和属性变数资料,用以表示这些变数中各种属性 或各种间断性数据观察值在总观察个数中的百分比。 图 3.4 水稻 F2 代米粒性状分离的饼图(略) 60 75 90 105 120 135 150 165 180 195 210 225 240 255 270 5 10 15 20 25 y(产量,克/行) 60 75 90 10512013515016518019521022524 0 255270 0 5 10 15 20 25 30 Y(产量,克/行)

&2.4试验资料的特征数 资料整理得的次数分布表、图,形象直观地反映了资料两特点:集中性和离散 性 现介绍用更简单、精确的统计量来反映。 一、反应资料集中性的特征数 ·平均数 二、反应其离散性的特征数一一一变异数 三、反应抽样误差的特征数 一标准误 一、平均数 平均数种类较多常用的有:算术平均数、几何平均数、中位数、众数。 应用最普遍的是算术平均数。 平均数功用:是数量资料的代表数,可综合反映研究对象在一定条件下形成的 般水平,常用来进行资料间的比较。 (一)算术平均数 各个观察值的总和除以观察值个数所得的商,称为算术平均数(arithmetic 教 mean),简称平均数。 通常用μ表示总体平均数,下表示样本平均数。 学 过 因为总体内的个体数很多,总体平均数往往无从计算,所以,一般用样本平均 作为总体平均数μ的估计值。 程 设有一个容量为n的样本,其观察值为x,x2,x。,则该样本的算术平均数可 定义为: 从总体中抽出的随机样本平均数x是该总体平均数μ的无偏估计值。 平均数的基本性质: A离均差代数和为零。即:∑(x-)=0 B.离均差平方之和为最小值。∑(x-)2<∑(x-a)(注:a≠) 平均数功用:作为数量资料的代表值,表示资料中变量的中心位置,并作为资料的 代表,与其他资料进行比较。 计算方法: (1)直接算法直接法 各个观察值的总和除以观察值个数所得的商
8 教 学 过 程 &2.4 试验资料的特征数 资料整理得的次数分布表、图,形象直观地反映了资料两特点:集中性和离散 性,现介绍用更简单、精确的统计量来反映。 一、反应资料集中性的特征数——— 平均数 二、反应其离散性的特征数——— 变异数 三、反应抽样误差的特征数——— 标准误 一、平均数 平均数种类较多常用的有:算术平均数、几何平均数、中位数、众数。 应用最普遍的是算术平均数。 平均数功用:是数量资料的代表数,可综合反映研究对象在一定条件下形成的 一般水平,常用来进行资料间的比较。 (一)算术平均数 各个观察值的总和除以观察值个数所得的商,称为算术平均数(arithmetic mean),简称平均数。 通常用μ表示总体平均数, x 表示样本平均数。 N x N x N x x x N i i N = = + + + = 1 2 =1 . 因为总体内的个体数很多,总体平均数往往无从计算,所以,一般用样本平均 数 作为总体平均数μ的估计值。 设有一个容量为 n 的样本,其观察值为 n x , x ., x 1 2 ,则该样本的算术平均数可 定义为: n x n x n x x x x n i i n = = + + + = 1 2 =1 . 从总体中抽出的随机样本平均数 x 是该总体平均数μ的无偏估计值。 平均数的基本性质: A.离均差代数和为零。即: (x − x) = 0 B.离均差平方之和为最小值。 ( ) ( ) ( ) 2 2 x − x x − a 注:a x 平均数功用:作为数量资料的代表值,表示资料中变量的中心位置,并作为资料的 代表,与其他资料进行比较。 计算方法: (1)直接算法直接法 各个观察值的总和除以观察值个数所得的商。 n x x =

(2)加权法 对己归组的资料,其计算公式为: +色. f+5+.+f n 其中:xi一各组组中值:k一组数: n一资料中所有观察值的个数 fi一各组次数: 【例2.2】在一水稻品种比较试验中,某品种的5个小区产量分别为20.0, 19.0,21.0,17.5,18.5kg),求该品种的小区产量平均数。 s∑x (20.0+19.0+21.0+17.5+18.5)/5=19.2(kg) n 【例2.3】利用加权法求100株湘菊梨单株产量的算术平均数 教 =(48.5×3+51.5×6++69.5×7+72.5×4)/100= 学60.92(kg) (二)中数(Md) 过 将观察值按大小依次排列,当观察值数目为奇数时,最中间的观察值就是中数 当观察值数目为偶数时,最中间的两个观察值的算术平均数为中数。 程 如2,2,3,4,7,8,9,11,14:5,7,8,9,10,11: (三)众数(M0) 在资料中出现次数最多的数或组中值。 如某一调查结果为:34,3,3,5,6,4,3,2,2 (四)几何平均数(Mg) 设有n个观察值,其乘积开n次方所得的值,即为几何平均数,即 Mg=xx.x=Ig(Igx n) 二、变异数 (一)极差(R) 它由两个极端观察值决定,受资料中不正常的极端值的影响大,没有充分利用 资料的全部信息,不能精确表示资料的变异度。 (仁)方差与标准差 1.引入标准差的必要性 每个观察值与平均数之差即离均差;表示观察值偏离平均数的距离。 离均差的平方再求和简称平方和(sum of square),记为SS
9 教 学 过 程 (2)加权法 对已归组的资料,其计算公式为: n f x f f f f x f x f x x k i i i k k k = = + + + + + + = 1 1 2 1 1 2 2 . . 其中: xi—各组组中值;k—组数; n —资料中所有观察值的个数; fi —各组次数; 【例 2.2】在一水稻品种比较试验中,某品种的 5 个小区产量分别为 20.0, 19.0,21.0,17.5,18.5(kg),求该品种的小区产量平均数。 n x x = =(20.0+19.0+21.0+17.5+18.5)/5= 19.2(kg) 【例 2.3】利用加权法求 100 株湘菊梨单株产量的算术平均数。 n f x x k i i i = = 1 =(48.5×3+51.5×6+.+69.5×7+72.5×4)/100= 60.92(kg) (二) 中数(Md) 将观察值按大小依次排列,当观察值数目为奇数时,最中间的观察值就是中数; 当观察值数目为偶数时,最中间的两个观察值的算术平均数为中数。 如 2,2,3,4,7,8,9,11,14; 5,7,8,9,10,11; (三) 众数( M0 ) 在资料中出现次数最多的数或组中值。 如某一调查结果为: 3,4,3,3,5,6,4,3,2,2 (四) 几何平均数( Mg ) 设有 n 个观察值,其乘积开 n 次方所得的值,即为几何平均数,即 二、变异数 (一) 极差(R) 它由两个极端观察值决定,受资料中不正常的极端值的影响大,没有充分利用 资料的全部信息,不能精确表示资料的变异度。 (二) 方差与标准差 1.引入标准差的必要性 每个观察值与平均数之差即离均差;表示观察值偏离平均数的距离。 离均差的平方再求和简称平方和(sum of square),记为 SS。 − Mg = x .x .x = lg ( lg x / n) i n n 1 1 2

对总体:s-2-r-Σr.酒 对样本:=∑K-=∑r∑ 平方和:刻画所有数据偏离中心的总变异量。 平方和(SS)的大小受观察值个数影响。为消除SS的这个缺陷,可将SS除以观察信 的个数得到平均平方和,称之为方差(variance)。 总体方差等于总体平方和除以总体观察值个数N,用表示,即: 总体方差通常无法得到,而由样本方差估计,样本方差称为均方(mean square) 记为 或s:g=2x-∑r-∑划 SS n-1 n-1 上式中的(m-l)称为自由度(degree of freedom),简记为df。它是指样本内能 教 独立自由变动观察值的个数。 【例2.4】有5个观察值,其中4个观察值的离均差为3,-2,3,5,那么第 学 个观察值的离均差必为-9,才能满足:∑(x-)=0 在估计其他统计数时,如该统计数受k个条件限制,则自由度等于样本观察值 过 个数减去约束条件数k,即样本自由度为-k。 2,标准差的定义与计算式 程 统计学上把方差或均方的平方根取正值称为标准差。 总体标准差:σ= ∑(x-2 ∑x2-∑x21N N 样本标准差:s= ∑(x-2 ∑x2-(∑x21n n-1 n-1 标准差的功用:衡量资料的变异性,估计试验误差。S:刻画平均到每一独立数据 的变异度. 例:表2.7某水稻品种小区产量的方差和标准差的计算20.0,19,21,17.5,18.5。 ∑-73-1825g n-1 4 x-2 s=2n-1 -1351 V4
10 教 学 过 程 对总体: 2 2 2 ( ) ( ) N x SS x x = − = − 对样本: 2 2 2 ( ) ( ) n x ss x x x = − = − 平方和:刻画所有数据偏离中心的总变异量。 平方和(SS)的大小受观察值个数影响。为消除 SS 的这个缺陷,可将 SS 除以观察值 的个数得到平均平方和,称之为方差 (variance)。 总体方差等于总体平方和除以总体观察值个数 N,用 表示,即: 总体方差通常无法得到,而由样本方差估计,样本方差称为均方 (mean square) 记为 或 MS : df SS n n x x n x x s = − − = − − = 1 ( ) 1 ( ) 2 2 2 2 上式中的(n-1)称为自由度(degree of freedom),简记为 df。它是指样本内能 独立自由变动观察值的个数。 【例 2.4】 有 5 个观察值,其中 4 个观察值的离均差为 3,-2,3,5,那么第 5 个观察值的离均差必为-9,才能满足: (x − x) = 0 在估计其他统计数时,如该统计数受 k 个条件限制,则自由度等于样本观察值 个数减去约束条件数 k,即样本自由度为 n-k。 2.标准差的定义与计算式 统计学上把方差或均方的平方根取正值称为标准差。 总体标准差: N x x N N (x ) ( / 2 2 )2 = − = − 样本标准差: 1 ( / 1 ( ) 2 2 2 − − = − − = n x x n n x x s ) 标准差的功用:衡量资料的变异性,估计试验误差。S: 刻画平均到每一独立数据 的变异度. 例:表 2.7 某水稻品种小区产量的方差和标准差的计算 20.0,19,21,17.5,18.5。 2 2 2 1.825( ) 4 7.3 1 ( ) k g n x x s = = − − = 1.351 4 7.3 1 ( ) 2 = = − − = n x x s