
第十章直线回归与相关分析 &10.1 回归和相关分析概述 &10.2直线回归分析 &10.3直线相关分析 I 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 第十章 直线回归与相关分析 &10.1 回归和相关分析概述 &10.2 直线回归分析 &10.3 直线相关分析

&10.1 回归和相关分析概述 变量间的关系分为两类: 函数关系:完全确定性的关系一可用精确的数学式来 表示; 统计关系:不存在完全确定性的关系一不能用精确的 数学式来表示。 统计关系这一类变量间的关系就是统计学中回归分析与 相关分析所要讨论的问题。 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 &10.1 回归和相关分析概述 一、变量间的关系分为两类: 函数关系:完全确定性的关系——可用精确的数学式来 表示; 统计关系:不存在完全确定性的关系——不能用精确的 数学式来表示。 统计关系这一类变量间的关系就是统计学中回归分析与 相关分析所要讨论的问题

二、回归、相关分析的任务与类型 常用x、y来表示两个变量,(x,y)的各对观察值用 (x1,y1),(x2,y2),(x,yn)表示。 在统计上,x和y变量的关系有两种理论模型: 回归模型和相关模型。 回归模型(因果关系)中: x表示原因的变量;y是表示结果的变量。 回归分析目的:导出由x来预测或控制y的回归方程, 即确定当自变量x为某一值时依变量y将会在什么范围内 变化
常用x、y来表示两个变量,(x,y)的各对观察值用 (x1,y1),(x2,y2),.,(xn,yn)表示。 在统计上,x和y变量的关系有两种理论模型: 回归模型和相关模型。 回归模型(因果关系)中: x表示原因的变量;y是表示结果的变量。 回归分析目的:导出由x 来预测或控制y的回归方程, 即确定当自变量x为某一值时依变量y将会在什么范围内 变化。 二、回归、相关分析的任务与类型

>在相关模型中,其x和y变量是平行变化 关系,不能区别哪一个是自变量,哪一个 是依变量。 >相关分析目的:确定两个变量在数量关 系上的密切程度和性质。不能用一个或多 个变量去预测、控制另一个变量的变化
➢在相关模型中,其x和y变量是平行变化 关系,不能区别哪一个是自变量,哪一个 是依变量。 ➢相关分析目的:确定两个变量在数量关 系上的密切程度和性质。不能用一个或多 个变量去预测、控制另一个变量的变化

回归分析的类型: 一元回归分析(直线和曲线回归分析); 多元回归分析(多元线性回归分析和曲面 回归分析)。 相关分析的类型:直线相关分析; 复相关分析。 偏相关分析
回归分析的类型: 一元回归分析(直线和曲线回归分析); 多元回归分析(多元线性回归分析和曲面 回归分析)。 相关分析的类型:直线相关分析; 复相关分析。 偏相关分析

三、两个变数资料的散点图 >对具有统计关系的两个变数的资料进行初步考察 的简便而有效的方法,是将这两个变数的n对观 察值(x1,y1)、(x2,y2)、(xn,yn)分别以 坐标点的形式标记于同一直角坐标平面上,获得 散点图(scatter diagram)。 例如:
三、两个变数资料的散点图 ➢ 对具有统计关系的两个变数的资料进行初步考察 的简便而有效的方法,是将这两个变数的n对观 察值(x1,y1)、(x2,y2)、.、(xn,yn)分别以 坐标点的形式标记于同一直角坐标平面上,获得 散点图(scatter diagram)。 例如:

根据散点图可初步判定双变数和间的关系: >①X和Y相关的性质(正或负)和密切程度 >②X和Y的关系是直线型的还是非直线型的 >③是否有一些特殊的点表示着其他因素的干扰 网
根据散点图可初步判定双变数X和Y间的关系: ➢ ①X和Y相关的性质(正或负)和密切程度 ➢ ②X和Y的关系是直线型的还是非直线型的 ➢ ③是否有一些特殊的点表示着其他因素的干扰

&10.2直线回归分析 一、直线回归方程的建立 二、直线回归的显著性检验 三、直线回归的区间估计 可 海南大学农学院 唐燕琼制
海南大学农学院 唐燕琼制 &10.2 直线回归分析 一、直线回归方程的建立 二、直线回归的显著性检验 三、直线回归的区间估计
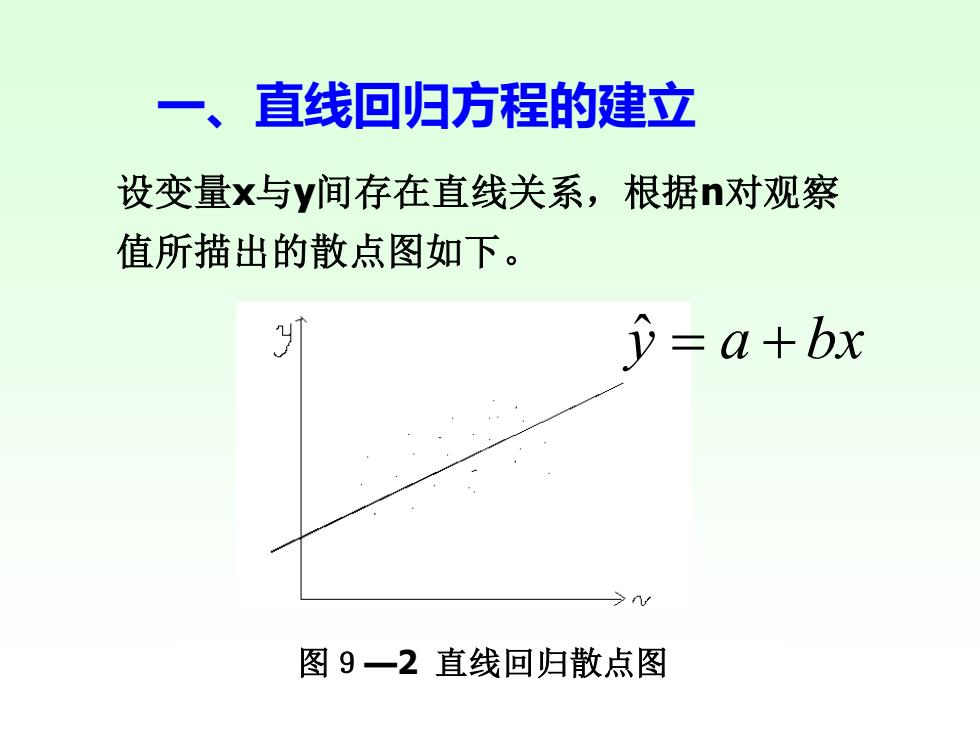
一 直线回归方程的建立 设变量x与y间存在直线关系,根据n对观察 值所描出的散点图如下。 =a+bx 图9一2直线回归散点图
一、直线回归方程的建立 设变量x与y间存在直线关系,根据n对观察 值所描出的散点图如下。 y ˆ = a + bx 图9—2 直线回归散点图

总体直线回归方程:y=a+x 实际观察值可表示为: y1=0+βx+e(i=1,2,.,n) e为随机误差,与o、B相互独立 ,且服从 N(0,σ2)。这就是直线回归的数学模型 根据样本实际观察值对α、β以及误差方差 σ作出估计,即建立样本回归方程并估计 出误差的大小
总体直线回归方程:y=α+βx 实际观察值可表示为: yi =α+βxi+i (i=1,2,.,n) i为随机误差,与α、β相互独立,且服从 N(0,2)。这就是直线回归的数学模型 根据样本实际观察值对α、β以及误差方差 2作出估计, 即建立样本回归方程并估计 出误差的大小