章 第九章回归与相关分析 课时 4 &9.1回归和相关分析概述 节 &9.2直线回归分析 &9.3直线相关分析 督酷 通过讲授,使学生了解回归与相关分析:弄清回归与相关的区别与联系。 掌握简单相关分析和一元直线回归分析的方法和意义。 教学 本章的重点是对直线回归方程的实际应用。 重点 直线回归方程拟合原理,直线回归分析各统计区间估计的计算与统计意义 教学 的分析。 难点 方法:通过绘图与统计原理结合,讲思路与推导结果,使学生理解以至会 灵活应用,而不讲授公式的完整推导过程,重在应用。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997 10.《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 《试验设计与分析》,袁志发主编,高等教育出版社,2000
1 章 第九章 回归与相关分析 课时 4 节 &9.1 回归和相关分析概述 &9.2 直线回归分析 &9.3 直线相关分析 教学 目的 通过讲授,使学生了解回归与相关分析;弄清回归与相关的区别与联系。 掌握简单相关分析和一元直线回归分析的方法和意义。 教学 重点 本章的重点是对直线回归方程的实际应用。 教学 难点 直线回归方程拟合原理,直线回归分析各统计区间估计的计算与统计意义 的分析。 方法:通过绘图与统计原理结合,讲思路与推导结果,使学生理解以至会 灵活应用,而不讲授公式的完整推导过程,重在应用。 相关素材(参考资料、指导学生阅读材料等): 列出主要参考文献 1. 《试验统计方法》,盖钧镒主编,中国农业出版社,2000。 2. 《试验设计与统计分析》,金益主编,中国农业出版社,2007。 3. 《SAS 统计分析教程》,唐燕琼主编,中国农业出版社,2006。 4. 《试验统计引论》,韩汉鹏主编,中国林业出版社,2006。 5. 《热带作物的试验设计与统计分析》,林德光著,华南热带农业大学,1985。 6. 《生物统计的数学原理》,林德光,辽宁人民出版社,1982。 7. 《试验设计与统计分析学习指导》,黄亚群主编,中国农业出版社,2008。 8. 《果树试验设计与统计》,刘权主编,中国农业出版社,1997。 9. 《肥料试验及统计分析》,陶勤南主编,中国农业出版社,1997。 10. 《食品试验设计与统计分析》,王钦德主编,中国农业出版社,2002。 《试验设计与分析》,袁志发主编,高等教育出版社,2000

教师授课思路、设问及讲解要点 一、引言 前面学的试验结果的统计方法,都是属于同一类数的测验,如作物的产量, 发病率等,这些都有是不同品种或不同处理对某一类变数的效应,但我们在生产 试验中,常会遇到二类变数以及两类以上变数间关系。例如,土、肥、种、水等 任何一个与产量的关系,新梢生长量与坐果率的关系,橡胶白粉病与越冬菌量的 关系:研究每亩穗数、每穗粒数和每亩产量的关系,就有穗数、粒数和产量三 个变数。本章介绍两个以上变数的统计分析方法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &9.1回归和相关分析概述 在农林科研中,同一现象中的若干变量往往存在着统计相关关系,它们虽互 相依存,但一般来说,其中一个并不能由其余几个完全确定。 一、变量间的关系分为两类: 函数关系:完全确定性的关系 一可用精确的数学式来表示: 统计关系:不存在完全确定性的关系一一不能用精确的数学式来表示。 统计相关关系有两种:因果关系,如种植因,作物产量是果:另一种是平等关 系,即两变量是互为因果或有共同的因,它们表现出一定程度的借同变异。如玉 米穗长和穗粗,大豆的每荚粒数和粒重,是偕同变量而不是谁决定谁。 程 统计关系这一类变量间的关系就是统计学中回归分析与相关分析所要讨论的 问题。 二、回归、相关分析的任务与类型 常用x、y来表示两个变量,(x,y)的各对观察值用(x,y),(x,y),(x,y) 表示。 在统计上,x和y变量的关系有两种理论模型:回归模型和相关模型。 在回归模型中,X是固定的(试验时预先确定的),没有误差或误差很小, 而Y则不仅随X的变化而变化,并且有随机误差,一般X叫自变数,Y叫因变数 回归分析目的:导出由x来预测或控制y的回归方程,即确定当自变量x为 某一值时依变量y将会在什么范围内变化。 在相关模型中,其x和y变量是平行变化关系,皆具有随机误差,因而不能 区别哪一个自变数,依变数,也不具有预测性质。 相关分析目的:确定两个变量在数量关系上的密切程度和性质。不能用一个 或多个变量去预测、控制另一个变量的变化。 回归分析的类型:一元回归分析(直线和曲线回归分析)为 多元线性回归分析和曲面回归分析)
2 教 学 过 程 教师授课思路、设问及讲解要点 一、引言 前面学的试验结果的统计方法,都是属于同一类数的测验,如作物的产量, 发病率等,这些都有是不同品种或不同处理对某一类变数的效应,但我们在生产 试验中,常会遇到二类变数以及两类以上变数间关系。例如,土、肥、种、水等 任何一个与产量的关系,新梢生长量与坐果率的关系,橡胶白粉病与越冬菌量的 关系;研究每亩穗数、每穗粒数和每亩产量的关系,就有穗数、粒数和产量三 个变数。本章介绍两个以上变数的统计分析方法。 二、教学内容正文(含讲课内容、提问设计、课堂练习等) &9.1 回归和相关分析概述 在农林科研中,同一现象中的若干变量往往存在着统计相关关系,它们虽互 相依存,但一般来说,其中一个并不能由其余几个完全确定。 一、变量间的关系分为两类: 函数关系:完全确定性的关系——可用精确的数学式来表示; 统计关系:不存在完全确定性的关系——不能用精确的数学式来表示。 统计相关关系有两种:因果关系,如种植因,作物产量是果;另一种是平等关 系,即两变量是互为因果或有共同的因,它们表现出一定程度的偕同变异。如玉 米穗长和穗粗,大豆的每荚粒数和粒重,是偕同变量而不是谁决定谁。 统计关系这一类变量间的关系就是统计学中回归分析与相关分析所要讨论的 问题。 二、回归、相关分析的任务与类型 常用 x、y 来表示两个变量,(x,y)的各对观察值用(x1,y1),(x2,y2),.,(xn,yn) 表示。 在统计上,x 和 y 变量的关系有两种理论模型:回归模型和相关模型。 在回归模型中,X 是固定的(试验时预先确定的),没有误差或误差很小 , 而 Y 则不仅随 X 的变化而变化,并且有随机误差,一般 X 叫自变数,Y 叫因变数。 回归分析目的:导出由 x 来预测或控制 y 的回归方程,即确定当自变量 x 为 某一值时依变量 y 将会在什么范围内变化。 在相关模型中,其 x 和 y 变量是平行变化关系,皆具有随机误差,因而不能 区别哪一个自变数,依变数,也不具有预测性质。 相关分析目的:确定两个变量在数量关系上的密切程度和性质。不能用一个 或多个变量去预测、控制另一个变量的变化。 回归分析的类型:一元回归分析(直线和曲线回归分析); 多元线性回归分析和曲面回归分析)
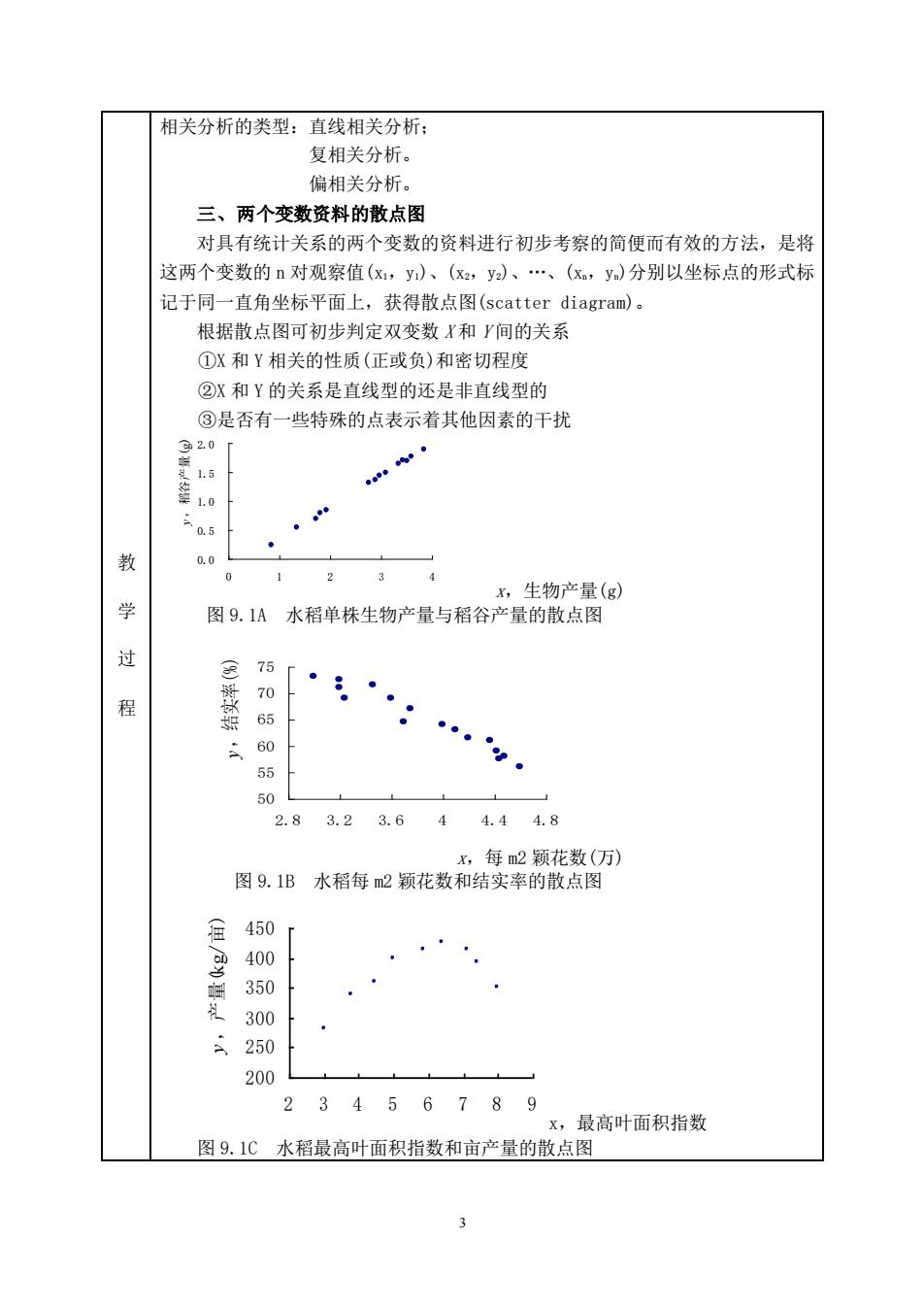
相关分析的类型:直线相关分析: 复相关分析。 偏相关分析。 三、两个变数资料的散点图 对具有统计关系的两个变数的资料进行初步考察的简便而有效的方法,是将 这两个变数的n对观察值(x,y)、(x,y)、·、(x,y)分别以坐标点的形式标 记于同一直角坐标平面上,获得散点图(scatter diagram))。 根据散点图可初步判定双变数X和y间的关系 ①X和Y相关的性质(正或负)和密切程度 ②X和Y的关系是直线型的还是非直线型的 ③是否有一些特殊的点表示着其他因素的干扰 320 0.5 . 教 0.0 0 2 3 4 x,生物产量(g) 图9.1A水稻单株生物产量与稻谷产量的散点图 75 ÷60 。 50 2.83.23.6 4 4.44.8 x,每2额花数(万) 图9.1B水稻每m2颖花数和结实率的散点图 450 400 350 300 250 200 2 3456789 x,最高叶面积指数 图9.1C水稻最高叶面积指数和亩产量的散点图
3 教 学 过 程 相关分析的类型:直线相关分析; 复相关分析。 偏相关分析。 三、两个变数资料的散点图 对具有统计关系的两个变数的资料进行初步考察的简便而有效的方法,是将 这两个变数的 n 对观察值(x1,y1)、(x2,y2)、.、(xn,yn)分别以坐标点的形式标 记于同一直角坐标平面上,获得散点图(scatter diagram)。 根据散点图可初步判定双变数 X 和 Y 间的关系 ①X 和 Y 相关的性质(正或负)和密切程度 ②X 和 Y 的关系是直线型的还是非直线型的 ③是否有一些特殊的点表示着其他因素的干扰 x,生物产量(g) 图 9.1A 水稻单株生物产量与稻谷产量的散点图 x,每 m2 颖花数(万) 图 9.1B 水稻每 m2 颖花数和结实率的散点图 x,最高叶面积指数 图 9.1C 水稻最高叶面积指数和亩产量的散点图 0.0 0.5 1.0 1.5 2.0 0 1 2 3 4 y,稻谷产量(g) 50 55 60 65 70 75 2.8 3.2 3.6 4 4.4 4.8 y ,结实率(%) 200 250 300 350 400 450 2 3 4 5 6 7 8 9 y ,产量(kg/亩)

&9.2直线回归分析 一、直线回归方程的建立 设变量x与y间存在直线关系,根据n对观察值所描出的散点图如下。 i=a+bx →X 图9一2直线回归散点图 教 总体直线回归方程:y=a+Bx 实际观察值可表示为: 学 y,=a+Bx+8(i=l,2,.,n) 8为随机误差,与a、B相互独立,且服从N(0,σ)。这就是直线回归的数学 过 模型 根据样本实际观察值对α、B以及误差方差。2作出估计,即建立样本回归 方程并估计出误差的大小。 设样本直线回归方程为:=a+br 总体直线回归方程: y=a+B x 其中a是a的估计值,称为回归截距 b是B的估计值,称为回归系数,表示自变量每改变一个单位数时,依变量 y平均改变的单位数(6>0时,增加:b<0时,减少) 回归方程的基本条件(性质): 性质1Q=∑0y-)2=最小 性质2∑y-)=0 性质3回归直线通过点(不,) Q=∑y-)2=∑[y-(a+bx)f 利用最小二乘法,即Q最小的方法求a与b的值。根据微积分学中求极值 原理,将Q对a与b求偏导数并令其等于0:
4 教 学 过 程 &9.2 直线回归分析 一、直线回归方程的建立 设变量 x 与 y 间存在直线关系,根据 n 对观察值所描出的散点图如下。 图9—2 直线回归散点图 总体直线回归方程:y=α+βx 实际观察值可表示为: yi =α+βxi+i (i=1,2,.,n) i为随机误差,与α、β相互独立,且服从 N(0, 2 )。这就是直线回归的数学 模型 根据样本实际观察值对α、β以及误差方差 2 作出估计, 即建立样本回归 方程并估计出误差的大小。 设样本直线回归方程为: y ˆ = a + bx 总体直线回归方程: y=α+βx 其中 a 是 的估计值,称为回归截距; b 是β的估计值,称为回归系数,表示自变量每改变一个单位数时, 依变量 y 平均改变的单位数(b>0 时,增加;b<0 时,减少) 回归方程的基本条件(性质): 性质1 最小 性质 2 (y − y ˆ) = 0 性质 3 回 归 直 线 通 过 点 = − = − + 2 2 ( ˆ ) ( ) i i i a bxi Q y y y 利用最小二乘法,即Q最小的方法求 a 与 b 的值。根据微积分学中求极值的 原理,将 Q 对 a 与 b 求偏导数并令其等于 0: y ˆ = a + bx = − = 2 Q (y y ˆ) (x, y)

.-2∑0y-a-bx)=0 aa ab =-2∑0y-a-bx)x=0 整理后可得: m+(∑xb=∑y (∑xa+(∑x)b=∑xy 上式叫做a与b的正规方程组。 解之可得: h-∑-∑x∑n ∑x2-(∑x)21n a=p-b标 简记为: 举 b2”-n ∑x2-(∑x)21n 学 a=-b饭 Σ(x-y-列=Σxy-Σx∑y/n称之为x与y的离均差乘积和,简称为乘积 和,记为SP,。 若记ss.=∑x2-(Ex)2/n,则 b=SP SS, a=-b a、b是a、B的最小二乘估计也是无偏估计。 例[9.1]一些夏季害虫盛发期的早迟和春季温度高低有关。江苏武进连续9年 测定3月下旬至4月中旬旬平均温度累积值(x,旬.度)和水稻一代三化螟胜发期 (y,以5月10日为0)的关系,得结果于表9.1。试计算其直线回归方程。 表9.1累积温和一代三化螟胜发期的关系 积累温(x)5.534.131.740.336.840.231.739.244.2 盛发期(y)12169273139-1 解: n=9 ∑x=333.7 元=37.0778 SS,=(n-10S2=144.6356
5 教 学 过 程 = − − − = = − − − = 2 ( ) 0 2 ( ) 0 i i i i i y a bx x b Q y a bx a Q 整理后可得: + = + = i i i i i i x a x b x y na x b y 2 ( ) ( ) ( ) 上式叫做 a 与 b 的正规方程组。 解之可得: a y bx x x n x y x y n b i i i i i i = − − − = ( ) / ( )( )/ 2 2 简记为: a y bx x x n xy x y n b = − − − = ( ) / ( )( )/ 2 2 (x − x)(y − y) = xy−x y / n 称之为 x 与 y 的离均差乘积和, 简称为乘积 和,记为 SPxy 。 若记 ssx=∑x 2 -(∑x) 2/n,则 a y bx b SPxy SSx = − = / a、b 是α、β的最小二乘估计也是无偏估计。 例[9.1]一些夏季害虫盛发期的早迟和春季温度高低有关。江苏武进连续 9 年 测定 3 月下旬至 4 月中旬旬平均温度累积值(x,旬.度)和水稻一代三化螟胜发期 (y,以 5 月 10 日为 0)的关系,得结果于表 9.1。试计算其直线回归方程。 表 9.1 累积温和一代三化螟胜发期的关系 积累温(x) 35.5 34.1 31.7 40.3 36.8 40.2 31.7 39.2 44.2 盛发期(y) 12 16 9 2 7 3 13 9 -1 解: ( 1) 144.6356 333.7 37.0778 9 2 = − = = = = SSx Sx n x x n

∑y=70 =7.7778 SS,=(n-1)S2=249.5556 SP=Σ-∑∑.-159044 因而有:6=SP -1.0996天(旬·度】 Ss. a=-b=48.5485(天) 回归方程有:少=48.5485-1.0996y 或简化为:=48.5-1.1x 上述方程中回归系数和回归截距的意义为: 当3月下旬至4月中旬的积温(x)海提高1旬度时,一代三化螟的盛发期平均 将提早1.1天:若积温为0,则一代三化螟的盛发期将在6月27一28日(x=0时, =48.5:因y是以5月10日为0,故48.5为6月27-28日)。 由于x变数的实测区间为31.7,44.2引,当x44.2时,y的变化是 教 否还符合=48.5-L1x的规律,观察数据中未曾得到任何信息。所以,在应用 =48.5-11x于预测时,需限定x的区间为31.7,442小:如要在x44.2 的区间外延,则必须有新的依据。 二、直线回归的显著性检验 回归关系的假设测验: 对于样本的回归方程,必须测定其来自无直线回归关系总体的概率大小。只 有当这种概率小于0.05或0.01时,我们才能冒较小的危险确认其所代表的总体 存在着直线回归关系。这就是回归关系的假设测验。 回归关系的假设测验有两种方法:t测验或下测验 1、回归系数显著性检哈一 一t检验 对直线回归系数b的假设检验为: H0:B=0:HAB≠0。 在H0成立的条件下,回归系数b服从t分布 1=b/S。y=n-2.(9-8) 其中 ,为回归系数标准误 SS [例9.2】试测验例9.1资料回归关系的显著性。 己算得F-1.0996,SS=144.6356,sw=3.266, 故有: 3.266 “4=0.2716 6
6 教 学 过 程 1 249 5556 70 7 7778 2 ( ) . . = − = = = SSy Sy n y y = − = −159.0444 n x y SP xy y x y x a y bx SP b ss x ˆ 48.5 1.1 ˆ 48.5485 1.0996 48.5485( : 1.0996[ /( ] = − = − = − = = = − • 或简化为: 回归方程有: 天) 因而有 天 旬 度) 上述方程中回归系数和回归截距的意义为: 当 3 月下旬至 4 月中旬的积温(x)每提高 1 旬·度时,一代三化螟的盛发期平均 将提早 1.1 天;若积温为 0,则一代三化螟的盛发期将在 6 月 27—28 日(x=0 时, =48.5;因 y 是以 5 月 10 日为 0,故 48.5 为 6 月 27—28 日)。 由于 x 变数的实测区间为[31.7,44.2],当 x<31.7 或>44.2 时,y 的变化是 否还符合=48.5-1.1x 的规律,观察数据中未曾得到任何信息。所以,在应用 =48.5-1.1x 于预测时,需限定 x 的区间为[31.7,44.2];如要在 x<31.7 或>44.2 的区间外延,则必须有新的依据。 二、直线回归的显著性检验 回归关系的假设测验: 对于样本的回归方程,必须测定其来自无直线回归关系总体的概率大小。只 有当这种概率小于 0.05 或 0.01 时,我们才能冒较小的危险确认其所代表的总体 存在着直线回归关系。这就是回归关系的假设测验 。 回归关系的假设测验有两种方法:t 测验或 F 测验 1、回归系数显著性检验──t 检验 对直线回归系数 b 的假设检验为: HO :β=0;HA β≠0。 在 HO 成立的条件下,回归系数 b 服从 t 分布。 t = b / S df = n − 2.(9−8) b 其中 x y x b SS S S / = ,为回归系数标准误。 [例 9.2] 试测验例 9.1 资料回归关系的显著性。 已算得 b=-1.0996,SSx=144.6356,sy/x=3.266, 故有: 0.2716 144.6356 3.266 = = b s

1=-1096-0.-405 0.2715 查附表4,tns.=2.36,tm.=3.50。 |t=4.05>taL=3.50,应否定l:B=0,接受H:≠0 结论:认为积温和一代三化螟盛发期是有真实直线回归关系的。 或者说此:-1.0996是极显著的。 2.回归关系显著性检验—F检验 直线回归的变异来源 不9=a+bx 0y- 图9-4-)的分解图 y的总变异(y-)由y与x间存在直线关系所引起的变异(心-》 程 与偏差(y-)两部分构成,即y-卫=(y-)+(-) 将上式两端平方,求和,得: ∑y-)=∑【y-)+(-) -∑y-+2∑y-)+∑5-) 因为=a+br=+b(x-x),-=b(x-x) 则∑y-少-)=0 所以∑y-)2=∑心-)2+∑0y-)2 上式中: Dfa=1SS,=∑y-)2 回归平方和简记作,它是由的不同而引起的。 df 10=ΣG-jy=SP SS. 离归平方和:2=∑Uy-=SS,-SS期Dfw=m-2
7 教 学 过 程 4.05 0.2715 1.0996 0 = − − − t = 查附表 4,t0.05,7=2.36,t0.01,7=3.50。 |t|=4.05>t0.01,7=3.50,应否定 H0:β=0,接受 HA:≠0 结论:认为积温和一代三化螟盛发期是有真实直线回归关系的。 或者说此 b=-1.0996 是极显著的。 2.回归关系显著性检验──F 检验 ˆ ( ˆ 0 ˆ ( ˆ ( ˆ 2 ˆ ( ˆ ˆ ( ˆ) ˆ , : ˆ ˆ ˆ ˆ 2 2 2 2 − − = = + = + − − = − = − + − − + − − = − + − − − = − + − − − 则 ( ) ) 因为 ), ) ( ) ( ) ) ( ) ( ) ( ) 将上式两端平方 求和,得 与偏差( )两部分构成,即 ( )( ) 的总变异( )由 与 间存在直线关系所引起的变异( ) y y y y y a bx y b x x y y b x x y y y y y y y y y y y y y y y y y y y y y y y y y y x y y − = − + − 2 2 2 所以 (y y) (y ˆ y) (y y ˆ) 上式中: = − ( )2 SS y y y 回归平方和简记作U,它是由x的不同而引起的。 df 回归=1 SSx SP U y y 2 2 ( ) = ( ˆ − ) = 离归平方和: Q = y − y = SSy − SS回归 2 ( ˆ) Df离回归=n-2 图9-4 ( y − y) 的分解图 直线回归的变异来源 Df总=1

[例9.3]试用F测验法检测例9.1资料回归关系的显著性 己算得SS.=144.6356 SSy=249.5556 SP=-159.044 回归平方和U=SP_-1590444 144.6356 离回归平方和: SS, 2=SS,-SSa自=249.5556-174.8886-74.6670 表9.3例9.1资料回归关系的方差分析 变异来源F 回 归1174.8886174.888616.40*12.25 离回归774.667010.6667 总变异8249.5556 结论:表明积温和一代三化螟盛发期是有真实直线回归关系的,即B≠0(准 确地说,在B=0的总体中获得现有回归样本的概率小于0.01)。 统计学己证明,在直线回归分析中F检验与t检验法是等价的,可任选一种 进行检验。 学 特别要指出的是:利用直线回归方程进行预测或控制,一般只能内插,不要 轻易外延。 程
8 教 学 过 程 [例 9.3] 试用 F 测验法检测例 9.1 资料回归关系的显著性。 已算得 SSX=144.6356 SSy=249.5556 SP=-159.044 解: 回归平方和 离回归平方和: Q = SSy − SS回归 = 249.5556 −174.8886 = 74.6670 表 9.3 例 9.1 资料回归关系的方差分析 变异来源 DF SS MS F F0.01 回 归 1 174.8886 174.8886 16.40** 12.25 离 回 归 7 74.6670 10.6667 总 变 异 8 249.5556 结论:表明积温和一代三化螟盛发期是有真实直线回归关系的,即β≠0(准 确地说,在β=0 的总体中获得现有回归样本的概率小于 0.01)。 统计学已证明,在直线回归分析中 F 检验与 t 检验法是等价的,可任选一种 进行检验。 特别要指出的是:利用直线回归方程进行预测或控制,一般只能内插,不要 轻易外延。 144.6356 ( 159.0444) 2 − = = SSx SP U 2 ( )

&9.3直线相关分析 ,决定系数和相关系数 ∑0y-)2=∑-)2+∑0y-) y与x直线回归效果的好坏取决于回归平Σ(-)2与离回归平方和 Σy-的大小,或者说取决于回归平方和在y的总平方和中所占比例的大小 0-列/∑y-列叫做x对y的决Σ0-或定系数记为已,即 产.0-y 决定系数n的大小表示了回归方程的可靠程度,显然有0≤2≤1。因为 2= ∑-2 SPi SPSP 0-のs85s,s8.ss bx=SPxy/SSx是x为自变量、y为依变量时的回归系数。 决定系数rP等于y对x的回归系数bx与x对y的回归系数by的乘积 r2=byxbxy 过 决定系数P表示了互为因果关系的相关变量x与y间直线关系的程度。但决 定系数介于0与1之间,不能反映x与y直线关系的性质一是同向增诚或异向增 减。 相关系数(coefficient of correlation),记为r,即 r=- SP SSSS, 显然相关系数介于1与+1之间, 即1≤≤1。 若仁1,为完全负相关:=+1,为完全正相关。 在农业研究中,完全相关的情况很罕见,多数相关系数是大于-1,小于+1的 二、相关系数的显著性检验 相关系数r是样本相关系数,它是双变量正态总体中的总体相关系数p的估 计值。 无效假设、备择假设为: H:p=0: H:p≠0。 可采用上检验法、F检验法及查表法对相关系数r的显著性进行检验。 查表法:先根据自由度n-2查临界r值(附表8),得nos,ao1 9
9 教 学 过 程 &9.3 直线相关分析 一、决定系数和相关系数 y 与 x 直线回归效果的好坏取决于回归平方和 与离回归平方和 − 2 (y y ˆ) 的大小,或者说取决于回归平方和在 y 的总平方和中所占比例的大小。 叫做 x 对 y 的决 − 2 (y y ˆ) 定系数记为 r 2,即 − − = 2 2 2 ( ) ( ˆ ) y y y y r 决定系数 r2 的大小表示了回归方程的可靠程度,显然有 0≤r2≤1。因为 byx =SPxy/SSx 是 x 为自变量、y 为依变量时的回归系数。 决定系数 r 2 等于 y 对 x 的回归系数 byx 与 x 对 y 的回归系数 bxy的乘积 r 2=byxbxy 。 决定系数 r 2 表示了互为因果关系的相关变量 x 与 y 间直线关系的程度。但决 定系数介于 0 与 1 之间,不能反映 x 与 y 直线关系的性质──是同向增减或异向增 减。 相关系数(coefficient of correlation),记为 r,即 x y xy SS SS SP r = 显然相关系数介于-1 与+1 之间, 即 -1≤r≤1。 若 r=-1,为完全负相关; r=+1,为完全正相关。 在农业研究中,完全相关的情况很罕见,多数相关系数是大于-1,小于+1 的。 二、相关系数的显著性检验 相关系数 r 是样本相关系数,它是双变量正态总体中的总体相关系数ρ的估 计值。 无效假设、备择假设为: HO:ρ=0 ; HA:ρ≠0。 可采用 t 检验法、F 检验法及查表法对相关系数 r 的显著性进行检验。 查表法: 先根据自由度 n-2 查临界 r 值(附表 8),得 0.05 0.01 r ,r − = − + − 2 2 2 (y y) (y ˆ y) (y y ˆ) − 2 ( y ˆ y) − − 2 2 (y ˆ y) / (y y) y xy x xy x y xy SS SP SS SP SS SS SP y y y y r = = − − = ( ) . ( ˆ ) 2 2 2 2

若r0.05,则相关系数r不显著: 若na1≤r<os,0.01<P<0.05,则相关系数r显著,标记“*”: 若r≥01,P≤0.01,则相关系数r极显著,标记“*”。 [例9.4]试计算例9.1资料3月下旬至4月中旬积温和一代三化螟盛发期 的相关系数和决定系数。 已算得该资料的SS=144.6356,5S=249.5556,SP-159.0444,故 -159.0444 5y14.6356×2419.556-0837 r= r2=(-0.83712-0.7008 r=-0.8371表明:一代三化螟盛发期与3月下旬至4月中旬的积温成负相关, 即积温愈高,一代三化螟盛发期愈早。 r=0.7008表明:在一代三化螟盛发期的变异中有70.08%是由3月下旬至4 月中旬的积温不同造成的。 举 三、直线回归与直线相关的联系 r=1babo 研究对象都是呈直线关系的相关变量。 过 直线回归分析将二个相关变量区分为自变量与依变量,侧重于寻求它们之间的联 系形式一建立有线同归方程。 直线相关分析不区分自变量于依变量,侧重于揭示它们之间联系程度与性质 计算出相关系数。 两种分析的显著性检验都是解决y与x是否存在直线关系,因而二者的检验 是等价的。 可用相关系数显著性检验代替直线回归关系显著性检验,即可先计算相关系 数r并对其进行检验,显著后再建立直线回归方程。 四、应用直线回归与相关的注意事项 1、要考虑到客观实际情况。 2、要考虑到回归系数、相关系数的适用范围 3、必须严格控制被研究的两个变量以外的各个变量的变动范围。 4、两个样本的容量一般不应小于5。 5、正确理解“相关不显著”和“回归不显著”。 三、总结与巩固 1.小结 回归分析与相关分析概述,回归与相关的区别与联系,直线回归与曲线回归, 元直线与多元线性回归:简单相关相关系数的定义、计算及其相关系数显著性
10 教 学 过 程 若|r|< 0.05 r ,P>0.05,则相关系数 r 不显著; 若 0.01 r ≤|r|< 0.05 r ,0.01<P<0.05,则相关系数 r 显著,标记“*”; 若|r|≥ 0.01 r ,P≤0.01, 则相关系数 r 极显著,标记“**”。 [例 9.4] 试计算例 9.1 资料 3 月下旬至 4 月中旬积温和一代三化螟盛发期 的相关系数和决定系数。 已算得该资料的 SSx=144.6356,SSy=249.5556,SP=-159.0444,故 0.837 144.6356 249.5556 159.0444 = − − = = y ss x ss sp r . = − = 0.7008 2 ( 0.8371) 2 r r=-0.8371 表明:一代三化螟盛发期与 3 月下旬至 4 月中旬的积温成负相关, 即积温愈高,一代三化螟盛发期愈早。 r 2 =0.7008 表明:在一代三化螟盛发期的变异中有 70.08%是由 3 月下旬至 4 月中旬的积温不同造成的。 三、直线回归与直线相关的联系 byxbxy r = 研究对象都是呈直线关系的相关变量。 直线回归分析将二个相关变量区分为自变量与依变量,侧重于寻求它们之间的联 系形式──建立直线回归方程; 直线相关分析不区分自变量于依变量,侧重于揭示它们之间联系程度与性质 ──计算出相关系数。 两种分析的显著性检验都是解决 y 与 x 是否存在直线关系,因而二者的检验 是等价的。 可用相关系数显著性检验代替直线回归关系显著性检验,即可先计算相关系 数 r 并对其进行检验,显著后再建立直线回归方程。 四、应用直线回归与相关的注意事项 1、要考虑到客观实际情况。 2、要考虑到回归系数、相关系数的适用范围。 3、必须严格控制被研究的两个变量以外的各个变量的变动范围。 4、两个样本的容量一般不应小于 5。 5、正确理解“相关不显著”和“回归不显著”。 三、总结与巩固 1.小结 回归分析与相关分析概述,回归与相关的区别与联系,直线回归与曲线回归, 一元直线与多元线性回归;简单相关相关系数的定义、计算及其相关系数显著性