
§2概率的定义及其确定方法 研究随机现象不仅关心试验中会出现哪些事件,或者某事 件发生的可能性大不大,即只有一个定性的描述是不够的,准确了 解事件发生的可能性即概率的大小,对人们的生活有重要意义 例如,了解发生意外人身事故的可能性大小 确定保险金额! 了解来商场购物的顾客人数的各种可能性 大小,合理配置服务人员. 了解每年最大洪水超警 戒线可能性大小,合理确定 堤坝高度。 更重要的是对事件出现的可能性的大小有 个定量的描述,这就需要有一个度量事件发生可能性大小的数量指 标,事件的概率就是事件发生的可能性大小的一个数值度量
事件的概率就是事件发生的可能性大小的一个数值度量. 更重要的是对事件出现的可能性的大小有一 个定量的描述. §2 概率的定义及其确定方法 研究随机现象不仅关心试验中会出现哪些事件,或者某事 件发生的可能性大不大, 准确了 解事件发生的可能性即概率的大小,对人们的生活有重要意义. 即只有一个定性的描述是不够的, 这就需要有一个度量事件发生可能性大小的数量指 标, 了解来商场购物的顾客人数的各种可能性 大小,合理配置服务人员. 了解每年最大洪水超警 戒线可能性大小,合理确定 堤坝高度. 例如,了解发生意外人身事故的可能性大小, 确定保险金额
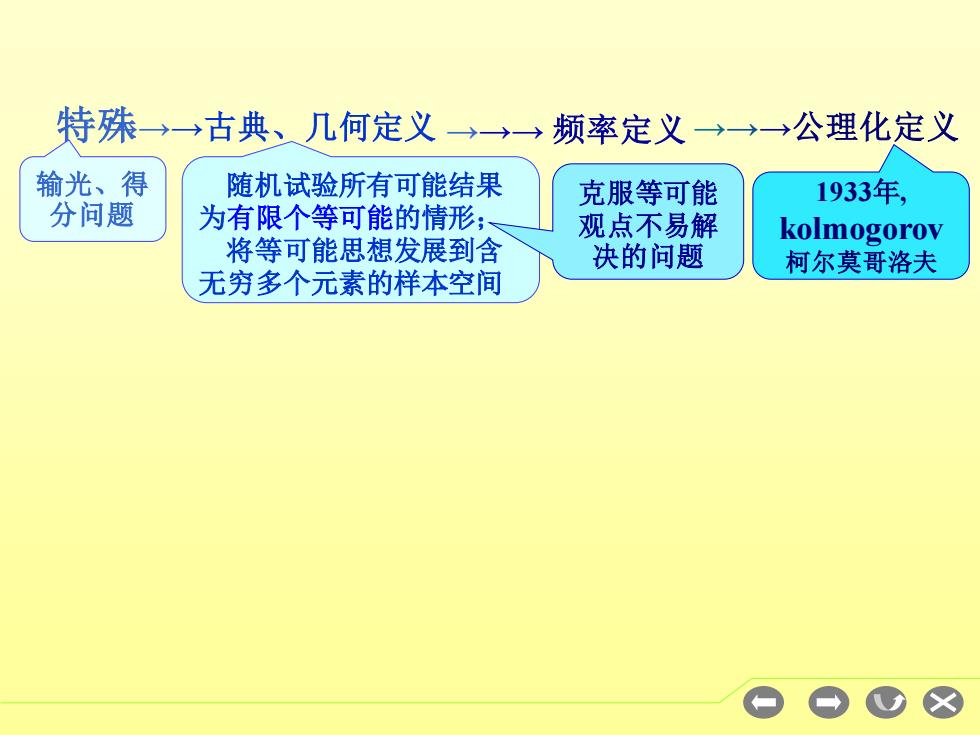
特殊→→古典、几何定义 ,→→→频率定义→→→公理化定义 输光、得 随机试验所有可能结果 克服等可能 1933年, 分问题 为有限个等可能的情形, 观点不易解 kolmogorov 将等可能思想发展到含 决的问题 柯尔莫哥洛夫 无穷多个元素的样本空间
特殊 1933年, kolmogorov 柯尔莫哥洛夫 随机试验所有可能结果 为有限个等可能的情形; 将等可能思想发展到含 无穷多个元素的样本空间 输光、得 分问题 克服等可能 观点不易解 决的问题 →→→古典、几何定义 →→→ 频率定义 →→→公理化定义

1.2.1概率的公理化定义 定义2设2是一个样本空间,F为的某些子集组成的一个事件域, 若对于2中的每一个事件A∈F,定义在F上的一个实值函数P(A) 满足: 非负性 一(1)若事件A∈F,则P(A)≥0, 正则性 (2) P(2)=1, 可列 一(3)若事件A1,A2,…,A,…两两互不相容,则有 可加性 P(A1+A2+…+An+=P(A1)+P(A2)+…P(An)+ 称P(4)为事件4的概率, 称三元素(①,EP)为概率空间 数学上所说的“公理”,就是一些不加证明而公认的前提, 然后以此为基础,推演出所讨论对象的进一步的内容. 在学习几何和代数时,我们已经知道公理是数学体系的基础. 柯尔莫哥洛夫提出的公理为数很少且极为简单,但在此基础 上建立起了概率论的宏伟大厦. 柯尔莫哥格夫,A.H. 由概率的三条公理,我们可推导出概率的若干重要性质.它们 在计算概率时很有用,尤其是加法公式
但在此基础 上建立起了概率论的宏伟大厦. 它们 在计算概率时很有用,尤其是加法公式. 若对于 中的每一个事件AF,定义在F上的一个实值函数P(A) 满足: (2) P( )= 1 , (3) 若事件A1 , A2 , … , An ,… 两两互不相容,则有 P(A1 + A2 ++ An +) = P(A1 ) + P(A2 ) +P(An ) + (1) 若事件A F,则 P(A) 0 , 设是一个样本空间, F 为的某些子集组成的一个事件域, 1.2.1 概率的公理化定义 定义2 称P(A)为事件A的概率, 在学习几何和代数时,我们已经知道公理是数学体系的基础. 柯尔莫哥洛夫提出的公理为数很少且极为简单, 非负性 正则性 可列 可加性 由概率的三条公理,我们可推导出概率的若干重要性质. 数学上所说的“公理”,就是一些不加证明而公认的前提, 然后以此为基础,推演出所讨论对象的进一步的内容. 称三元素(,F, P )为概率空间

1.2.2排列与组合公式 这里我们先简要复习一下计算古典概率所要用到的两个基本计 数原理.它们不但可以直接解决不少具体问题,同时也是推导常用 排列组合公式的基础. (1)加法原理设完成一件事有种方式,第一种方式有n,种方法, 第二种方式有,种方法,…;第m种方式有n,m种方法,无论通 过哪种方法都可以完成这件事, 则完成这件事总共有n1+2+.+nm种方法. 例如,甲城到乙城有3条旅游路线,乙城到丙城有2条旅游路线, 则从甲城经乙城到丙城就有3×2=6条旅游路线, (2)乘法原理设完成一件事有个步骤,第一个步骤有n,种方法, 第二个步骤有2种方法,·;第个步骤有nm种方法, 则完成这件事共有m×2×…×nm种不同的方法, 例如,甲城到乙城去旅游有3类交通工具:汽车、火车和飞机, 而汽车有5个班次,火车有5个班次,飞机有2个班次,则从甲城到 乙城去旅游就有5+3+2=10个班次可供选择
则从甲城到 乙城去旅游就有5+3+2= 10 个班次可供选择. 无论通 过哪种方法都可以完成这件事, 1.2.2 排列与组合公式 这里我们先简要复习一下计算古典概率所要用到的两个基本计 数原理. (1) 加法原理 设完成一件事有m种方式,第一种方式有n1种方法, 第二种方式有n2种方法, … ; 第m种方式有nm种方法, 则完成这件事总共有n1 + n2 + … + nm 种方法 . 例如,甲城到乙城有3条旅游路线,乙城到丙城有2条旅游路线, 则从甲城经乙城到丙城就有32= 6 条旅游路线. 则完成这件事共有 n1 n2 nm 种不同的方法. (2)乘法原理 设完成一件事有m个步骤,第一个步骤有n1种方法, 第二个步骤有n2种方法, … ;第m个步骤有nm种方法, 它们不但可以直接解决不少具体问题,同时也是推导常用 排列组合公式的基础. 例如,甲城到乙城去旅游有3类交通工具:汽车、火车和飞机, 而汽车有5个班次,火车有5个班次,飞机有2个班次

排列、组合的定义及其计算公式 (1)排列从n个不同元素取r个(r≤)排成一列(考虑先后顺序), 称其为一个排列.由乘法原理,此种排列的总数为 p%=(n-1)(n-2)(n-k+1)= l (n-k)川 r=n时称全排列.显然 P"=pn=(n-1(n-2)…2.1=l (2)重复排列从个不同元素中每次取1个,放回后再取下一个, 如此连续取r次(可以大于)所得的排列称为重复排列,此种重复 排列的总数为nr
此种重复 排列的总数为 (1)排列 从n个不同元素取r 个(r n)排成一列(考虑先后顺序), 称其为一个排列. P p n(n )(n ) n! n n n = = −1 − 2 21 = 排列、组合的定义及其计算公式 ( )! ! ( )( ) ( ) n k n p n n n n k k n − = −1 − 2 − +1 = (2)重复排列 从n个不同元素中每次取1个,放回后再取下一个, r = n时称全排列. 由乘法原理,此种排列的总数为 显然 如此连续取r 次(r可以大于n)所得的排列称为重复排列, nr

(3)组合 从个不同元素任取k个(k≤)并成一组(不考虑先后顺序), 称其为一个组合。此种组合的总数记为)或C你 由乘法原理, 组合总数为 C= n! k=(n-K):k (2)重复组合从个不同元素中每次取1个,放回后再取下一个, 如此连续取r次(r可以大于)所得的组合称为重复组合,此种重复 组合的总数为C+-1 使用排列组合的概念与公式时,应注意其对有序与无序、 重复与不重复的要求
此种重复 组合的总数为 由乘法原理, 组合总数为 此种组合的总数记为 或 , ( )! ! ! ! n k k n k P C k k n n − = = (3)组合 k Cn k n 从n个不同元素任取k 个(k n)并成一组(不考虑先后顺序), 称其为一个组合. (2)重复组合 从n个不同元素中每次取1个,放回后再取下一个, 如此连续取r 次(r可以大于n)所得的组合称为重复组合, n+r−1 Cr 使用排列组合的概念与公式时,应注意其对有序与无序、 重复与不重复的要求

1.2.3确定概率的频率方法 定义1如果在n次重复试验中事件A发生了n(A)次,则称n(A)为 事件A发生的频数,称比值“为事件A在n次试验中出现的频率, 记为fn(A),即 A发生的 f(A)=n(A) 频繁程度 稳定性? 基本性质 事件的统计规律性 参见P14的 (1)0≤f(A)≤1; 非负性 三个例子 (2)fn(2)=1; 正规性 (3)设A1,A2,…,Ak两两互不相容的事件,则 有限 可加性 fn(A1+A2++Ak)=fn(A)+fn(A2)+…+fn(Ak) 即满足公理化定义
则称n(A)为 事件A发生的频数, 称比值 为事件A在n次试验中出现的频率, 定义1 如果在n次重复试验中事件A发生了n(A)次, n n(A) 记为 f n (A), n n A fn A ( ) ( ) = 即 A 发生的 频繁程度 基本性质 (1) 0 f (A) 1; n (3) 设A1, A2,…, Ak 两两互不相容的事件,则 (2) ( ) = 1; n f ( ) ( ) ( ) ( ) n 1 2 k n 1 n 2 n Ak f A + A ++ A = f A + f A ++ f 稳定性 事件的统计规律性 ? 非负性 正规性 有限 可加性 1.2.3 确定概率的频率方法 参见P14 的 三个例子 即满足公理化定义

用频率确定概率是一种常用的方法.其基本思想是: (1)与考察事件A有关的随机现象可大量重复进行: (2)人们长期实践表明:随着实验重复次数的增加, 频率fn(4A)会稳定在某一常数a附近,称常数a为频率的稳定值; 这个频率的稳定值就是我们所求的概率; (3)频率方法的缺点一一现实中,人们无法把一个实验无 限次地重复下去,因此要精确地得到频率的稳定值是困难的。 但频率方法提供了概率的一个可供想象的具体值,并且当 实验重复次数较大时,可用频率给出概率的一个近似值.故 称频率为概率的估计值.这正是频率方法最有价值的地方
并且当 实验重复次数n 较大时,可用频率给出概率的一个近似值. 用频率确定概率是一种常用的方法. 其基本思想是: (1) 与考察事件A 有关的随机现象可大量重复进行; (2) 人们长期实践表明: 随着实验重复次数n 的增加, 频率 fn(A)会稳定在某一常数a附近,称常数a为频率的稳定值; 这个频率的稳定值就是我们所求的概率; (3) 频率方法的缺点 ——现实中,人们无法把一个实验无 限次地重复下去,因此要精确地得到频率的稳定值是困难的. 但频率方法提供了概率的一个可供想象的具体值, 故 称频率为概率的估计值. 这正是频率方法最有价值的地方

1.2.4确定概率的古典方法 古典方法的基本思想: (1)样本空间2只有有限多个样本点,即2={w1,02,…,⊙n}; (2)每个样本点发生的可能性相等,一 等可能性 设事件A由k个样本点组成,即A={D,①2,,①i}, 由可加性知A的概率为: P(A)=上=A包含的样本点数 n2中的样本点总数 称此概率为古典概率.这种确定概率的方法称为古典方法, 这样就把求概率问题转化为计数问题
1.2.4 确定概率的古典方法 古典方法的基本思想: (1) 样本空间 只有有限多个样本点, (2) 每个样本点发生的可能性相等, 即 ={1 ,2 , ,n }; 等可能性 这样就把求概率问题转化为计数问题 . 设事件 A由 k个样本点组成,即 由可加性知A的概率为: { , , , }, A= i 1 i 2 i k ( ) ( ) ( ) P i 1 + P i 2 + + P ik n k = A 包含的样本点数 中的样本点总数 中的样本点总数 包含的样本点数 A n k P(A) = = 称此概率为古典概率. 这种确定概率的方法称为古典方法

例1(P14例9)同时掷两枚均匀硬币,分别求事件A={两枚都出现正面}, B={一枚出现反面}和C={两枚都出现反面}的概率, 解 同时掷两枚硬币有4个等可能的结果,即样本空间为 2={(正,正),(正,反),(反,正),(反,反)古典概型 又事件A,B,C分别包含1个、2个和1个样本点, P(A=49 P(C)=. 列举法 排列组合是计算古典概率的重要工具
同时掷两枚均匀硬币, 分别求事件A={两枚都出现正面}, B={一枚出现反面} 和 C={两枚都出现反面}的概率. 解 同时掷两枚硬币有4个等可能的结果,即样本空间为 例1(P14 例9) ={(正,正), (正,反), (反,正), (反,反)} 4个等可能 古典概型 又事件A, B, C 分别包含1个、2个和1个样本点, ; 4 1 P(A) = ; 2 1 4 2 P(B) = = . 4 1 P(C) = 排列组合是计算古典概率的重要工具 列 举 法