
§11 随机事件和样本空间 我们在引言中已经介绍了了随机试验,现在进 一步明确他的含义。一个试验如果满足下述条 件: 。(1) 试验可以在相同的情形下重复进行; 9(2) 试验的所有可能结果是明确可知道的, 并且不止一个: 。(3) 每次试验总是恰好出现这些可能结果 中的一个,但在一次试验之前却不能确定出现 哪一个结果;
§1.1 随机事件和样本空间 我们在引言中已经介绍了了随机试验,现在进 一步明确他的含义。一个试验如果满足下述条 件: (1) 试验可以在相同的情形下重复进行; (2) 试验的所有可能结果是明确可知道的, 并且不止一个; (3) 每次试验总是恰好出现这些可能结果 中的一个,但在一次试验之前却不能确定出现 哪一个结果;

就称这样的试验是一个随机试验,为方便起见,也称为试验。 随机试验的,每一格可能结果,称为基本事件。因为随机试验 的所有可能结果是明确的,从而所有的基本事件也是明确的, 他们的全体,称作样本空间,通常用字母表示,常用表示。 例1.1在前述试验Ⅱ中,令 o1={取得白球},o2={取得黑球 则 2={o1,02} 例1.2 个盒子中有十个完全相同的球分别标以号码1, 2,…,10,从中任取一球,令 i={取得球的标号为i} 则 2={1,2,.,10}
就称这样的试验是一个随机试验,为方便起见,也称为试验。 随机试验的,每一格可能结果,称为基本事件。因为随机试验 的所有可能结果是明确的,从而所有的基本事件也是明确的, 他们的全体,称作样本空间,通常用字母表示,常用表示。 例1.1 在前述试验Ⅱ中,令 1={取得白球}, 2={取得黑球} 则 ={ 1, 2} 例1.2 一个盒子中有十个完全相同的球分别标以号码1, 2,…,10,从中任取一球,令 i={取得球的标号为i} 则 ={1,2,…,10}

例1.1讨论某电话交换台在单位时间内收到的呼唤次数,令 i={收到的呼唤次数为i} 例1.2测量某地水温,令 t={测得的水温为t℃) 则 2=[0,100] 在随机试验中,有时关心的是带有某些特征的基本事件是否发生。 如在例1.2中,我们可以研究 A={球的标号=6} B={球的标号是偶数) C={球的标号小≤5} 这些结果是否发生?其中A是一个基本事件,而B与C则有多个基 本事件所组成,相对于基本事件,就称它们是复杂事件,无论是基 本事件还是复杂事件
例1.1 讨论某电话交换台在单位时间内收到的呼唤次数,令 i={收到的呼唤次数为 i } 例1.2 测量某地水温,令 t={测得的水温为 t℃} 则 =[0,100] 在随机试验中,有时关心的是带有某些特征的基本事件是否发生。 如在例 1.2 中,我们可以研究 A={球的标号=6} B={球的标号是偶数} C={ 球的标号小≤5 } 这些结果是否发生?其中 A 是一个基本事件,而 B 与 C 则有多个基 本事件所组成,相对于基本事件,就称它们是复杂事件,无论是基 本事件还是复杂事件

它们的试验中发生与否,都带有随机性,所以都叫作随机事件或简称为 事件。习惯上人们常用大写字母A,B,C等表示事件。在试验中,如果 出现A中所包含的某一个基本事件o,则称作A发生,并记作:O∈A. 我们已经知道样本空间2包含了全体基本事件,而随机事件不过是 某些特征的基本事件所组成,所以从集合论的观点来看,一个随机事件 不过是样本空间2的一格子集而已。如在例1.2中,2={1,2,…10}, 显然,前述的随机事件A,B,C都是2的子集,它们可以简单的表示为 A={6},B={2,4,6,8,10},C={1,2,3,4,5}。 又因为Ω是所有基本事件所组成,因而在任一次试验中,必然要出 现重的某一基本事件0,即0∈2。也就是在试验中, 2 必然会发 生,所以今后又2来代表一次必然事件。 相应地,空集②可以看做是o∈②,也就是说⑦永远不可能发生,所以 ☑是不可能事件。必然事件和不可能事件的发生与否,已经失去了“不 确定性”,因而本质上它们不是随机事件。但是为了方便起见,我们 还是把它们看作随机事件,稍后我们会理解,它们不过是随机事件的 两个极端情形而已
它们的试验中发生与否,都带有随机性,所以都叫作随机事件或简称为 事件。习惯上人们常用大写字母 A,B,C 等表示事件。在试验中,如果 出现 A 中所包含的某一个基本事件 ,则称作 A 发生,并记作: A. 我们已经知道样本空间 包含了全体基本事件,而随机事件不过是 某些特征的基本事件所组成,所以从集合论的观点来看,一个随机事件 不过是样本空间的一格子集而已。如在例 1.2 中, ={1,2,…10}, 显然,前述的随机事件 A,B,C 都是 的子集,它们可以简单的表示为 A={6},B={2,4,6,8,10},C={1,2,3,4,5 }。 又因为 是所有基本事件所组成,因而在任一次试验中,必然要出 现重的某一基本事件 ,即 。也就是在试验中, 必然会发 生,所以今后又 来代表一次必然事件。 相应地,空集 可以看做是 ,也就是说 永远不可能发生,所以 是不可能事件。必然事件和不可能事件的发生与否,已经失去了“不 确定性”,因而本质上它们不是随机事件。但是为了方便起见,我们 还是把它们看作随机事件,稍后我们会理解,它们不过是随机事件的 两个极端情形而已。

一个样本空间。中,可以有很多的随机事件。概率论的任务之一, 是研究随机事件的规律,通过对较简单事件规律的研究去掌握更复杂 事件的规律。为此,需要研究事件之间的关系和事件之间的一些运算。 如果没有特别的声明,在以下的叙述中总认为样本空间。已经给定, 并且还给定了2中的一些事件,如A、B、A(I=1,2,…)等等 1.如果事件A发生必然导致事件Bf发生,则称B包含了A,或者 A是B的特款,并记作A二B或BOA。比如在前面提到过的A={球的 标号=6}这一事件发生就导致事件B{球的标号是偶数}的发生,因为摸 到标号为6的球意味着标号为偶数的球出现了,所以前者是后者的特 款,也就是后者包含了前者。 可以给上述的含意以一个直观的几何解释,设样本空间2是一个正 方形(见图1.1),A与B是两个事件也就是说是2的某两个子集。“A 发生必然导致B发生”意味着“属于A的0必然属于B”,即A中的 点全在B中,其几何图形如右所示:
一个样本空间 中,可以有很多的随机事件。概率论的任务之一, 是研究随机事件的规律,通过对较简单事件规律的研究去掌握更复杂 事件的规律。为此,需要研究事件之间的关系和事件之间的一些运算。 如果没有特别的声明,在以下的叙述中总认为样本空间 已经给定, 并且还给定了 中的一些事件,如 A、B、 Ai (I= 1,2,…)等等 1. 如果事件 A 发生必然导致事件 B f 发生,则称 B 包含了 A,或者 A 是 B 的特款,并记作 A B 或 B A。比如在前面提到过的 A={球的 标号=6}这一事件发生就导致事件 B {球的标号是偶数}的发生,因为摸 到标号为 6 的球意味着标号为偶数的球出现了,所以前者是后者的特 款,也就是后者包含了前者。 可以给上述的含意以一个直观的几何解释,设样本空间是一个正 方形(见图 1.1),A 与 B 是两个事件也就是说是 的某两个子集。“A 发生必然导致 B 发生”意味着“属于 A 的 必然属于 B”,即 A 中的 点全在 B 中,其几何图形如右所示:
A 2 由此可知,事件ACB的含意与集合论中的意义是一致的。 因为不可能事件0不含有任何0,所以对任一事件A,我们约定 OC A 2.如果有A二B,B一A同时成立,则称事件A与B相等,记作 A=B。易知,相等的两个事件A、B,总是同时发生或同时不发生。 3.“事件A与B中至少有一个发生”,这样的一个事件称作事件A 与B的并(或和),并记作A)B。他的几何表示如下: 图12
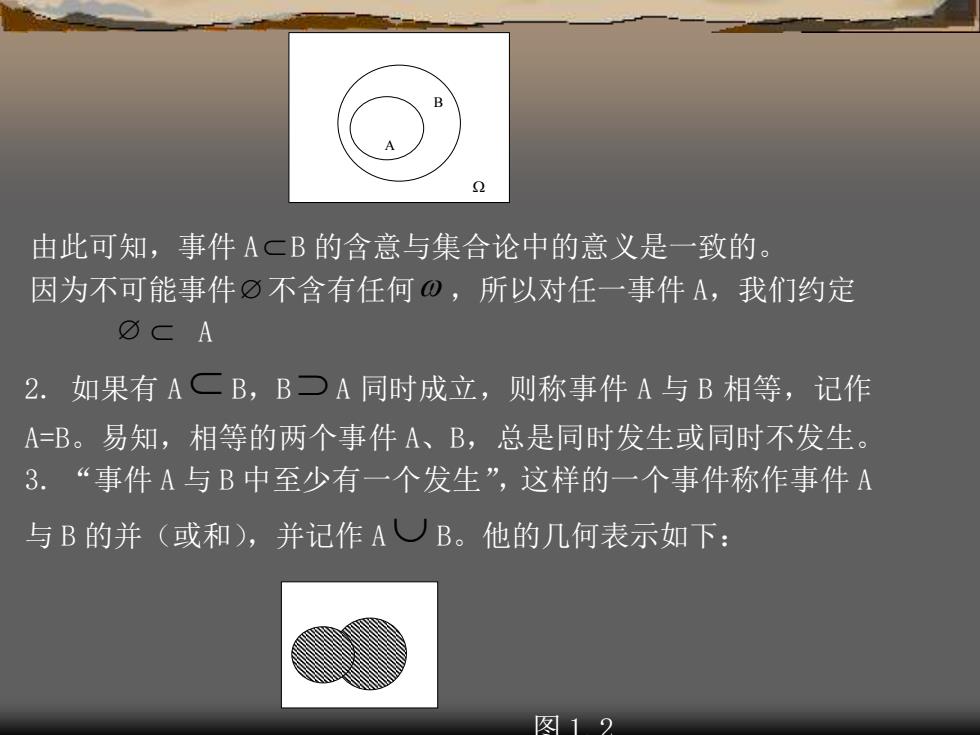
A B 由此可知,事件 A B 的含意与集合论中的意义是一致的。 因为不可能事件 不含有任何 ,所以对任一事件 A,我们约定 A 2. 如果有 A B,B A 同时成立,则称事件 A 与 B 相等,记作 A=B。易知,相等的两个事件 A、B,总是同时发生或同时不发生。 3. “事件 A 与 B 中至少有一个发生”,这样的一个事件称作事件 A 与 B 的并(或和),并记作 A B。他的几何表示如下: 图 1.2

图中的阴影部分是事件“AB”如在例1.2中,若 A={球的标号为偶数} B={球的标号≤3} 则AB={球的标号为1,2,3,4,6,8,10} 4.事件A与B同时发生“,这样的事件称作事件A与B的交(或 积),记作A⌒B(或AB),它对应图1.3种的阴影部分: 如在例1.2中,若A、B同上,则 图1.3 A⌒B={球的标号2)
图中的阴影部分是事件“AB”如在例 1.2 中,若 A={球的标号为偶数} B={球的标号≤3} 则 AB={球的标号为 1,2,3,4,,6,8,10} 4.事件 A 与 B 同时发生“,这样的事件称作事件 A 与 B 的交(或 积),记作 AB(或AB),它对应图1.3种的阴影部分: 如在例1.2中,若A、B同上,则 图 1 .3 A B={球的标号2}

5.“事件A发生而B不发生”,这样的事 件称为事件A与B的差,记作A-B,它表示 了图1.4中的阴影部分:
5.“事件A发生而B不发生” ,这样的事 件称为事件A与B的差,记作A-B,它表示 了图1.4中的阴影部分: A B

Ω 如在例1.2中,若A、B同上,则 A一B={球的标号为4,6,8,10} 6.若事件A与B不能同时发生,也就是说AB是一个不可能事件, 即AB=☑,则称事件A与B互不相容。下面的图1.2表示了这一情 形: 如在例1.2中,若 A={球的标号为偶数 B={球的标号为3} 则显然A与B不可能同时发生,即有AB=⑦,也就是说A与B互不 相容的
B A 如在例 1.2 中,若 A、B 同上,则 A—B={球的标号为 4,6,8,10} 6. 若事件 A 与 B 不能同时发生,也就是说 A B 是一个不可能事件, 即 AB=,则称事件 A 与 B 互不相容。下面的图 1.2 表示了这一情 形; 如在例 1.2 中,若 A={球的标号为偶数} B={球的标号为 3 } 则显然 A 与 B 不可能同时发生,即有 AB=,也就是说 A 与 B 互不 相容的

B 图1.5 7,若A是一个事件,令A=2一A,称A是A的对立事件或逆事 件。容易知道在一次试验中,若A发生,则A必不发生(反之亦然) 即A与4二者只能发生其中之一,并且也必然发生其中之一。因而 有 AA=☑ AUA=① 此外显然有A=A 如在例1.2中,若
A B 图 1.5 7 . 若 A 是一个事件,令 − A = — A,称 − A 是 A 的对立事件或逆事 件。容易知道在一次试验中,若 A 发生,则 − A 必不发生(反之亦然) 即 A 与 − A 二者只能发生其中之一,并且也必然发生其中之一。因而 有 A − A= A − A = 此外显然有 = A=A 如在例 1.2 中,若