
§1.4概率的公理化定义及概率的性质 一个随机试验,如果他的数学模型时古典概型,那 么描述这个试验的样本空间、事件域和概率P 已在§3种得到了解决.在古典范围内试验的结果是 有限的。当试验结果为无限时,会出现一些本质性 困难,使问题不能像有限时那么容易解决。这里讨 论具有一某种“等可能性”的一类问题。 如果我们在一个面积为S,的区域中,等可能 的取值(图1.6)设区域①中任意一区域A,如果它
§1.4 概率的公理化定义及概率的性质 gjzsj
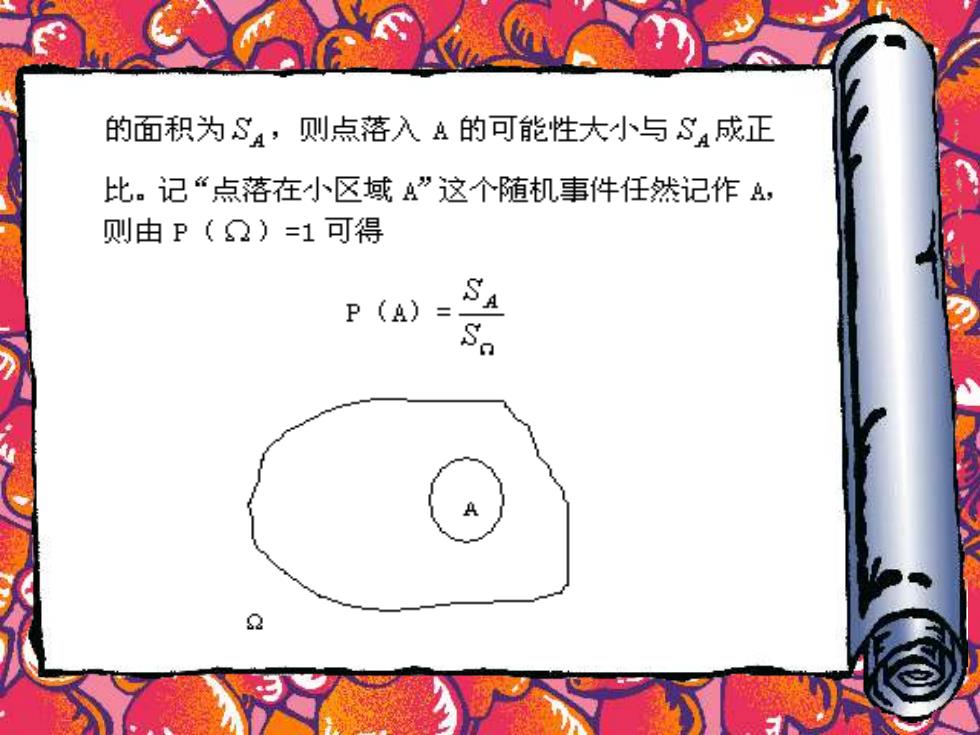
的面积为S4,则点落入A的可能性大小与S:成正 此。记“点落在小区域A”这个随机事件任然记作A, 则由P()=1可得 P(A)= S Sa A
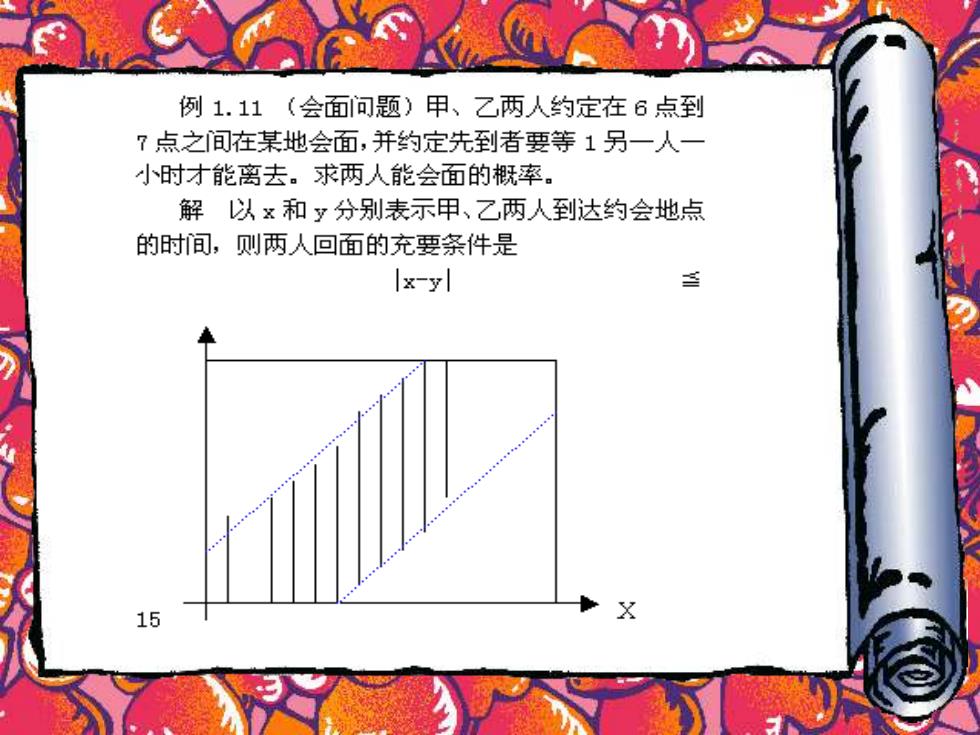
例1.11(会面问题)甲、乙两人约定在6点到 ?点之间在某地会面,并约定先到者要等1另一人一 小时才能离去。求两人能会面的慨率。 解以x和y分别表示甲、乙两人到达约会地点 的时间,则两人回面的充要条件是 -yl 15 X

在平面上建立直角坐标系图1.7。则(x,y)的 所有可能结果是边长60的正方形,而会面可能时间 是图中的阴影部分。 由等可能性质知: P(A)= S4.602-4527 Sa 602 16 例1.12浦丰投针问题。平面上画有等距离的 平行线,平行线间的距离为a(a>0),在平面任意投 掷一枚长1(1<a)的针,试求针与平行线相交的慨 率

解以x表示针的中点与最近的一条平行线的 距离,又以®表示针与此直线间的交角,知 以 0≤x≤ 2 0爸0英江 由这两式可以确定x平面上的一个矩形, 这时为了针与平行线相交,其充分条件是: x≤二sin& 2 由这个不等式表示的区域A是图中的阴影部分。 由等可能性知

-sin gaoo 0 P(A)= 2 21 P 图略(见书P24) 现在,我们比较仔细地来考察这一类投点 问题。为了方便起见,设是一个单位正方形(图 1.9),A是样本空间的一个子集。由等可能性知 P(A)= SA

这里S是A的面积。容易验证这样的概率P的 确具有非负性、规范性和有限可加性,看来问题是 轻而易举的解决了。但是,切莫高兴得太早,还有 一个非常基本的问题没有解决。从过去的讨论已经 知道,概率P是在事件域∫上有定义的集合还数, 它的非负性、规范性和有限可加性也只有在∫上才 有意义。现在我们不免要问,在上述投点试验中, 事件域∫究竟是什么?在古典概型中,已经知道∫ 可以是的一切子集的全体,很自然地会认为在投 点试验中,∫也可以是的一切子集的全体。遗憾 的是,这样的“推广”是行不通的。由于等可能性, 以知对于2的子集A有P(A)=SA,这里SA是A

的面积,因而A不能是的任意子集,至少应该是 中“具有面积”的一类子集。说到这里,读者一定 会觉得奇怪,难道在单位正方形中还有“不具有 面积”的子集吗?一点都不假,人们已经证明了这 种“不具有面积”的子集确实存在,这种集合称作 不可测集。对这一个问题的进一步讨论已经超出本 书的范围,这里我们要求读者接受Q中“不具有面 积”的子集确实存在这一事实,现在回到我们所关 心的问题上来。由前面的讨论我们知道在投点试验 中,事件域∫不能是的一切子集的全体,而只能 是的一切“具有面积”的子集的全体。容易验证, 这样的事件域∫是一个布尔代数,对于A∈∫,P(A)

=SA。也很容易验证,这样的概率P的确是∫上目 负的、规范的、有限可加的集合函数。于是,∫, P三者描述了这个投点试验。 由上述投点试验可以看到,只要构造适当的随机 试验,面积就成了概率,这就告诉我们面积具有的 性质,慨率也应该具有非负性和有限可加性,这再 一次说明了慨率应该具有非负性和有限可加性,除 此之外,还有什么值得我们注意呢? 如果在单位正方形中有一列两两互不相交的小 区域A1,A2,…,每个小区域的面积是1,S2,…, 很自然的我们可以问:这些小区域总面积是多少?

按照前面的记号,这些小区域的并可以记作 总的面积 SA 把面积了解为慨率,上式: SA i=1 在§2中已经知道慨率P的事件域£上有有限