
§1.6独立性 在上一节中我们知道了条件概率这个慨念,在 以知事件A发生的条件下,B发生的可能性味条 件慨率 P (B|A)= P(AB) P(A) 并且由此得到了一般的概率乘法公式: 事实上事件B的发生不受A的影响,也就是意味 着 P (B)=P (BA) 有此启示我们引入下述定义:
§1.6 独立性

定义1.5对任意的两个事件A、B,若 P(AB)=P(A)·P(B) 成立,则称事件A、B相互独立,简称为独立的。 这一事实读者不会感到意外,因为必然事件 与不可能事件⑦的发生与否,的确是不受任何 事件影响的,也不影响其他事件是否发生。 例题略(见书P42) 现在我们已经知道当事件A、B互不相容时,有 加法公式: P (AUB)=P (A)+P (B) 如果事件A与B互相独立,则有乘法公式P(B) =P (A)P (B)

这两个公式的外形是很类式的加法公式,而令一 个是关于积的乘法公式。由慨率的有限可加性已 知加法公式对任意有限个事件都成立,例如有、 B、C三个事件,它们两两互不相容 引例从一付52张的扑克牌中任意抽取一张, 以A表示抽出一张A,以B表示抽出一张黑桃, 问A与B是否独立? 定理、以下四件事等价: (1)事件A、B相互独立;(2)事件A、B相互独立; (3)事件A、B相互独立;(4)事件A、B相互独立。 二、多个事件的独立定义 若三个事件A、B、 C满足:
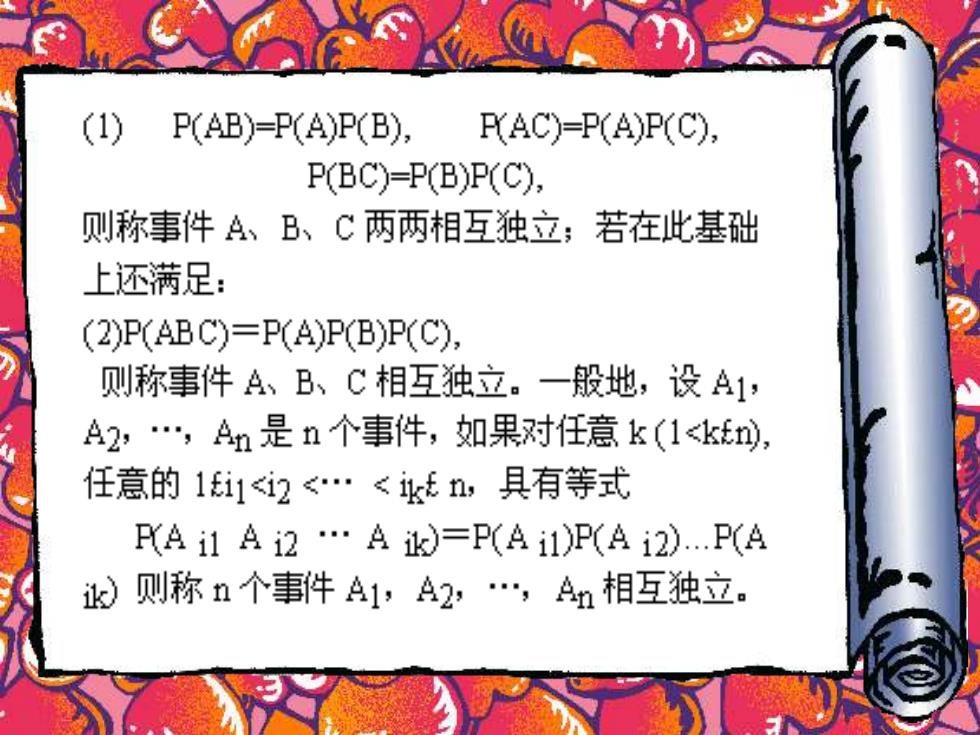
(1) P(AB)=P(A)P(B), RAC)=P(A)P(C), P(BC)=P(B)P(C), 则称事件A、B、C两两相互独立; 若在此基础 上还满足: (2)P(ABC)=P(A)P(B)P(C), 则称事件A、B、C相互独立。一般地,设A1, A2,…,An是n个事件,如果对任意k(1<kf, 任意的1i1<i2<…<kn,具有等式 P(A1A2…A=P(A1)P(Ai2)P(A )则称n个事件A1,A2,…,An相互独立

三、事件独立性的应用1、加法公式的简化:若 事件A1,A2,,A如相互独立,这时就有 P(AUBUC)=P (A)+P(B)+P(C) 由两个公式的相似外形,你可能会产生一种猜 测:如果事件A,B,C两两独立,就有乘法公式 P(AUBUC)=P(A)+P(B)+P (C) 成立。遗憾的是这个猜测一般说来并不成立。事 件A,B,C两两独立,依定义有下述三个等式: P(AB)=P(A)P(B) PBC)=PB)P(C) (1.18) P(CA)=P(C)P(A)

同时成立,但是由这三个等式并不能保证 P(ABC)=P(A)P(B)P(C) (1.19) 也一定成立.下面的例子证实了这一点 例1.22设样本空间0={w1,w2,w3,w 4)含有等可能的罡个基本事件,又 A={w1,w2) B={w1,w3) C={w1,w4) 显然有 P(A)=P(B)=P(C)=24=1/2

并且容易验证这时(1.18)的三个等式均成立,但 ABC={⊙1)} 所以 P(ABC)=1/4P(A)P(B)P(C) 反过来,由P(ABC)=P(AP(B)PC成立, 也不能保证(1.18)的三个式子一定成立(习题 1.38).为此,对三个事件的独立性就要求(1.18) 和(1.19)都成立.所以有下述定义: 定义1.6对任意三个事件A,B,C,如果有

P(AB)=P(A)P(B) PBC)=PB)P(C) P(CA)=P(C)P(A) P(ABC)=P(A)P(B)P(C) (1.20) 四个同时成立则称事件A,B,C相互独立 现在可以讨论一般的情形.设A1,A2,…,An 是n个事件如果对于任意的k(1<ksn)和任意 的一组1茶i1<i2《<ik茶n,等有等式

P(Ai1Ai2…Ai)=P(Ai1)P(Ai2)…P (A航) 〔1.21) 成立,则称A,A2…A是n个相互独立的事件 由此可知,n个事件的相互独立性,需要有 2[]=2*--1 个等式来保证 在前面的讨论中已经指出,事件的独立性 可以使得实际问题的计算得简化.下面便是生 个应用的例子

例1.23用2n个相同的元件(例如整流 二 极管)组成一个系统,有两种不同的联结 方式,第I种是先串联后并联(如图1.12 所示);第Ⅱ所示是先并联后串联(如图 1.13所示). 如果各个元件能否正常工件是相互独立 的,每个元件能正常工件的概率为(元件 或系统能正常工件的概率通常称为可靠 度),请你比较一下两个系统那一个更可 靠一些?
例 1.23 用2n个相同的元件(例如整流二 极管)组成一个系统,有两种不同的联结 方式,第Ⅰ种是先串联后并联(如图1.12 所示);第Ⅱ所示是先并联后串联(如图 1.13所示). 如果各个元件能否正常工件是相互独立 的,每个元件能正常工件的概率为r(元件 或系统能正常工件的概率通常称为可靠 度),请你比较一下两个系统那一个更可 靠一些?