
统计推断方法案例解析! 背景:有一个老人到商店花了一元钱买了一把扇子。过了一晚上,老人觉得一元钱的扇子不好,于是回到 原来的商店把一元钱的扇子退回去,拿了一把二元钱扇子准备走,店员就叫住他,叫他补交一元钱。老人 于是争菏道:我昨天给了你一元钱,我今天又把一元钱的扇子交给你,不是刚好两元钱吗?这把店员弄糊 涂了,只好让老人把两元钱的扇子拿回去。结果老人如法炮制,每过一天老人就去商店买一把价钱比前 把贵一倍的扇子,而花的钱只有一元。?? 问题:请应用统计推断方法分析这种“资产增值现象”? 其他回答 老人说给过一块钱,加扇子相当于的另一块钱,于是拿走两块钱的扇子 如法炮制:给过一块钱,给过一块钱扇子,现给两块钱扇子,拿四块钱扇子, 以此类推一 资产增值的结论成立的前提是,老人给过的东西(包括钱和扇子)可以不断地重复使用,就等于最初那- 块钱用了N次变成N块钱,整个过程就如同是同一个等比数列,出现N次,每次比上一次多一项,如此 述方法(次多一项的等比数刚指述这种现象,解释就不会了。个人 从现实上说那是不对的,那一块钱不同于放在银行里的钱,不能这样增值的,简单来说不能重复使用,不 然世界就乱套了, 第五章统计量及其分布 例5.0.1某公司要采购一批产品,每件产品不是合格品就是不合格品,但该批产品总有 个不合格品率P。由此,若从该批产品中随机抽取一件,用x表示这一批产品的不合格 数,不难看出x服从一个二点分布(1,P,但分布中的参数P是不知道的。一些问题: (D的大小如何: (2)D大概落在什么范围内: (3)能否认为p满足设定要求(如p≤0.05) §5.1 总体与个体 总体的三层含义:研究对象的全体:数据:分布 例5.1.1考察某厂的产品质量,以0记合格品,以1记不合格品,则 总体={该厂生产的全部合格品与不合格品} ={由0或1组成的一堆数} 若以P表示这堆数中1的比例(不合格品率),则该总体可由一个二点分布表示: 1
1 统计推断方法 案例解析! 背景:有一个老人到商店花了一元钱买了一把扇子。过了一晚上,老人觉得一元钱的扇子不好,于是回到 原来的商店把一元钱的扇子退回去,拿了一把二元钱扇子准备走,店员就叫住他,叫他补交一元钱。老人 于是争辩道:我昨天给了你一元钱,我今天又把一元钱的扇子交给你,不是刚好两元钱吗?这把店员弄糊 涂了,只好让老人把两元钱的扇子拿回去。结果老人如法炮制,每过一天老人就去商店买一把价钱比前一 把贵一倍的扇子,而花的钱只有一元。? ? 问题:请应用统计推断方法分析这种“资产增值现象”? 其他回答 老人说给过一块钱,加扇子相当于的另一块钱,于是拿走两块钱的扇子 如法炮制:给过一块钱,给过一块钱扇子,现给两块钱扇子,拿四块钱扇子, 以此类推~~~~~ 资产增值的结论成立的前提是,老人给过的东西(包括钱和扇子)可以不断地重复使用,就等于最初那一 块钱用了 N 次变成 N 块钱,整个过程就如同是同一个等比数列,出现 N 次,每次比上一次多一项,如此 而已。 我就只能用上述方法(每次多一项的等比数列)描述这种现象,解释就不会了。个人认为确实从逻辑上说 从现实上说那是不对的,那一块钱不同于放在银行里的钱,不能这样增值的,简单来说不能重复使用,不 然世界就乱套了。 第五章 统计量及其分布 例 5.0.1 某公司要采购一批产品,每件产品不是合格品就是不合格品,但该批产品总有一 个不合格品率 p 。由此,若从该批产品中随机抽取一件,用 x 表示这一批产品的不合格 数,不难看出 x 服从一个二点分布 b(1 , p), 但分布中的参数 p 是不知道的。一些问题: (1) p 的大小如何; (2) p 大概落在什么范围内; (3) 能否认为 p 满足设定要求(如 p 0.05)。 §5.1 总体与个体 总体的三层含义:研究对象的全体;数据;分布 例 5.1.1 考察某厂的产品质量,以 0 记合格品,以 1 记不合格品,则 总体 = {该厂生产的全部合格品与不合格品} = {由 0 或 1 组成的一堆数} 若以 p 表示这堆数中 1 的比例(不合格品率),则该总体可由一个二点分布表示:

0 P 1-p p 比如:两个生产同类产品的工厂的产品的总体分布: n 1 0.983 0.007 X 0 1 0.915 0.085 例5.12在二十世纪七十年代后期,美国消费者购买日产SONY彩电的热情高于购买美 SONY彩电,原因何在? 原因在于总体的差异上! 1979年4月17日日本《朝日新闻》刊登调查报告指出N(m,(5/3)2,日产SONY彩 电的彩色浓度服从正态分布,而美产SONY彩电的彩色浓度服从(m5,m+5)上的均 匀分布。 >(一)画分布图: >表5.11各等级彩电的比例(%) 等级 1 333333333 L日产 683 271 43 0.3 5.1.2样本 样品、样本、样本量:样本具有两重性 一方面 由于样本是从总体中随机抽取的,抽取前无法预知它们的数值,因此,样 本是随机变量,用大写字母X,X2,,Xn表示: ·另一方面,样本在抽取以后经观测就有确定的观测值,因此,样本又是一组数值 此时用小写字母x礼,2,,x表示是恰当的。 ·简单起见,无论是样本还是其观测值,样本一般均用x1,2…m表示,应能从上 下文中加以区别。 例5.1.3啤酒厂生产的瓶装啤酒规定净含量为640克。由于随机性,事实上不可能使得所 有的啤酒净含量均为640克。现从某厂生产的啤酒中随机抽取10瓶测定其净含量,得到如 下结果: 641,635,640,637,642,638,645,643,639,640 这是一个容量为10的样本的观测值,对应的总体为该厂生产的瓶装啤酒的净含量
2 X 0 1 P 1-p p 比如:两个生产同类产品的工厂的产品的总体分布: X 0 1 P 0.983 0.007 X 0 1 P 0.915 0.085 例5.1.2 在二十世纪七十年代后期,美国消费者购买日产 SONY 彩电的热情高于购买美 产 SONY 彩电,原因何在? 原因在于总体的差异上! ➢ 1979 年 4 月 17 日日本《朝日新闻》刊登调查报告指出 N(m, (5/3)2),日产 SONY 彩 电的彩色浓度服从正态分布,而美产 SONY 彩电的彩色浓度服从(m−5 , m+5)上的均 匀分布。 ➢ (一)画分布图: ➢ 表 5.1.1 各等级彩电的比例(%) 等级 I II III IV 美产 33.3 33.3 33.3 0 日产 68.3 27.1 4.3 0.3 5.1.2 样本 样品、样本、样本量: 样本具有两重性 • 一方面,由于样本是从总体中随机抽取的,抽取前无法预知它们的数值,因此,样 本是随机变量,用大写字母 X1, X2, …, Xn 表示; • 另一方面,样本在抽取以后经观测就有确定的观测值,因此,样本又是一组数值。 此时用小写字母 x1, x2, …, xn 表示是恰当的。 • 简单起见,无论是样本还是其观测值,样本一般均用 x1, x2,… xn 表示,应能从上 下文中加以区别。 例 5.1.3 啤酒厂生产的瓶装啤酒规定净含量为 640 克。由于随机性,事实上不可能使得所 有的啤酒净含量均为 640 克。现从某厂生产的啤酒中随机抽取 10 瓶测定其净含量,得到如 下结果: 641, 635, 640, 637, 642, 638, 645, 643, 639, 640 这是一个容量为 10 的样本的观测值,对应的总体为该厂生产的瓶装啤酒的净含量
这样的样本称为完全样本。 表5.1.2100只元件的寿命数据 寿命范围 元件数 寿命范围元件数 寿命范围 元件数 (024 119221616 3844081 (2448 (216240 (408 4327 (48721 (2402643 (432456 (72960 (26428815 14564801 (961201 28831215 4805041 (120144 312336 3 528 (144168] 5 (33636015 (5285521 (16819214 (36018411 >552 13 表5.1.2中的样本观测值没有具体的数值,只有一个范围,这样的样本称为分组样本。 样本的要求:简单随机样本 要使得推断可靠,对样本就有要求,使样本能很好地代表总体。通常有如下两个 求, >随机性:总体中每一个个体都有同等机会被选入样本一x与总体X有相 同的分布 >独立性:样本中每一样品的取值不影响其它样品的取值…x1,x2,, n相互独立。 用简单随机抽样方法得到的样本称为简单随机样本,也简称样本 于是,样本x1,x2,,xn可以看成是独立同分布(d)的随机变量,其共同分布 即为总体分布。 设总体X具有分布函数Fx,xl,x2,,xm为取自该总体的容量为n的样本,则 样本联合分布函数为 Fx,,x)=ΠF(x 总体分为有限总体与无限总体 实际中总体中的个体数大多是有限的。当个体数充分大时,将有限总体看作无限总体是 一种合理的抽象。 对无限总体,随机性与独立性容易实现,困难在于排除有意或无意的人为干扰 对有限总体,只要总体所含个体数很大,特别是与样本量相比很大,则独立性也可基 得到满足。 3
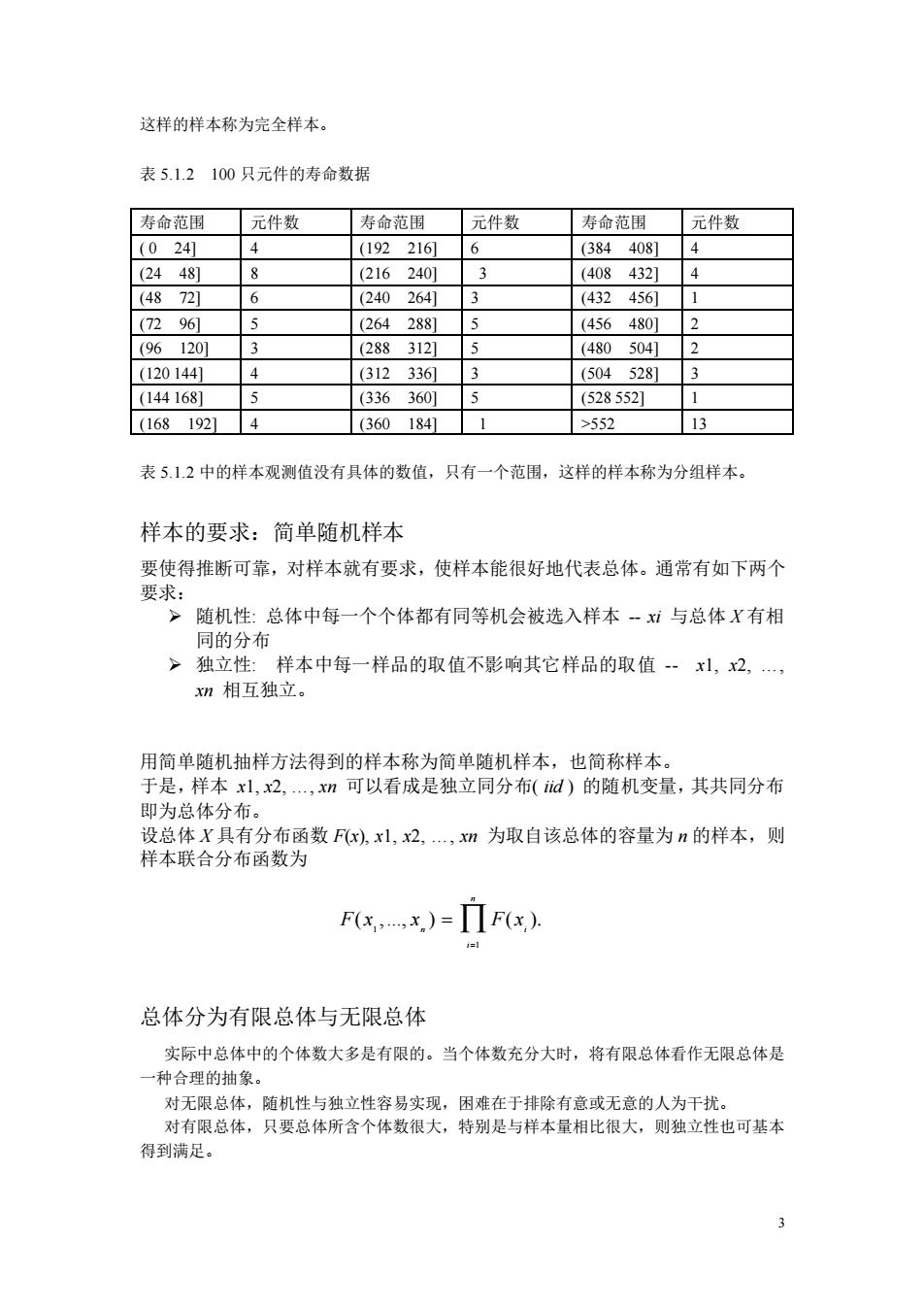
3 这样的样本称为完全样本。 表 5.1.2 100 只元件的寿命数据 寿命范围 元件数 寿命范围 元件数 寿命范围 元件数 ( 0 24] 4 (192 216] 6 (384 408] 4 (24 48] 8 (216 240] 3 (408 432] 4 (48 72] 6 (240 264] 3 (432 456] 1 (72 96] 5 (264 288] 5 (456 480] 2 (96 120] 3 (288 312] 5 (480 504] 2 (120 144] 4 (312 336] 3 (504 528] 3 (144 168] 5 (336 360] 5 (528 552] 1 (168 192] 4 (360 184] 1 >552 13 表 5.1.2 中的样本观测值没有具体的数值,只有一个范围,这样的样本称为分组样本。 样本的要求:简单随机样本 要使得推断可靠,对样本就有要求,使样本能很好地代表总体。通常有如下两个 要求: ➢ 随机性: 总体中每一个个体都有同等机会被选入样本 -- xi 与总体 X 有相 同的分布 ➢ 独立性: 样本中每一样品的取值不影响其它样品的取值 -- x1, x2, …, xn 相互独立。 用简单随机抽样方法得到的样本称为简单随机样本,也简称样本。 于是,样本 x1, x2, …, xn 可以看成是独立同分布( iid ) 的随机变量,其共同分布 即为总体分布。 设总体 X 具有分布函数 F(x), x1, x2, …, xn 为取自该总体的容量为 n 的样本,则 样本联合分布函数为 总体分为有限总体与无限总体 实际中总体中的个体数大多是有限的。当个体数充分大时,将有限总体看作无限总体是 一种合理的抽象。 对无限总体,随机性与独立性容易实现,困难在于排除有意或无意的人为干扰。 对有限总体,只要总体所含个体数很大,特别是与样本量相比很大,则独立性也可基本 得到满足。 1 1 ( ,..., ) ( ). n n i i F x x F x = =

例5.1.5设有一批产品共N个,需要进行抽样检验以了解其不合格品率P。现从中采取不 放回抽样抽出2个产品,这时,第二次抽到不合格品的概率依赖于第一次抽到的 是否是不合格品,如果第一次抽到不合格品,则 P(2=1Ix1=I)=Np-1)/N-I) 而若第一次抽到的是合格品,则第二次抽到不合格品的概率为 P(x2=1|x1=0)=(Wp)/N-1) 显然 ,如此得到的样本不是简单随机样本。但是,当N很大时 我们可以看到上述两 种情形的概率都近似等于p。所以当N很大,而n不大(一个经验法则是n/N≤0.1)时 可以把该样本近似地看成简单随机样本。 思考:若总体的密度函数为风,则其样本的(联合)密度函数是什么?
4 例5.1.5 设有一批产品共 N 个,需要进行抽样检验以了解其不合格品率 p。现从中采取不 放回抽样抽出 2 个产品,这时,第二次抽到不合格品的概率依赖于第一次抽到的 是否是不合格品,如果第一次抽到不合格品,则 P(x2 = 1 | x1 = 1) = (Np−1)/(N−1) 而若第一次抽到的是合格品,则第二次抽到不合格品的概率为 P(x2 = 1 | x1 = 0) = (Np)(N−1) 显然,如此得到的样本不是简单随机样本。但是,当 N 很大时,我们可以看到上述两 种情形的概率都近似等于 p 。所以当 N 很大,而 n 不大(一个经验法则是 n N 0.1)时 可以把该样本近似地看成简单随机样本。 思考: 若总体的密度函数为 p(x),则其样本的(联合)密度函数是什么?

§5.2样本数据的整理与显示 5.2.1经验分布函数 设xL,x2,,m是取自总体分布函数为Fx)的样本,若将样本观测值由小到大 进行排列,为x(1),x(2),,x),则称xI),2),,xm)为有序样本, 用有序样本定义如下函数 0, X <x) Fn(x)=k1n,xw,≤x<k4, k=1,2,n-1 xw)≤x 则Fx)是一非减右连续函数,且满足 Fmo-)=0和FMo+)=1 由此可见,Fx)是一个分布函数,并称Fx)为经验分布函数。 例5.2.1某食品厂生产听装饮料,现从生产线上随机抽取5听饮料,称得其净重(单位:克) 351347355344351 这是一个容量为5的样本,经排序可得有序样本: x1)=344,2)=347,3351,x4)=354,5=355 其经验分布函数为 0 x<344 02. 344≤r<347 Fn(x)= 347≤x<351 0.8 344≤x<347 1, x2355 由伯努里大数定律:只要n相当大,Fx)依概率收敛于Fx)。 更深刻的结果也是存在的,这就是格里纹科定理 定理5.2.』(格里纹科定理)设xl,x2,m是取自总体分布函数为Fx)的样本,F)是其经 验分布函数,当n→0时,有 P{suplFn(x)-Fx→0=1 格里纹科定理表明:当n相当大时,经验分布函数是总体分布函数Fx)的一个良好的近似 经典的统计学中一切统计推断都以样本为依据,其理由就在于此
5 §5.2 样本数据的整理与显示 5.2.1 经验分布函数 设 x1, x2, …, xn 是取自总体分布函数为 F(x)的样本,若将样本观测值由小到大 进行排列,为 x(1), x(2), …, x(n),则称 x(1), x(2), …, x(n) 为有序样本, 用有序样本定义如下函数 则 Fn(x)是一非减右连续函数,且满足 Fn(−) = 0 和 Fn(+) = 1 由此可见,Fn(x)是一个分布函数,并称 Fn(x)为经验分布函数。 例 5.2.1 某食品厂生产听装饮料,现从生产线上随机抽取 5 听饮料,称得其净重(单位:克) 351 347 355 344 351 这是一个容量为 5 的样本,经排序可得有序样本: x(1)= 344, x(2)= 347, x(3)= 351, x(4)= 354, x(5)= 355 其经验分布函数为 0 , x < 344 0.2, 344 x < 347 Fn(x) = 0.4, 347 x < 351 0.8, 344 x < 347 1, x 355 由伯努里大数定律:只要 n 相当大,Fn(x)依概率收敛于 F(x) 。 更深刻的结果也是存在的,这就是格里纹科定理。 定理 5.2.1(格里纹科定理) 设 x1,x2,…,xn 是取自总体分布函数为 F(x)的样本, Fn(x) 是其经 验分布函数,当 n→时,有 PsupFn(x) − F(x)→0 = 1 格里纹科定理表明:当 n 相当大时,经验分布函数是总体分布函数 F(x)的一个良好的近似。 经典的统计学中一切统计推断都以样本为依据,其理由就在于此。 (1) ( ) ( 1) ( ) 0, < ( ) / , , 1,2,..., 1 1, k k n n x x F x k n x x x k n x x + = = −