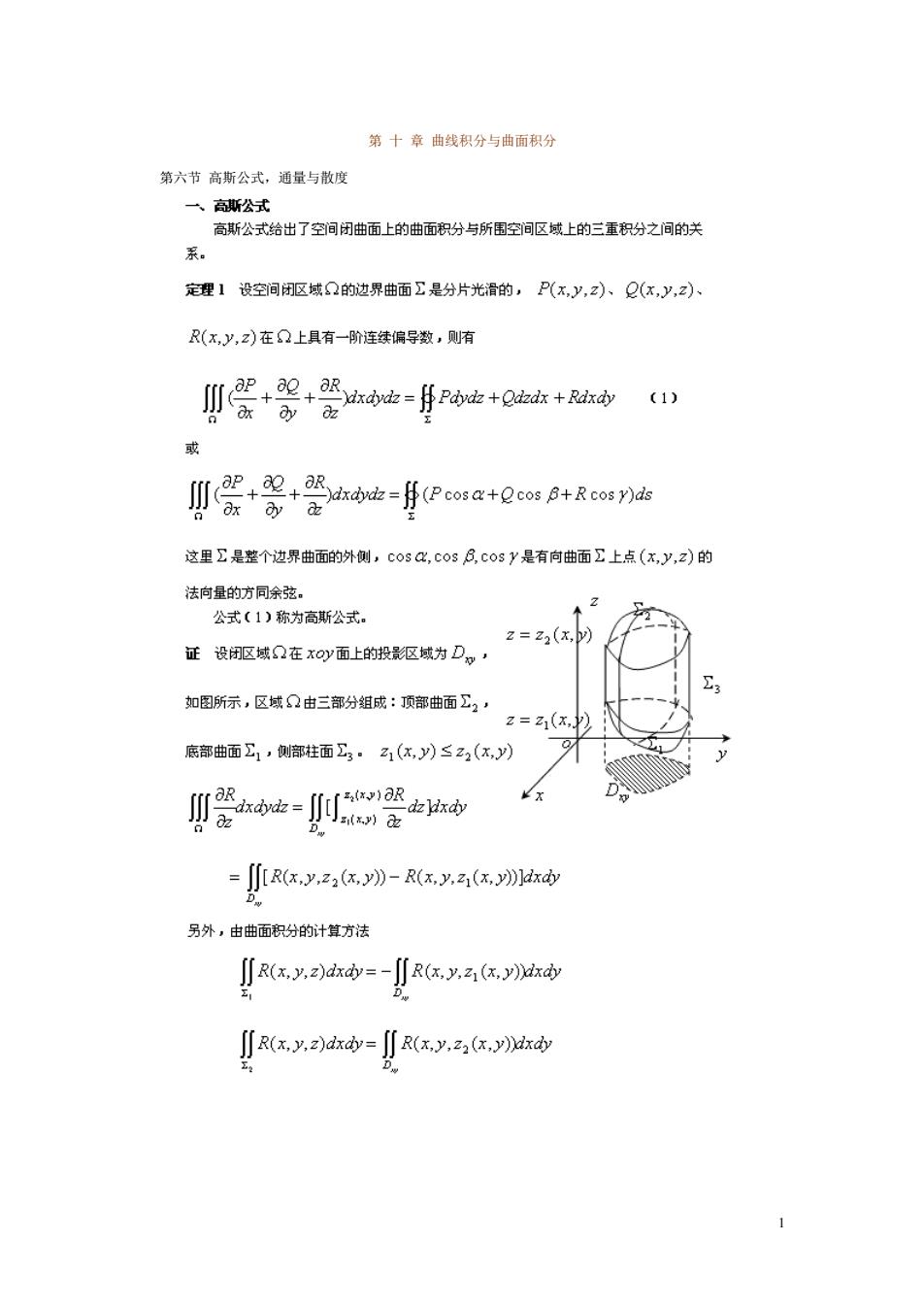
第十章曲线积分与曲而积分 第六节高斯公式,通量与散度 一高斯公式 高斯公式给出了空问闭曲面上的曲面积分与所围空问区城上的三重积分之间的关 系。 定理1设空间闭驱域Q的边界曲面工是分片光滑的,P(x,y,z)、2(x,y,z)、 R(x,y,z)在Q上具有一阶连续偏导数,则有 ∬婴+号+婴h=手P+0咖+a本u 或 ∬蛋+号空n4=fPca+ecog+Rcon油 这里∑是整个边界曲面的外侧,co3心,co3及,cosy是有向曲面工上点(x,y,z)的 2=23(x, 正设闭区城Q在xOy面上的投最影驱域为D。, 如图所示,区城2由三部分组成:顶部曲面工2, z=31(x,) 廊部曲面1,侧部柱面3·乙1(x,)≤z2(x,y)) 翠-h [[[R(x.y.z(x.))-R(x.y.z(x.)xdy 另外,由曲面积分的计算方法 ∬Rxy=-R(xya(y ∬(xy2h=∬Rxy.z.hw
1 第 十 章 曲线积分与曲面积分 第六节 高斯公式,通量与散度

刂R(y2山=0(因工,在xy上的投影为0,由曲面积分的淀义知) 从而∬R(x,y,2)dx=JR(x,y,22么,y》-R(x,y,a(x,y》x 数有∬dt=手x,yh中 类似地 ∬边=月Px%到冷2,∬t=月ex,a 因此有高斯公式(1)成立。 注当P=x,Q=y,R=z时 V=∬ak恤=f动地+hx+h 例1计笪I=∬(x+1)地+2dx+d欧d山,工为四面体OABC的外侧,平 面ABC的方程为x+y+z=1. 整厚s∬2如法- 例2计算j小(2+x刀d也-zdk中,其中工是旋转抛物 面2=号(x2+y)介于2=0及及2=2之间的部分的下创。 解P=z2+x,2=0,R=-2 K 设:z=2(x2+y2≤4)的上侧 ∬小e2+-z中+∬2+t-z=∬a-0=0 所以 ∬e2+x恤-zdx=-j∬e2+xdb-zdxy
2

=-∬[(4+x)0-2]xdy=8x 二通量与酸度 设有向量场A=P(x,y,z)+Q(x,y,z)j+R(x,y,z)E,其中P,Q,R具有 阶注珠偏导发,工为场内的一片有向曲面,则肥+2+迟叫散的量场A在点 dx dy dz (x,y,2)处的散度,记为v,即 积分Pd+Qddr+Rdxdy叫做向量场A通过有向曲面工指定侧的通量〔或 流量。 例3设f(x,y,z)=x2+yhz,求v(gad) 解gra=2i+hzj+兰e,(grad)=2-为 例4求向量场A=(2x+3z)i+(z+)方+0y2+22)话流肉工外侧的通量其 中工为球心在(3,-1,2)半径为R=3的球面。 解通是 ∬2x+3出+(z+0ax+02+2a)dk中4*∬5=180r 3
3