
历竖毛子代拔七学 XIDIAN UNIVERSITY 平面图的概念与性质 数学与统计学院应用数学系 张欣
平面图的概念与性质 数学与统计学院应用数学系 张 欣

历些毛子种枝大学 XIDIAN UNIVERSITY (一)、平面图的概念 图的平面性问题是图论典型问题之一。生活中许多问题都与该问题有关。 例子1:电路板设计问题 在电路板设计时,需要考虑的问题之一是连接电路元件间的导线间不能交 叉。否则,当绝缘层破损时,会出现短路故障。 显然,电路板可以模型为一个图,“要求电路元件间连接导线互不交叉”, 对应于“要求图中的边不能相互交叉
图的平面性问题是图论典型问题之一。生活中许多问题都与该问题有关。 (一)、平面图的概念 例子1:电路板设计问题 在电路板设计时,需要考虑的问题之一是连接电路元件间的导线间不能交 叉。否则,当绝缘层破损时,会出现短路故障。 显然,电路板可以模型为一个图,“要求电路元件间连接导线互不交叉”, 对应于“要求图中的边不能相互交叉

历安毛子代枚大学 XIDIAN UNIVERSITY 例子2:空调管道的设计 某娱乐中心有6个景点,位置分布如下图。 A4 分析者认为:(1)A与A4,(2)A2与A5,(3)A3与A6间人流较少,无需铺设空 调管道;其它景点之间人流量大,必须投资铺设空调管道,但要求空调管道间 不能交叉。如何设计?
例子2:空调管道的设计 某娱乐中心有6个景点,位置分布如下图。 A1 A4 A5 A3 A A2 6 分析者认为:(1) A1与A4 , (2) A2与A5 , (3) A3与A6间人流较少,无需铺设空 调管道;其它景点之间人流量大,必须投资铺设空调管道,但要求空调管道间 不能交叉。如何设计?

历些毛子种枝大皇 XIDIAN UNIVERSITY 如果把每个景点分别模型为一个点,景点间连线,当且仅当两景点间要铺 设空调管道。那么,上面问题直接对应的图为: 于是,问题转化为:能否把上图画在平面上,使得边不会相互交叉?
如果把每个景点分别模型为一个点,景点间连线,当且仅当两景点间要铺 设空调管道。那么,上面问题直接对应的图为: A6 A5 A4 A3 A2 A1 于是,问题转化为:能否把上图画在平面上,使得边不会相互交叉?
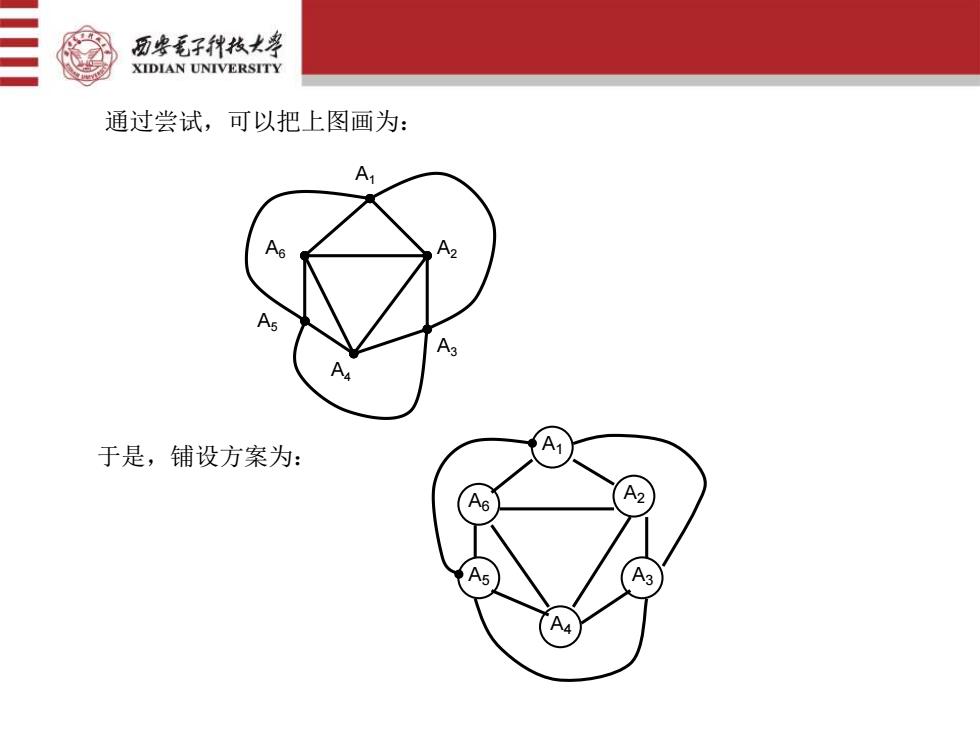
历安毛子代枚大学 XIDIAN UNIVERSITY 通过尝试,可以把上图画为: A A A AA 于是,铺设方案为: A1 Ao A2 A3
通过尝试,可以把上图画为: 于是,铺设方案为: A6 A5 A4 A3 A2 A1 A1 A4 A5 A3 A A2 6

历些毛子种枝大皇 XIDIAN UNIVERSITY 例子3:3间房子和3种设施问题 问题:要求把3种公用设施(煤气,水和电)分别用煤气管道、水管和电线连 接到3间房子里,要求任何一根线或管道不与另外的线或管道相交,能否办到? 上面问题可以模型为如下图: H1 H2 H3 问题转化为,能否把上图画在平面上,使得边与边之间不会交叉?
问题:要求把3种公用设施(煤气,水和电)分别用煤气管道、水管和电线连 接到3间房子里,要求任何一根线或管道不与另外的线或管道相交,能否办到? 例子3:3间房子和3种设施问题 上面问题可以模型为如下图: H1 H2 H3 G W E 问题转化为,能否把上图画在平面上,使得边与边之间不会交叉?

历安毛子代枚大学 XIDIAN UNIVERSITY 上面的例子都涉及同一个图论问题:能否把一个图画在平面上,使得边与 边之间没有交叉? 针对这一问题,我们引入如下概念 定义1如果能把图G画在平面上,使得除顶点外,边与边之间没有交叉,称G 可以嵌入平面,或称G是可平面图。可平面图G的边不交叉的一种画法,称为G 的一种平面嵌入,G的平面嵌入表示的图称为平面图。 G H2 H3 H3 H1 H2 图G 图G的平面嵌入
上面的例子都涉及同一个图论问题:能否把一个图画在平面上,使得边与 边之间没有交叉? 针对这一问题,我们引入如下概念 定义1 如果能把图G画在平面上,使得除顶点外,边与边之间没有交叉,称G 可以嵌入平面,或称G是可平面图。可平面图G的边不交叉的一种画法,称为G 的一种平面嵌入,G的平面嵌入表示的图称为平面图。 H1 H2 H3 G W E 图G H3 H1 H2 G W E 图G的平面嵌入

历安毛子绑枚大学 XIDIAN UNIVERSITY 注: (1)可平面图概念和平面图概念有时可以等同看待: (2)图的平面性问题主要涉及如下几个方面:1)平面图的性质;2)平面图 的判定;3)平面嵌入方法(平面性算法);4)涉及图的平面性问题的拓扑不变量。 由图的平面性问题研究引申出图的一般嵌入性问题的研究,形成了拓扑图 论的主要内容。 历史上,波兰数学家库拉托斯基、美国数学家惠特尼、生于英国的加拿大 数学家托特,我国数学家吴文俊等都在拓扑图论中有过精湛的研究
注: (1) 可平面图概念和平面图概念有时可以等同看待; (2) 图的平面性问题主要涉及如下几个方面:1) 平面图的性质;2) 平面图 的判定;3) 平面嵌入方法(平面性算法) ;4)涉及图的平面性问题的拓扑不变量。 由 图的平面性问题研究引申出图的一般嵌入性问题的研究,形成了拓扑图 论的主要内容。 历史上,波兰数学家库拉托斯基、美国数学家惠特尼、生于英国的加拿大 数学家托特,我国数学家吴文俊等都在拓扑图论中有过精湛的研究

历安毛子代枚大学 XIDIAN UNIVERSITY (二)、平面图性质 定义2 (1)一个平面图G把平面分成若干连续的部分,这些连续的部分称为 G的区域,或G的一个面。G的面组成的集合用Φ表示。 (2)面积有限的区域称为平面图G的内部面,否则称为G的外部面。 平面图G 在上图G中,共有4个面。其中f4是外部面,其余是内部面。Φ={f1,f2,f, f4}
(二)、平面图性质 定义2 (1)一个平面图G把平面分成若干连续的部分,这些连续的部分称为 G的区域,或G的一个面。G的面组成的集合用Φ表示。 在上图G中,共有4个面。其中f4是外部面,其余是内部面。Φ={f1 , f2 , f3 , f4}。 平面图G f1 f3 f2 f4 (2)面积有限的区域称为平面图G的内部面,否则称为G的外部面

历零毛子代枚大兽 XIDIAN UNIVERSITY (3)在G中,顶点和边都与某个给定区域关联的子图,称为该面的边界。某 面f的边界中含有的边数(割边计算2次)称为该面f的度数,记为deg(f)。 平面图G 在上图中,绿色边在G中的导出子图为面长的边界。 deg()=1 deg()=3 deg()=6 deg()=6 1、平面图的度数公式
(3)在G中,顶点和边都与某个给定区域关联的子图,称为该面的边界。某 面 f 的边界中含有的边数(割边计算2次)称为该面f 的度数, 记为deg ( f )。 平面图G f1 f3 f2 f4 在上图中,绿色边在G中的导出子图为面 f3 的边界。 deg( ) 1 1 f = deg( ) 3 2 f = deg( ) 6 3 f = deg( ) 6 4 f = 1、平面图的度数公式