
本科图论讨论班(六) 组合零点定理及其应用 Combinatorial Nullstellensatz
本科图论讨论班(六) 组合零点定理及其应用 Combinatorial Nullstellensatz
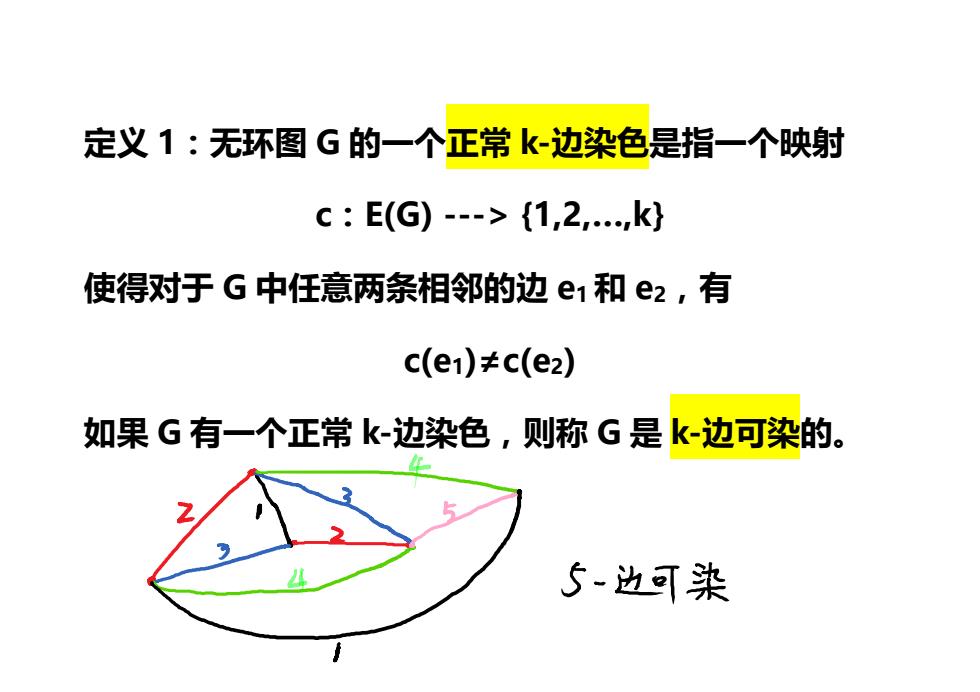
定义1:无环图G的一个正常k-边染色是指一个映射 c:E(G)-->{1,2,,k} 使得对于G中任意两条相邻的边e1和e2,有 c(e1)≠c(e2) 如果G有一个正常k-边染色,则称G是k-边可染的。 5-边可染
定义 1:无环图 G 的一个正常 k-边染色是指一个映射 c:E(G) ---> {1,2,…,k} 使得对于 G 中任意两条相邻的边 e1和 e2,有 c(e1)≠c(e2) 如果 G 有一个正常 k-边染色,则称 G 是 k-边可染的
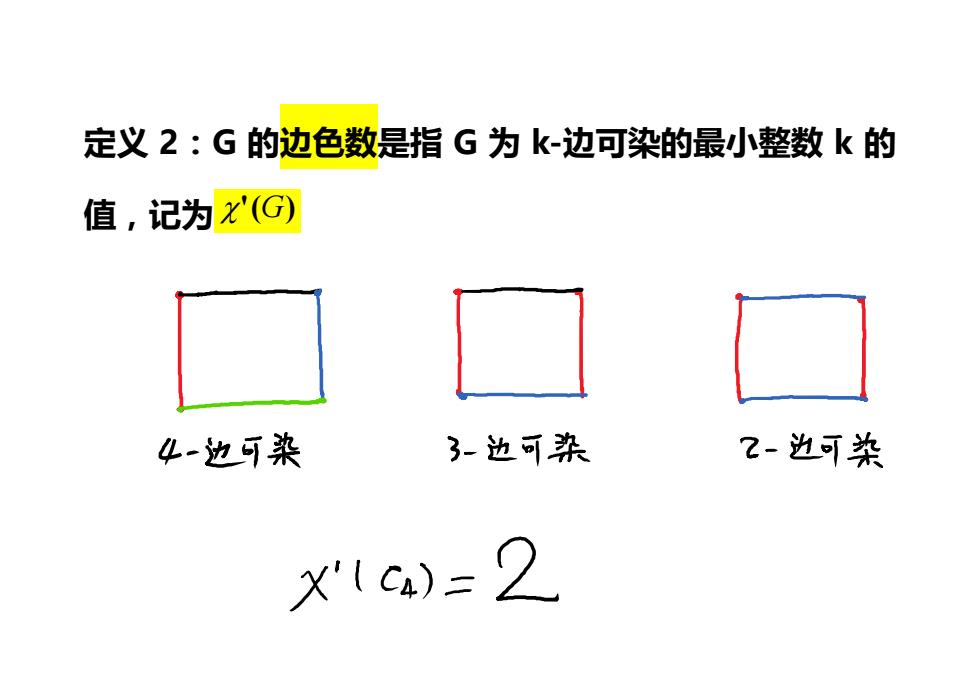
定义2:G的边色数是指G为k-边可染的最小整数k的 值,记为X'(G) -边可染 3-边可染 ?-边可柒 X'(c4)=2
定义 2:G 的边色数是指 G 为 k-边可染的最小整数 k 的 值,记为 '(G)
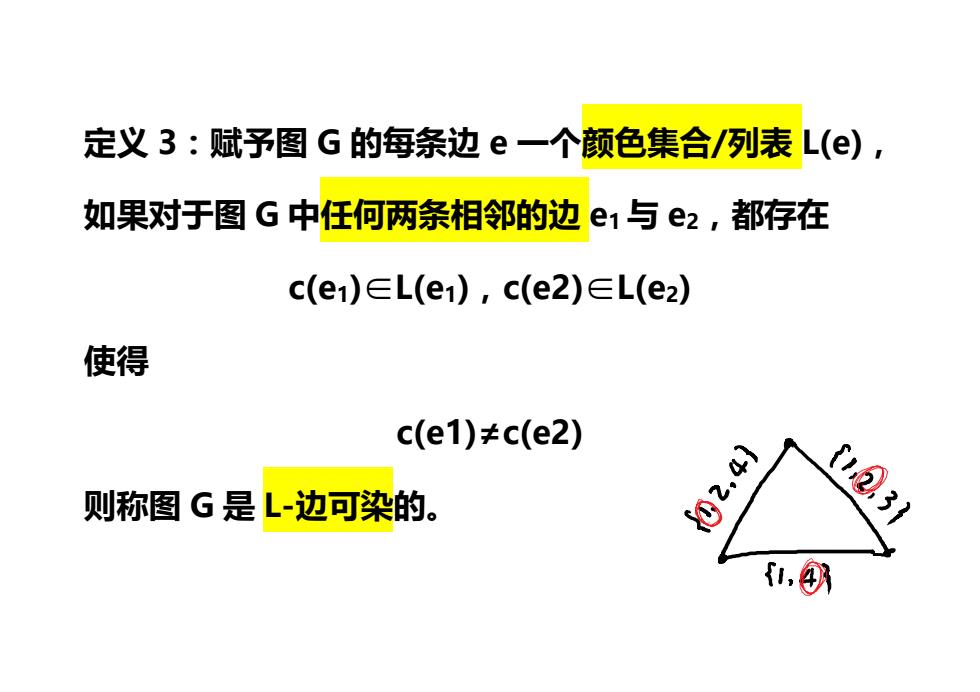
定义3:赋予图G的每条边e一个颜色集合/列表L(e), 如果对于图G中任何两条相邻的边e1与e2,都存在 c(e)∈L(e),c(e2)∈L(e2) 使得 c(e1)≠c(e2) 则称图G是L-边可染的。 02,4 ②3) ,④
定义 3:赋予图 G 的每条边 e 一个颜色集合/列表 L(e), 如果对于图 G 中任何两条相邻的边 e1与 e2,都存在 c(e1)∈L(e1),c(e2)∈L(e2) 使得 c(e1)≠c(e2) 则称图 G 是 L-边可染的
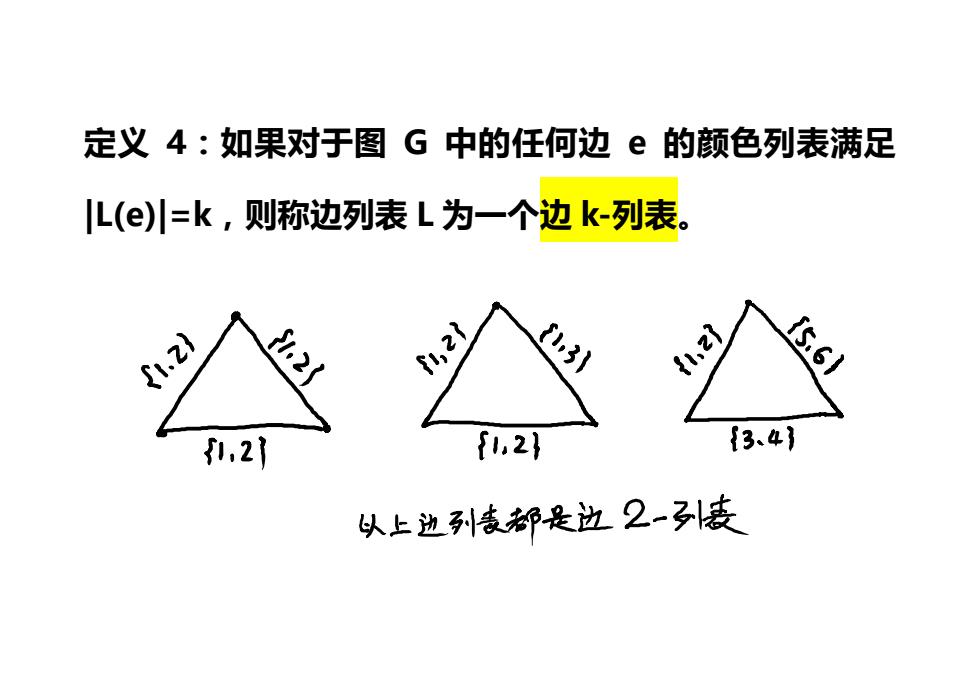
定义4:如果对于图G中的任何边e的颜色列表满足 L(e川=k,则称边列表L为一个边k-列表。 .2 ,2 13 5.6 1,21 f1.2} f3、4 以上边列表都是边2-☑引废
定义 4:如果对于图 G 中的任何边 e 的颜色列表满足 |L(e)|=k,则称边列表 L 为一个边 k-列表
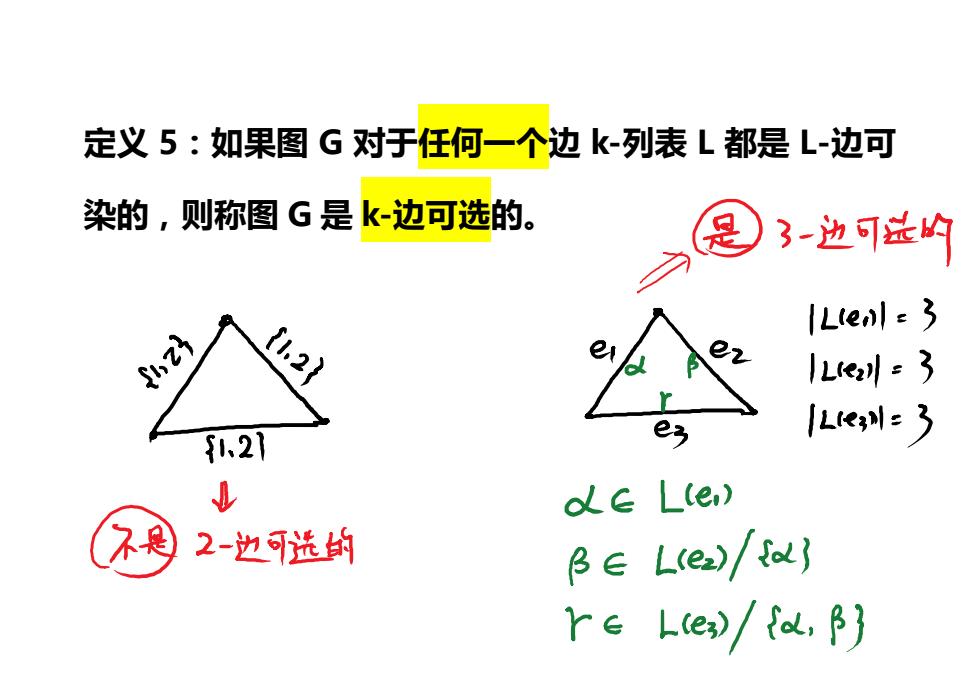
定义5:如果图G对于任何一个边k-列表L都是L-边可 染的,则称图G是k-边可选的。 3-边可益4 Ltenl 3 11.2} L=3 e IL3 1、21 olE Lle) 2-边可选的 BE L(ez)/to Y∈Le/fa,)
定义 5:如果图 G 对于任何一个边 k-列表 L 都是 L-边可 染的,则称图 G 是 k-边可选的

定义6:使得图G是k-边可选的最小整数k是图的列表 边色数,记为1ist(G) 列表边染色猜想 。 I'list (G)=(G) 很难!!!它对于完全图,竟然还没有解决!
定义 6:使得图 G 是 k-边可选的最小整数 k 是图的列表 边色数,记为 ' (G) list 列表边染色猜想: ' (G) '(G) list 很难!!!!!它对于完全图,竟然还没有解决!!!

完全图Kn: 有个顶点,并且任何两个点之间都有一条边的图。 Ka n是偶敏
完全图 Kn: 有 n 个顶点,并且任何两个点之间都有一条边的图
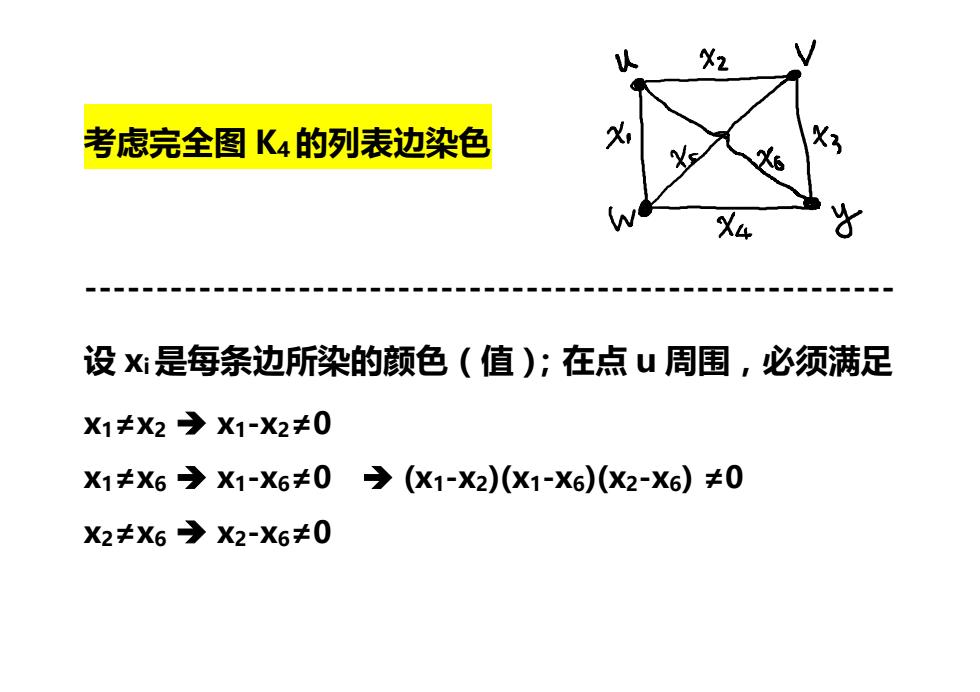
考虑完全图K4的列表边染色 X X3 4 设X是每条边所染的颜色(值);在点山周围,必须满足 X1≠X2)X1-X2≠0 X1≠X6)X1-X6≠0 →(X1-X2)(X1-X6)(x2-X6)≠0 X2≠X6→X2-X6≠0
考虑完全图 K4的列表边染色 --------------------------------------------------------- 设 xi是每条边所染的颜色(值);在点 u 周围,必须满足 x1≠x2 x1-x2≠0 x1≠x6 x1-x6≠0 (x1-x2)(x1-x6)(x2-x6) ≠0 x2≠x6 x2-x6≠0

X2 考虑完全图K4的列表边染色 X3 X4 在点V周围,必须满足 X2≠X3)X2-X3≠0 X2≠X5)X2-X5≠0 →(X2-3)(X2-X5)(X3-X5)≠0 X3≠X5)X3-X5≠0
考虑完全图 K4的列表边染色 --------------------------------------------------------- 在点 v 周围,必须满足 x2≠x3 x2-x3≠0 x2≠x5 x2-x5≠0 (x2-x3)(x2-x5)(x3-x5) ≠0 x3≠x5 x3-x5≠0