
西安毛子科技大学数学与统计学院XIDIAN UNIVERSITYSchool of mathenmnties and sttisties西等数学第一节微分中值定理
第一节 微分中值定理
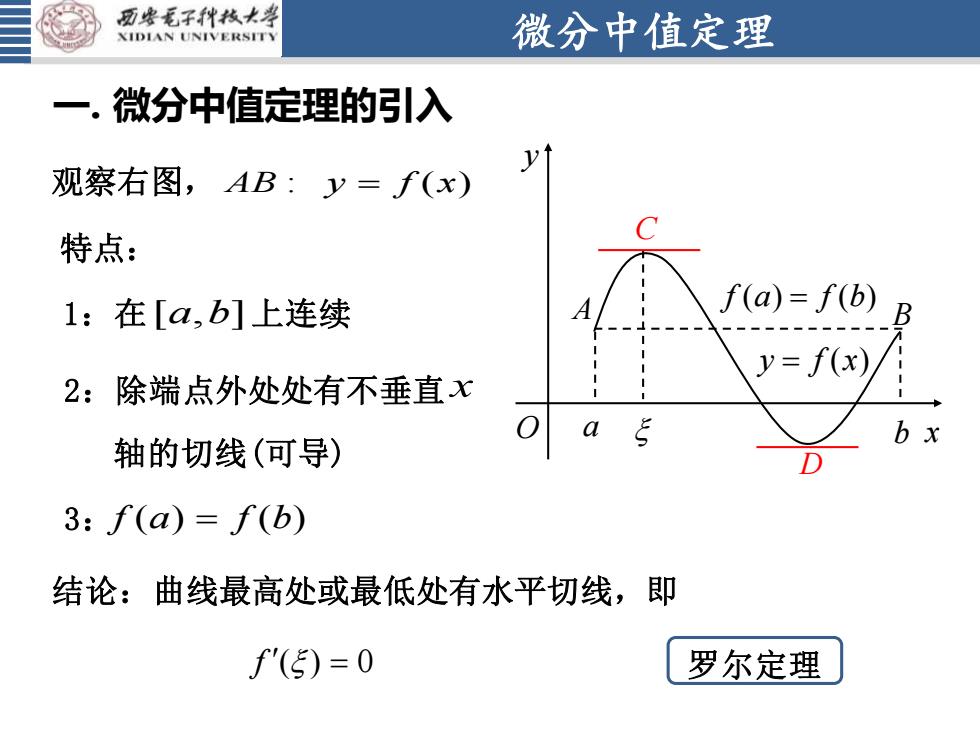
西安毛子科技大学微分中值定理XIDIAN UNIVERSITY一.微分中值定理的引入y观察右图,AB:=f(x)特点:f(a)= f(b)1:在[a,b]上连续y= f(x)2:除端点外处处有不垂直X0a5bx轴的切线(可导)D3: f(a) = f(b)结论:曲线最高处或最低处有水平切线,即f'() = 0罗尔定理
微分中值定理 一. 微分中值定理的引入 f a f b ( ) ( ) = B y f x = ( ) A a b x yO C D 特点: 观察右图, AB y f x : ( ) = 1:在 [ , ] a b 上连续 2:除端点外处处有不垂直 x 3: f a f b ( ) ( ) = 结论:曲线最高处或最低处有水平切线,即 f ( ) 0 = 罗尔定理 轴的切线(可导)

西安毛子科技大学微分中值定理IDIAN UNIVERSITY费马(fermat)引理引理设 f(x)在 xo的某个邻域U(xo)内有定义且在Xo处可导,若对任意 x EU(xo),有f(x)≤ f(xo)(f(x)≥ f(xo)则f(x) = 0证不妨设 VxeU(xo)时,f(x)≤ f(xo), (0 + Ax)- f(x0) = f(x0)lim AxAx->0当 Ax>0 时, I(+)-() ≤0→ J(%)≤0△xf'(x)= 0当 Ax<0 时, F(o +An)-() ≥0 = f()≥0△x
微分中值定理 费马(fermat)引理 引理 设 f x( ) 在 x0 的某个邻域 U( ) x0 内有定义 且在 x0 处可导,若对任意 x x U( ), 0 有 0 0 f x f x f x f x ( ) ( ) ( ( ) ( )) 则 0 f x ( ) 0 = 0 f x f x ( ) ( ) , 0 0 ( ) ( ) 0 f x x f x x + − 0 f x + ( ) 0 0 f x -( ) 0 0 0 0 0 ( ) ( ) lim ( ) x f x x f x f x → x + − = 0 证 不妨设 x x U( )0 时, 当 x 0 时, 0 0 f x x f x ( ) ( ) x + − 当 x 0 时, 0 = f x ( ) 0

西安毛子科技大学微分中值定理XIDIAN UNIVERSITY二.罗尔定理定理1 (罗尔定理)如果函数f(x)满足(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3) f(a)= f(b),则在 (a,b)内至少存在一点≤,使得 f()=0证由于f(x)在[a,b]上连续,f(x)在[a,b]上一定取得最大值M和最小值m
微分中值定理 定理1 (罗尔定理) 二. 罗尔定理 (1) 在闭区间 a b, 上连续; (2) 在开区间 ( , ) a b 内可导; (3) f a f b ( ) ( ), = 证 由于 f x( ) 在 a b, 上连续, f x( ) 在 a b, 上一定取得最 大值 M 和最小值 m. 则在 ( , ) a b 内至少存在一点 ,使得 f ( ) 0. = 如果函数 f x( ) 满足

西安毛子科技大学微分中值定理XIDIANUNIVERSIT(1)如果 M=m,则 f(x)=M(常数),因此任取 E(a,b),都有 f()=0,结论成立.(2)如果 M ± m,则 M 和m至少有一个不等于f(a)和f(b),不妨设 M ≠ f(a), 这时 M ≠ f(b)则存在 三E(a,b), 使得 f()= M即对 VxE[a,b],有 f(x)≤f()由费马引理知:f'()=0
微分中值定理 则存在 ( , ), a b 使得 f M ( ) . = (1) 如果 M m= , 都有 f ( ) 0, = 结论成立. (2) 如果 M m , 由费马引理知: f ( ) 0. = 则 f x M ( ) (常数),因此任取 ( , ) a b , 则 M 和 m 至少有一个不等于 f a( ) 和 f b( ), 不妨设 M f a ( ), 这时 M f b ( ). 即对 x a b [ , ], 有 f x f ( ) ( ).
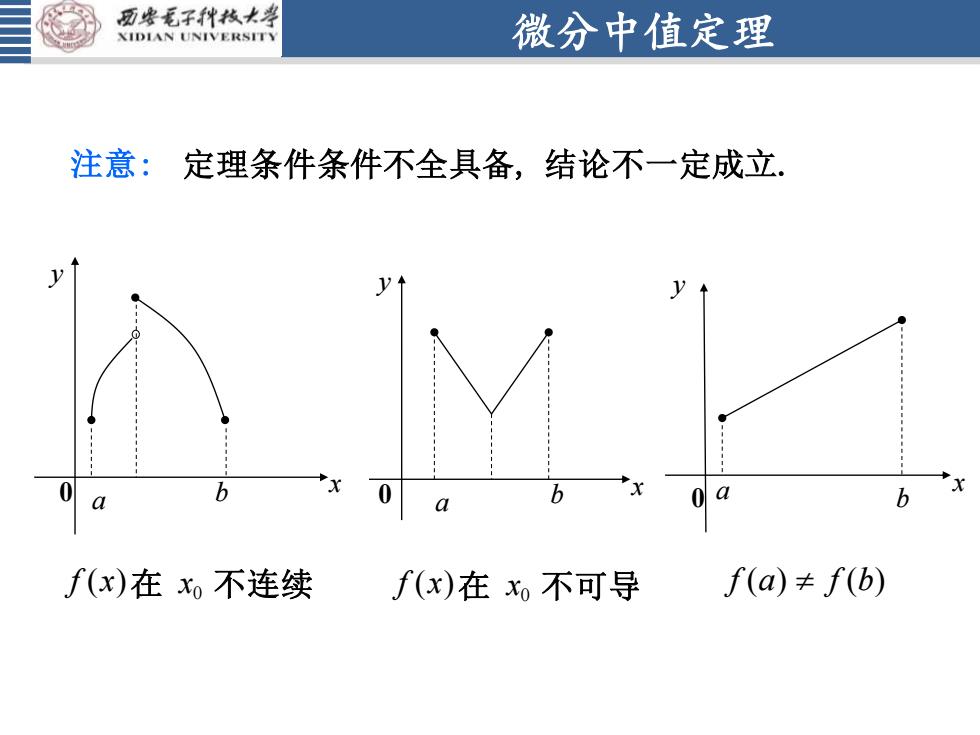
西安毛子科技大学微分中值定理XIDIANUNIVERSITY注意:定理条件条件不全具备,结论不一定成立LVb00boabaf(a) # f(b)f(x)在 xo 不连续f(x)在 xo不可导
微分中值定理 注意: 定理条件条件不全具备, 结论不一定成立. x y 0 a 0 x b x y 0 a b 0 x a b x y 0 f x( ) 在 x0 不连续 f a f b ( ) ( ) f x( ) 在 x0 不可导

西要毛子科技大学微分中值定理XIDIANUNIVERSIT例1证明方程xs+x-1=0只有一个正根证(存在性)设f(x)=xs +x-1,则f(x)在[0,1]上连续f(1) =1.且,f(0)=-1,由零点定理可知:存在 xE(0,1),使得 f(x)=0即f(x)=0 在(0,+) 内至少有一根
微分中值定理 且 f (0) 1, = − f (1) 1. = 例1 证明方程 只有一个正根. 5 x x + − =1 0 由零点定理可知:存在 x0 (0,1) ,使得 0 f x( ) 0, = 即 f x( ) 0 = 在 (0, ) + 内至少有一根. 证(存在性) 设 则 在 上连续, 5 f x x x ( ) 1, = + − f x( ) [0,1]

西安毛子科技大学微分中值定理XIDIAN UNIVERSITS例1证明方程x+x-1=0只有一个正根证(唯一性)假设另有x E(O,+oo)使 f(x)=f(x)=0因为f(x)在以xo,x为端点的区间满足罗尔定理条件所以在xo,x之间至少存在一点,使f()=0又f(x)=5x4+1>0,矛盾,故假设不真。综上xs+x-1=0只有一个正根
微分中值定理 例1 证明方程 只有一个正根. 5 x x + − =1 0 故假设不真. 因为 f x( ) 在以 x0 , x1 为端点的区间满足罗尔定理条件, 又 矛盾, 4 f x x ( ) 5 1 0, = + 综上 只有一个正根. 5 x x + − =1 0 所以在 x0 , x1 之间至少存在一点 , 使 f ( ) 0, = 证(唯一性) 假设另有 x1 + (0, ) 使 1 0 f x f x ( ) ( ) 0, = =
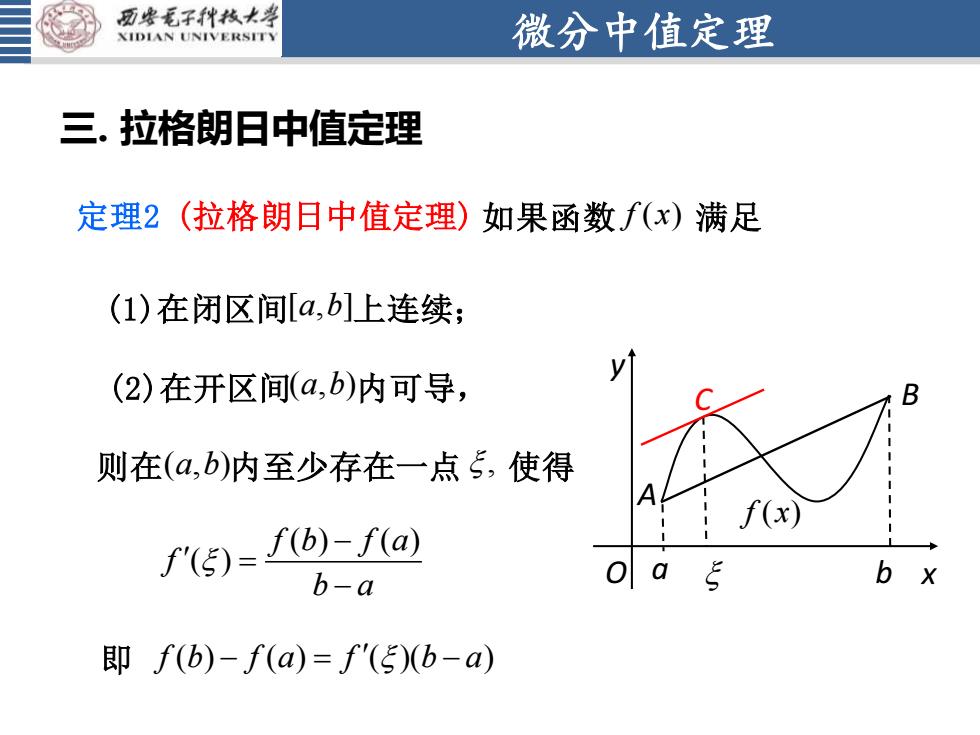
西安毛子科技大学微分中值定理IDIAN UNIVERSITY三.拉格朗日中值定理定理2(拉格朗日中值定理)如果函数f(x)满足(1)在闭区间[a,b]上连续;y(2)在开区间(a,b)内可导,则在(a,b)内至少存在一点,使得fx(s)= (b)-f(a)0a5b+b-a即 f(b)-f(a)=f'()(b-a)
微分中值定理 三. 拉格朗日中值定理 (1)在闭区间 [ , ] a b 上连续; (2)在开区间 ( , ) a b 内可导, 则在 ( , ) a b 内至少存在一点 , 使得 ( ) ( ) ( ) f b f a f b a − = − A B a b x y O C f x( ) 定理2 (拉格朗日中值定理) 如果函数 f x( ) 满足 即 f b f a f b a ( ) ( ) ( )( ) − = −

西安毛子科技大学微分中值定理XIDIAN UNIVERSITY证构造一个辅助函数 0(x)=f(x)-(b)-(a)xb-a由于β(x)在[a,b]上连续,在(a,b)内可导.又(a) = bf(a)-af(b)= p(b)b-a故β(x)在[a,b上满足罗尔定理的条件;因此至少存在一点 ε(a,b), 使得 β'()=0,f(b)-f(a)即= f'(E)b-a
微分中值定理 证 由于 ( ) x 在 [ , ] a b 上连续,在 ( , ) a b 内可导. 又 ( ) ( ) ( ) b f a a f b a b a − = − ( ) ( ) ( ) ( ) , f b f a x f x x b a − = − − 构造一个辅助函数 使得 ( ) 0, = 故 ( ) x 在 [ , ] a b 上满足罗尔定理的条件, 因此至少存在一点 ( , ), a b=( ) b ( ) ( ) ( ) f b f a f b a − = − 即