
西安毛子科技大学数学与统计学院Schoolofmathematies andstatisticsXIDIAN UNIVERSITY畜等数学第四节无穷小与无穷大
第四节 无穷小与无穷大

西要毛子科技大学无穷大与无穷小XIDIAN UNIVERSITY一、无穷小定义1若lim f(x)=0(limf(x)=0),则称函数f(x)为 x→x(x→8)时的无穷小例如 lim(x-1)=0,函数x-1为当 x→1时的无穷小;t-lim==0,函数=为当x→αo时的无穷小。X>00Xx
无穷大与无穷小 一、无穷小 定义1 则称函数 为 时的无穷小. 例如 函数 为当 时的无穷小; (lim ( ) 0 , x f x → = ) 函数 为当 时的无穷小. 1 lim 0 x→ x = , ( ) x →

西安毛子科技大学无穷大与无穷小XIDIAN UNIVERSITY注极限为零的变量称为无穷小1.无穷小是变量,不能与很小的数混淆;2.零是唯一可以作为无穷小的常数;3.函数是否为无穷小,与自变量的变化趋势有关例如 lim(x-1)=0,函数x-1为当 x→1时的无穷小;lim e=0,函数e为当x→-o 时的无穷小。x→-
无穷大与无穷小 注 1. 无穷小是变量,不能与很小的数混淆; 2. 零是唯一可以作为无穷小的常数; 3. 函数是否为无穷小,与自变量的变化趋势有关. 极限为零的变量称为无穷小 例如 函数 为当 时的无穷小; lim e 0 x x→ − = , 函数 为当 时的无穷小.

西安毛子科技大学无穷大与无穷小XIDIANUNIVERSITY定理1 lim f(x)= A f(x)= A+α(x),其中α(x)是当x→x时的无穷小。证limf(x)=A>0, 8>0,当0<|x-x。<时,1f(α)-A<8.令α(x)= f(x)-A, f(x)=A+α(x) 且limα(x)=0.x→X0
无穷大与无穷小 定理1 0 lim ( ) ( ) ( ), x x f x A f x A x → = = + 当 → x x0 时的无穷小. 其中 ( ) x 是 证 令 = − ( ) ( ) x f x A, 0 lim ( ) 0, x x f x A → = 0, 0 ( ) ( ) lim ( ) 0 x x f x A x x → = + = 且 .

西安毛子科技大学无穷大与无穷小XIDIAN UNIVERSITY二、无穷大定义2 设函数f(x)在点 xo的某一去心邻域内有定义,若M>0,38>0,当0M,则称f(x)为当 x→x时的无穷大.记作 lim f(x)=o0lim f(x)=00 VM>0, 3X>0,X-00M-X定义当Ix|>X时,有/f(x)|>M.注函数极限为无穷大,它的极限不存在
无穷大与无穷小 二、无穷大 定义2 设函数 在点 的某一去心邻域内有定义, 若 M 0, 为 0, f x( ) 当 时的无穷大. 0 lim ( ) x x f x → 记作 = 则称 注 函数极限为无穷大,它的极限不存在. M 0, 0, 0 lim ( ) x x f x → = M − 定义 X 0, | | x X X

西安毛子科技大学无穷大与无穷小XIDIANUNIVERSITS1.可类似给出正无穷大和负无穷大的定义:2.函数极限为(正、负)无穷大,它的极限不存在;3.无穷大是变量,不能与很大的数混淆,lim f(x)=+00≤ VM >0,38>0,M-8定义当0M
无穷大与无穷小 M 0, 0, 0 lim ( ) x x f x → = M − 定义 1. 可类似给出正无穷大和负无穷大的定义; f x M ( ) . + 2. 函数极限为(正、负)无穷大,它的极限不存在; 3. 无穷大是变量,不能与很大的数混淆.

西安毛子科技大学无穷大与无穷小XIDIAN UNIVERSITY1例1证明lim8x-2 x - 2证 VM>0,要使M,0Xx1只要「x-取8当0<|x-2|<8时,MM1有M.因此 lim8x-2 x - 2X1注直线x=2是函数y=的图形的铅直渐近线x-2
无穷大与无穷小 例1 证明 证 要使 只要 取 因此 2 1 lim x→ x 2 = − . 1 2 M x − , 1 | 2 | x M − , 2 1 lim x→ x 2 = − . M 0, 有 o x y 1 2 y x = − 2 1 M = , 1 2 M x − . 注 直线 x = 2 是函数 的图形的铅直渐近线
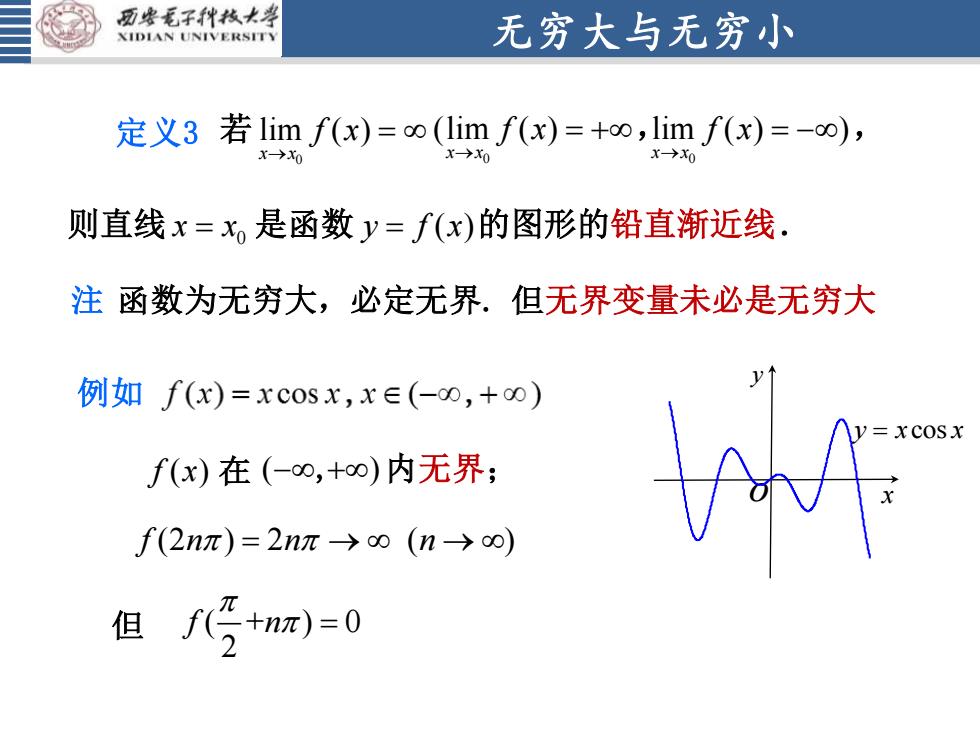
西安毛子科技大学无穷大与无穷小XIDIANUNIVERSITY定义3 若 lim f(x)= oo (lim f(x)=+o0,lim f(x)=-o),则直线x=x是函数y=f(x)的图形的铅直渐近线注函数为无穷大,必定无界.但无界变量未必是无穷大例如 f(α)=xcos x, x E(-o0,+o0)cosxf(x)在(-0,+oo)内无界;f(2n元)=2n元 → 0 (n →0)f(+n元)=0但
无穷大与无穷小 定义3 0 lim ( ) x x f x → 若 = 0 则直线 = = x x y f x 是函数 ( )的图形的铅直渐近线. 0 0 (lim ( ) lim ( ) ) x x x x f x f x → → = + = − , , 注 函数为无穷大,必定无界. 但无界变量未必是无穷大 例如 f x( ) 在 ( ) − + , 内无界; o x y y x x = cos f n n n (2 ) 2 ( ) = → → 但 ( + ) 0 2 f n =

西安毛子科技大学无穷大与无穷小XIDIAN UNIVERSITY定理2 在自变量的同一变化过程中,若f(α)为无穷大1则为无穷小;反之若f(x)为无穷小,且f(x)≠0,f(x则 ()为无穷大
无穷大与无穷小 定理2 在自变量的同一变化过程中,若 为无穷大, 1 f x( ) 则 为无穷小;反之若 为无穷小,且 f x( ) 0 , 则 为无穷大. 1 f x( )

西安毛子科技大学无穷大与无穷小IDIANUNIVERSITY三、无穷小的运算法则定理3两个无穷小的和(差)是无穷小。证设limα=0,limβ=0,→XoX→XoC>0, >0,当00,当<x-<,时,有β号2取 8=min[8,8,},则当0<|x-xl<8 时,有[α-β≤α]+Iβ+=8,因此 lim(α-β)=0.2'2→X
无穷大与无穷小 三、无穷小的运算法则 定理3 两个无穷小的和(差)是无穷小. = min{ } 1 2 , , 时, 证 设 取 则当 0 0 | | − x x 0 lim 0 x x → = , 0 lim 0 x x → = , 0, 当 时,有 当 时,有 0 1 0 | | − x x 0 2 0 | | − x x | | | | | | + + 2 2 有 + = , 因此 0 lim ( ) 0 x x → − −+ = .