
行列式的计算方法小结

HH1、定义法:适用于0比较多的行列式2、利用性质化三角形行列式3、按行(列)展开4、其他方法:福析因子法箭形行列式行(列)和相等的行列式递推公式法HHHHHHHH加边法(升级法)拆项法数学归纳法衍列式的计算下页返回上页
行列式的计算 4、 其他方法: 1、定义法:适用于0比较多的行列式. 2、利用性质化三角形行列式 3、 按行(列)展开 析因子法 箭形行列式 行(列)和相等的行列式 递推公式法 加边法(升级法) 拆项法 数学归纳法

HH(一)析因子法1231-x?3221例:计算D=522319-x231解:由行列式D定义知为x的4次多项式。又,当x=±1时,1,2行相同,有D=0,:.x=±1 为D的根,当x=±2 时,3,4行相同,有 D=0,..x=±2为D的根。一故D有4个一次因式:x+1,x-1,x+2,x-2工行列式的计算上页返回下页
行列式的计算 (一)析因子法 2 2 1 1 2 3 1 2 2 3 2 3 1 5 2 3 1 9 x D x − = − 例:计算 解:由行列式 D 定义知为 x 的4次多项式. 又,当 x = 1 时,1,2行相同,有 D = 0 , = x 1 为D的根. 当 x = 2 时,3,4行相同,有 D = 0, = x 2 为D的根. 故 D 有4个一次因式: x x x x + − + − 1, 1, 2, 2

HHHHHH设 D = a(x + 1)(x - 1)(x + 2)(x - 2),31213221D== -12令x=0,则3519即,a·1·(-1)·2·(-2) = -12. :. a = -3..: D = -3(x + 1)(x - 1)(x + 2)(x - 2)HHHHHHH衍列式的计算下页返回上页
行列式的计算 设 D a x x x x = + − + − ( 1)( 1)( 2)( 2), 令 x = 0, 则 1 1 2 3 1 2 2 3 12 2 3 1 5 2 3 1 9 D = = − 即, a − − = − 1 ( 1) 2 ( 2) 12. = − a 3. = − + − + − D x x x x 3( 1)( 1)( 2)( 2)

HH箭形行列式(二)广广Eaob.bb.c1a一Dn+1Sa, +0,i =1,2,3...n.=?.cnanC解:把所有的第i+1列(i=l,.…,n)的 倍加到Iai第1列,得:HHHHHHHD.-4.-.(.--)行列式的计算上页回
行列式的计算 (二)箭形行列式 0 1 2 1 1 1 2 2 , 0, 1,2,3 . n n i n n a b b b c a D a i n c a c a + = = 解:把所有的第 列 ( 1, , ) i n = 的 倍加到 i i c a − i + 1 第1列,得: 1 1 2 0 1 ( ) n i i n n i i b c D a a a a a + = = −

T可转为箭形行列式的行列式:11+ a.1111+az1)a, 0,i = 1,2,3...n.91......1......1+anxa..xxxaz..2)a, + 0,i = 1,2,3...n.9xxan一十1(把第i行分别减去第1行,即可转为箭形行列式)十工HHH衍列式的计算返回上页下页
行列式的计算 可转为箭形行列式的行列式: 1 2 1 1 1 1 1 1 1) , 0, 1,2,3 . 1 1 1 i n a a a i n a + + = + 1 2) , 0, 1,2,3 . 2 i n a x x x a x a i n x x a = (把第 i 行分别减去第1行, 即可转为箭形行列式)

HH(三)行(列)和相等的行列式HHHHHHHbab6T11)D二.5aba+(n-1)b b...解:Dba+(n-1)ba...c +c +...+c.::..第a+(n-1)b b ...ab1 b6a=(a + (n- 1)b)::7a5b0r-r=(a-b)"-l(a+(n-1)b(a+(n-1)b)..i=2.3....n00a-b...HHH行列式的计算上页返回下质
行列式的计算 (三)行(列)和相等的行列式 1) a b b b a b D b a = 1 2 ( 1) ( 1) ( 1) n a n b b b a n b a b c c c a n b b a + − + − + + + + − 解: D ( ) 1 1 ( 1) 1 b b a b a n b b a = + − ( ) 1 1 0 0 ( 1) 2,3, 0 0 i b b r r a b a n b i n a b − − + − = − ( ) 1 ( ) ( 1) n a b a n b − = − + −
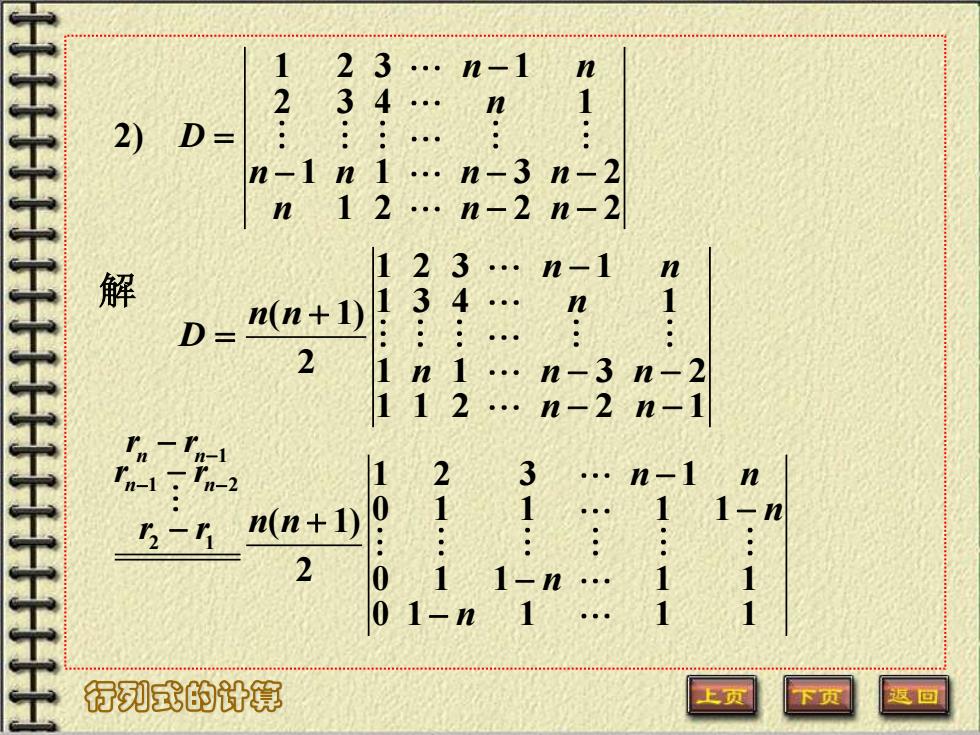
HHHHHHHHH123nn2.:31::4n.......2)D=237n一n-Sn-221n-2...nn-2n-in.解314nn(n + 1)..D=23nn一n-122n-1...n-1n-2I3n011n(n+ 1)HHHHHHH......121·.....2101n1110 1-n行列式的计算上页下页返回
行列式的计算 1 2 3 1 2 3 4 1 2) 1 1 3 2 1 2 2 2 n n n D n n n n n n n − = − − − − − 1 2 3 1 1 3 4 1 ( 1) 2 1 1 3 2 1 1 2 2 1 n n n n n D n n n n n − + = − − − − 解 1 1 2 2 1 1 2 3 1 0 1 1 1 1 ( 1) 2 0 1 1 1 1 0 1 1 1 1 n n n n r r r r r r n n n n n n n − − − − − − − − + − −

H1I-n...n(n+ 1)广一12广E1-nHHHn-111..-nn(n+ 1)00r -rnn2i=2,3..n-1-00-nnn-山1n(n + 1)000工2...Ch-+ +c+ +.+cn-2000-n一n-1HHHHH(n-1)(n-1)(n-" (n + 1)n-ln(n+ 1)(-1)(-n)"-2 =(-1) 22-1)22行列式的计算上页返回下页二
行列式的计算 1 1 1 1 1 ( 1) 2 1 1 1 1 1 1 1 1 n n n n n n − − + = − − 1 1 1 1 1 1 ( 1) 0 0 2,3 1 2 0 0 i n n r r n n n n i n n n − − − + − = − − 1 1 2 1 1 1 1 1 ( 1) 0 0 0 2 0 0 0 n n n n n n c c c n − − − − + − + + + − ( 1)( 1) 2 2 ( 1)( 1) ( 1)( ) 2 n n n n n n − − + − = − − − ( 1) 1 2 ( 1) ( 1) 2 n n n n n − − + = −

HHHHHHHHH(四)升级法(加边法)a, + b,a2ara, + b,·anD, =b,b, ...b, +0.a, +b.aia2解:HHHHHHHHHHHH1aan.0a +b101)D =02福e...0a, +b.a,nIn+1衍列式的计算下页返回上页
行列式的计算 (四)升级法(加边法) 1 1 2 1 2 2 1 2 1 2 , 0 n n n n n n a b a a a a b a D b b b a a a b + + = + 1 2 1 1 2 1 2 2 1 2 1 1 0 0 0 n n n n n n n a a a a b a a D a a b a a a a b + + = + + 解: 1)