西安电子科技大学：《高等数学》课程PPT教学课件（讲稿）第二章 导数与微分 2.2 函数的求导法则

西安毛子科技大学数学与统计学院XIDIAN UNIVERSITYSchool ofmathenmntics and stntisties西等数学第二节函数的求导法则

第二节 函数的求导法则

西安毛子科技大学函数的求导法则XIDIAN UNIVERSITY函数的和、差、积、商的求导法则定理1 如果函数f(x)及g(x)都在点x 可导，那么它们的和、差、积、商（分母不为零）都在点x可导，且(1) [f(x)±g(x)}'= f'(x)±g(x);(2) [f(x)·g(x)}'= f'(x)g(x)+ f(x)g'(x);f(x)f(x)g(x)- f(x)g(x)(3)(g(x) ± 0).g (x)g(x)

函数的求导法则 一、 函数的和、差、积、商的求导法则 定理1 如果函数 f x( ) 及 g x( ) 都在点 x 可导，那么它们的和、 差、积、商(分母不为零）都在点 x 可导，且 （1） [ ( ) ( )] ( ) ( ); f x g x f x g x  =     （2） [ ( ) ( )] ( ) ( ) ( ) ( ); f x g x f x g x f x g x  = +    2 ( ) ( ) ( ) ( ) ( ) ( ( ) 0). ( ) ( ) f x f x g x f x g x g x g x g x      − =      （3）

西安毛子科技大学函数的求导法则XIDIANUNIVERSITY证仅对乘积形式的求导公式给出证明[(x) g(x)= lim (x+Ax)g(x+Ar)-(x)g()AxAx->0f(x +△x)g(x+△x)- f(x)g(x+Ax)+ f(x)g(x+△x)- f(x)g(x)= limArAx->0F(x+Ar)-f() im g(x+ Ax)+ f(x) im g(x +△x)- g(x):limAr→>0AxAxAr->0Ax故公式成立= f'(x)g(x)+ f(x)g'(x)

函数的求导法则 证 仅对乘积形式的求导公式给出证明 [ ( ) ( )] f x g x   0 ( ) ( ) ( ) ( ) lim x f x x g x x f x g x  → x +  +  − =  0 ( ) ( ) ( ) ( ) lim ( ) ( ) ( ) ( ) x f x x g x x f x g f x g x x f x x g x x x  →   +  +  − − +  =     +   + 0 0 0 ( ) ( ) ( ) ( ) lim lim ( ) ( ) lim x x x f x x f x g x x g x g x x f x  →  →  → x x +  − +  − =  +  +    = + f x g x f x g x   ( ) ( ) ( ) ( ). 故公式成立

西安毛子科技大学函数的求导法则XIDIAN UNIVERSITY注 1公式（1）（2）可以推广到有限个可导函数的情形，如[f(x)+g(x)+h(x))'= f'(x)+g'(x)+h'(x)[f(x)·g(x). h(x))' = f'(x)g(x)h(x)+ f(x)g'(x)h(x)+ f(x)g(x)h(x2 公式（2）中取g(x)=C,可得[C·f(x)}=C·f(x)

函数的求导法则 注 1 [ ( )+ ( ) ( )] ( ) ( ) ( ) f x g x h x f x g x h x + = + +     [ ( ) ( ) ( )] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) f x g x h x f x g x h x f x g x h x f x g x h x   = + +     公式（1）（2）可以推广到有限个可导函数的情形，如 2 公式（2）中取 g x C ( ) , = 可得 [ ( )] ( ) C f x C f x  =   

西要毛子科技大学函数的求导法则XIDIANUNIVERSITY例1 设 f(x)=log。x,其中 a>0,a≠l, 求f(x)Inx解由换底公式 f(x)Ina1111in(lnx)"故f'(x)=InaxlnaInaxIna(loga x)即xlna

函数的求导法则 解 即 ( ) 1 log ln a x x a  = 例1 设 ( ) log , 求 f x ( ). a f x x = 其中 a a   0, 1, ln ( ) ln x f x a 由换底公式 = 故 ln ln x a    =     1 (ln ) ln x a =  1 1 ln a x = 

西安毛子科技大学函数的求导法则XIDIAN UNIVERSITY例2 求证(tanx)= sec2 x，(cscx)'=-cscxcotx,(sin x)'cos x -sin x(cosx)sin x证(tan x)':COSxcos? xcos? x +sin? x= Sec2 xcos?x-(sin x)-coS xcscxsin xsin? xsin? x=-cscxcot x类似可证：(cot x)'=-csc2 x，(secx)'= secxtan x

函数的求导法则 (csc ) x  = 1 sin x        2 sin x = −(sin ) x  2 sin x = 例2 求证 证 sin (tan ) cos x x x     =     = 2 cos x (sin ) cos x x  −sin (cos ) x x  = 2 cos x 2 cos x 2 +sin x 2 = sec x−cos x = −csc cot x x 类似可证: 2 (cot ) csc , x x  = − (sec ) sec tan . x x x  =

西安毛子科技大学函数的求导法则XIDIANUNIVERSIT二、 反函数的求导法则定理2如果函数x=f(y)在区间I,内单调可导且f(y)±0;则其反函数 y=f-(x)在 I,=(x|x=f(y),eI,) 内可导1dy.1反函数的且[f-1(x)}":或dxdxf'(y)导数等于dy证原函数导Ay111数的倒数lim[f-'(x)}'= limlimAxAy->0 AxAr->0f'(y)Ar-0 △xAyAyy=f-(x）单调y=f-(x)在I连续=Ay=f-(x+Ax)-f-(Ax)±0

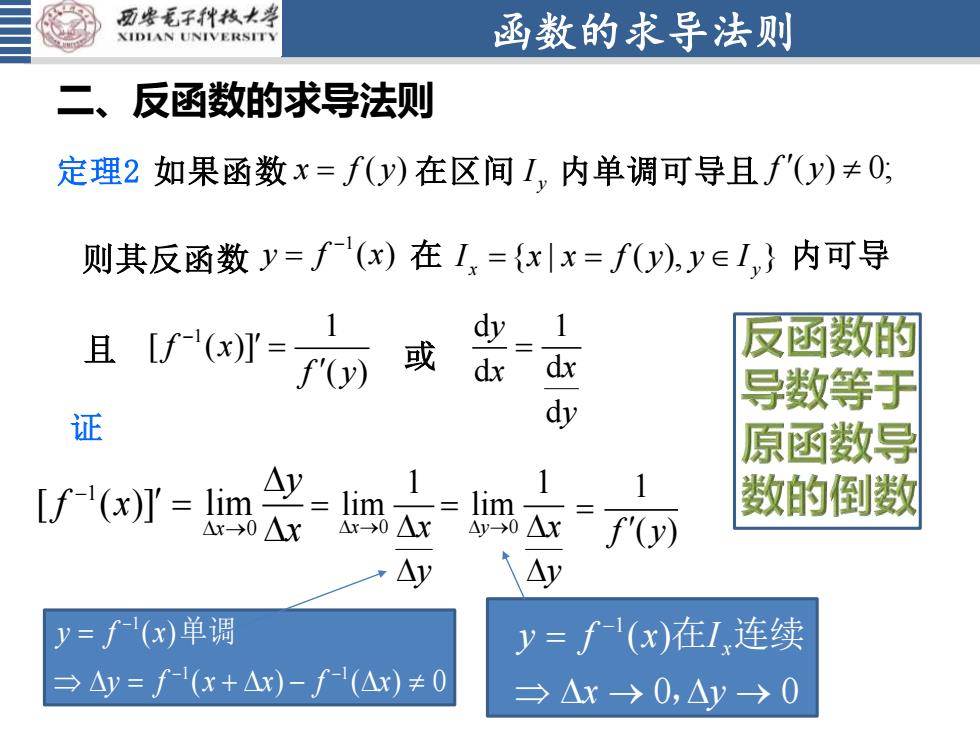
函数的求导法则 二、反函数的求导法则 或 定理2 如果函数 x f y = ( ) 在区间 I y 内单调可导且 f y ( ) 0;  1 1 [ ( )] ( ) f x f y −  =  1 y f x( ) − 则其反函数 = 在 I x x f y y I x y = =  { | ( ), } 内可导 且 d 1 d d d y x x y = 证 1 0 [ ( )] lim x y f x x −  →   =  0 1 lim x x y  → =   1 1 1 ( ) ( ) ( ) 0 y f x y f x x f x − − − =   = +  −   单调 1( ) 0 0 y f x I x x y − =   →  → 在 连续 ， 0 1 lim y x y  → =   1 f y( ) = 

西安毛子科技大学函数的求导法则XIDIAN UNIVERSITS例3求y=arcsinx(-1O2'2故y=arcsin x在（-1,1)可导，且1111(arcsin x)(sin y)cos yV1-x?V1-sin?--1(arccos x)"类似可得V1- x211(arctan x)'(arccot x)'1+x21 + x2

函数的求导法则 解 y x = arcsin 是 x y = sin 的反函数 例3 求 y x x = −   arcsin ( 1 1) 的导数. 而 x y = sin 在 ( , ) 2 2   − 内单调，可导且 (sin ) cos 0 y y  =  故 y x = arcsin 在 ( 1,1) − 可导，且 1 (arcsin ) (sin ) x y  =  1 cos y = 2 1 1 sin y = − 2 1 1 x = − 2 2 2 1 (arccos ) 1 1 1 (arctan ) , (arccot ) . 1 1 x x x x x x −  = − −   = = + + 类似可得

西安毛子科技大学函数的求导法则XIDIANUNIVERSITY例4设y=α，其中α>0,al，求y解由于 x=loga在(O,+oo)内单调可导，且则[loga y]' =± 0, yE(0,+);ylnay=α在（-o0,+o)内可导，且y'=(a') =ylna =a'Ina.(a")'= a" Ina即(e*)'=er特别地

函数的求导法则 解 由于 loga x y = 在 (0, ) + 内单调可导，且 1 [log ] 0, (0, ); ln a y y y a  =   + 则 x y a = 在 ( , ) − + 内可导，且 ( )x y a   = 即 ( ) ln x x a a a  = = y a ln ln . x = a a 例4 设 , x y a = 其中 a a   0, 1, 求 y  . 特别地 (e ) e x x  =

西安毛子科技大学函数的求导法则XIDIAN UNIVERSITS定理3如果函数u=g(x）在点x可导，而函数y=f(u)在点u=g(x)可导，则复合函数y=f[g(x)) 在点 x可导，且其导数为dy dy dudy f(u)·g'(x)或dxdu dxdxuxVddu复合函数求导的链式法则dudx即因变量对自变量求导,等于因变量对中间变量求导，乘以中间变量对自变量求导

函数的求导法则 即 因变量对自变量求导,等于因变量对中间变量求导, 定理3 如果函数 u g x = ( ) 在点 x 可导 而函数 y f u = ( ) 在点 d d d d d d y y u x u x =  d ( ) ( ). d y f u g x x 或 =    y u x → →d ——复合函数求导的链式法则 d u x d d y u 乘以中间变量对自变量求导. u g x = ( ) 可导 则复合函数 y f g x = [ ( )] 在点 x 可导，且其导数为