
《高等数学A(I)》教学大纲课程编号:MS006001课程名称:高等数学A(D)英文名称:AdvancedMathematicsA(I)学分/学时:5/80课程性质:必修适用专业:全校工科专业、部分理科专业建议开设学期:第1学期先修课程:无开课单位:数学与统计学院一、课程的教学目标与任务高等数学是高等学校理工科专业重要的基础理论课,是全校性的公共基础课,对于以信息和电子学科为主的各理工科专业,高等数学在大学本科教育阶段显得尤为重要,有着举足轻重的作用。该课程不但是学习复变函数、概率统计、大学物理等课程的必修课,而且为学习专业课程和进一步扩大数学知识奠定必要的数学基础。通过该课程的教学,一是为学生的后继课程教学提供必需的基础数学知识;二是传授数学思想,培养学生的创新意识,逐步提高学生的数学素养、数学思维能力和应用数学知识解决复杂问题的能力。二、课程具体内容及基本要求高等数学是各专业的基础课,它为后继课程及科学研究提供必要的数学工具。高等数学A(I)主要内容有:函数与极限,导数与微分,中值定理与导数应用,不定积分,定积分及其应用,常微分方程。着重介绍其基本概念,基本理论和基本运算。(一)函数、极限与连续(18学时)内容:函数概念、初等函数,数列极限、函数极限,无穷大与无穷小,极限存在准则、无穷小的比较,函数的连续性、闭区间上连续函数的性质。1.基本要求函数:理解函数概念,掌握函数的表示方法。理解复合函数的概念,了解反函数与隐函数的概念。了解函数的性质:有界性、单调性、奇偶性和周期性。掌握基本初等函数的性质及图形。理解初等函数的概念,了解双曲函数与反双曲函数的概念。会建立简单应用问题中的函数关系式。极限:理解极限的概念,了解极限的ε-N和ε-定义。理解函数左、右极限的概念以
《高等数学 A(I)》教学大纲 课程编号:MS006001 课程名称:高等数学 A(I) 英文名称:Advanced Mathematics A(I) 学分/学时:5/80 课程性质:必修 适用专业:全校工科专业、部分理科专业 建议开设学期:第 1 学期 先修课程:无 开课单位:数学与统计学院 一、课程的教学目标与任务 高等数学是高等学校理工科专业重要的基础理论课,是全校性的公共基础课,对于以 信息和电子学科为主的各理工科专业,高等数学在大学本科教育阶段显得尤为重要,有着 举足轻重的作用。该课程不但是学习复变函数、概率统计、大学物理等课程的必修课,而 且为学习专业课程和进一步扩大数学知识奠定必要的数学基础。 通过该课程的教学,一是为学生的后继课程教学提供必需的基础数学知识;二是传授 数学思想,培养学生的创新意识,逐步提高学生的数学素养、数学思维能力和应用数学知 识解决复杂问题的能力。 二、课程具体内容及基本要求 高等数学是各专业的基础课,它为后继课程及科学研究提供必要的数学工具。高等数学 A(I)主要内容有:函数与极限,导数与微分,中值定理与导数应用,不定积分,定积分及其 应用,常微分方程。着重介绍其基本概念,基本理论和基本运算。 (一)函数、极限与连续(18 学时) 内容:函数概念、初等函数,数列极限、函数极限,无穷大与无穷小,极限存在准则、 无穷小的比较,函数的连续性、闭区间上连续函数的性质。 1.基本要求 函数:理解函数概念,掌握函数的表示方法。理解复合函数的概念,了解反函数与隐函 数的概念。了解函数的性质:有界性、单调性、奇偶性和周期性。掌握基本初等函数的性质 及图形。理解初等函数的概念,了解双曲函数与反双曲函数的概念。会建立简单应用问题中 的函数关系式。 极限:理解极限的概念,了解极限的 − N 和 − 定义。理解函数左、右极限的概念以

及极限存在与左、右极限之间的关系。掌握极限的性质(特别是不等式性质)、四则运算法 则及复合运算法则。掌握极限存在的两个准则:夹逼准则与单调有界准则,掌握两个重要极 限:mn-1与ml+=e及利用其求极限的方法。了解数列的Cauchy收敛原理。理 解无穷小、无穷大、高阶无穷小和等价无穷小的概念,会用等价无穷小求极限。 连续:理解函数在一点连续和在一个区间上连续的概念。了解函数间断点的概念,会判 别间断点的类型。理解基本初等函数和初等函数的连续性,会判定分段函数在分段点的连续 性。了解闭区间上连续函数的性质:最大值最小值定理,介值定理。 2.重点、难点 重点:极限概念,极限的四则运算法则,利用两个重要极限求极限,函数的连续性。 难点:极限的定义,极限存在准则。 3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。 (二)一元函数微分学(24学时) 内容:导数概念及导数公式,复合函数、反函数、隐函数和由参数方程所确定的函数的 求导法则,n阶导数,函数的微分。中值定理,洛必达法则,导数的应用。 1.基本要求 导数与微分:理解导数的概念及几何意义,函数的可导性与连续性之间的关系。会求平 面曲线的切线和法线方程,了解导数作为函数变化率的实际意义,会用导数表达一些物理量。 掌握导数的四则运算法则和复合函数的求导法,掌握基本初等函数的求导公式(会用导数定 义讨论分段函数在分段点的可导性)。了解高阶导数的概念,掌握初等函数一阶、二阶导数 的求法,会求一些简单函数的高阶导数。会求反函数的导数,隐函数和由参数方程所确定的 函数的一阶、二阶导数。会解一些简单实际问题中的相关变化率问题。理解微分的概念,了 解微分的几何意义,掌握微分的四则运算法则和微分形式的不变性。了解微分在近似计算及 误差估计中的应用。 中值定理与导数应用:理解罗尔(Rolle)定理和拉格朗日(Lagrange)中值定理,了解如 何构造辅助函数并利用定理证明相关问题。了解柯西(Cauchy)中值定理。了解泰勒(Taylor) 定理以及用多项式逼近函数的思想。掌握洛必达法则求不定式极限的方法。理解函数的极值 的概念,掌握用导数判断函数的单调性和求极值的方法。会求函数的最大值和最小值及其较 简单的最大值、最小值的应用问题。会用导数判断函数图形的凹凸性,会求拐点,会求水平、 铅直和斜渐近线,会描绘一些简单函数的图形。了解弧微分、曲率和曲率半径的概念,会计 算曲率和曲率半径。 2.重点、难点 重点:导数的定义,初等函数导数的求法(一阶及二阶)。罗尔定理,拉格朗日中值定理
及极限存在与左、右极限之间的关系。掌握极限的性质(特别是不等式性质)、四则运算法 则及复合运算法则。掌握极限存在的两个准则:夹逼准则与单调有界准则,掌握两个重要极 限: 0 sin lim 1 x x → x = 与 1 lim(1 )x x e → x + = 及利用其求极限的方法。了解数列的 Cauchy 收敛原理。理 解无穷小、无穷大、高阶无穷小和等价无穷小的概念,会用等价无穷小求极限。 连续:理解函数在一点连续和在一个区间上连续的概念。了解函数间断点的概念,会判 别间断点的类型。理解基本初等函数和初等函数的连续性,会判定分段函数在分段点的连续 性。了解闭区间上连续函数的性质:最大值最小值定理, 介值定理。 2.重点、难点 重点:极限概念,极限的四则运算法则,利用两个重要极限求极限,函数的连续性。 难点:极限的定义,极限存在准则。 3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。 (二)一元函数微分学(24 学时) 内容:导数概念及导数公式,复合函数、反函数、隐函数和由参数方程所确定的函数的 求导法则, n 阶导数,函数的微分。中值定理,洛必达法则,导数的应用。 1.基本要求 导数与微分:理解导数的概念及几何意义,函数的可导性与连续性之间的关系。会求平 面曲线的切线和法线方程,了解导数作为函数变化率的实际意义,会用导数表达一些物理量。 掌握导数的四则运算法则和复合函数的求导法,掌握基本初等函数的求导公式(会用导数定 义讨论分段函数在分段点的可导性)。了解高阶导数的概念,掌握初等函数一阶、二阶导数 的求法,会求一些简单函数的高阶导数。会求反函数的导数,隐函数和由参数方程所确定的 函数的一阶、二阶导数。会解一些简单实际问题中的相关变化率问题。理解微分的概念,了 解微分的几何意义,掌握微分的四则运算法则和微分形式的不变性。了解微分在近似计算及 误差估计中的应用。 中值定理与导数应用:理解罗尔(Rolle)定理和拉格朗日(Lagrange)中值定理,了解如 何构造辅助函数并利用定理证明相关问题。了解柯西(Cauchy)中值定理。了解泰勒(Taylor) 定理以及用多项式逼近函数的思想。掌握洛必达法则求不定式极限的方法。理解函数的极值 的概念,掌握用导数判断函数的单调性和求极值的方法。会求函数的最大值和最小值及其较 简单的最大值、最小值的应用问题。会用导数判断函数图形的凹凸性,会求拐点,会求水平、 铅直和斜渐近线,会描绘一些简单函数的图形。了解弧微分、曲率和曲率半径的概念,会计 算曲率和曲率半径。 2.重点、难点 重点:导数的定义,初等函数导数的求法(一阶及二阶)。罗尔定理,拉格朗日中值定理

洛必达法则,用导数判断函数的单调性及极值。难点:复合函数求导法,高阶导数的求法。泰勒中值定理。3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。(三)一元函数积分学(28学时)内容:不定积分、定积分的概念与性质,换元积分法、分部积分法,牛顿一莱布尼兹公式,广义积分,定积分的应用。1.基本要求不定积分:理解原函数与不定积分的概念,了解不定积分的性质。掌握不定积分的基本公式。掌握不定积分的换元积分法和分部积分法。会求有理函数、三角函数有理式和简单无理函数的积分。定积分:理解定积分的概念和几何意义。理解定积分的性质和定积分中值定理。理解积分上限的函数性质及其求导。掌握牛顿(Newton)一莱布尼兹(Leibniz)公式。掌握定积分的换元积分法和分部积分法。掌握建立定积分表达式的元素法(微元法),会用定积分表达和计算一些几何量和物理量(平面图形的面积、平面曲线的弧长、旋转体的体积、平行截面面积为已知的立体体积、变力作功、引力、压力和函数平均值)。了解广义积分及其收敛性的概念。2.重点、难点重点:不定积分、定积分的换元积分法、分部积分法,积分上限的函数及其求导定理牛顿-莱布尼兹公式。难点:换元积分法,微元法,3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。(四)常微分方程(10学时)内容:微分方程的基本概念,可分离变量的微分方程,齐次方程,一阶线性微分方程特殊类型的二阶微分方程,高阶线性微分方程,,二阶常系数齐次线性微分方程,二阶常系数非齐次线性微分方程。1.基本要求微分方程的基本概念;了解微分方程以及微分方程的解、通解、初始条件和特解的概念一阶微分方程:掌握变量可分离的方程和一阶线性微分方程的解法。会解齐次方程、伯努利方程。会用简单的变量代换求解某些微分方程。二阶微分方程:会用降阶法求解三类方程y()=f(x),y=f(x,y),y"=f(y,y),理解线性微分方程解的性质和解的结构定理。掌握二阶常系数齐次线性微分方程的解法,了解高阶常系数齐次线性微分方程的解法。会求自由项为P,(x)e",e(4cosβx+Bsin βx)的二阶常系数非齐次线性微分方程的特解,其中P,(n)为实系数n次多项式,α,β,A,B为实数。2.重点、难点
洛必达法则,用导数判断函数的单调性及极值。 难点:复合函数求导法,高阶导数的求法。泰勒中值定理。 3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。 (三)一元函数积分学(28 学时) 内容:不定积分、定积分的概念与性质,换元积分法、分部积分法,牛顿—莱布尼兹公 式,广义积分,定积分的应用。 1.基本要求 不定积分:理解原函数与不定积分的概念,了解不定积分的性质。掌握不定积分的基本 公式。掌握不定积分的换元积分法和分部积分法。会求有理函数、三角函数有理式和简单无 理函数的积分。 定积分:理解定积分的概念和几何意义。理解定积分的性质和定积分中值定理。理解积 分上限的函数性质及其求导。掌握牛顿(Newton)—莱布尼兹(Leibniz)公式。掌握定积分的 换元积分法和分部积分法。掌握建立定积分表达式的元素法(微元法),会用定积分表达和 计算一些几何量和物理量(平面图形的面积、平面曲线的弧长、旋转体的体积、平行截面面 积为已知的立体体积、变力作功、引力、压力和函数平均值)。了解广义积分及其收敛性的 概念。 2.重点、难点 重点:不定积分、定积分的换元积分法、分部积分法,积分上限的函数及其求导定理, 牛顿–莱布尼兹公式。 难点:换元积分法,微元法. 3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。 (四)常微分方程(10 学时) 内容:微分方程的基本概念,可分离变量的微分方程,齐次方程,一阶线性微分方程, 特殊类型的二阶微分方程,高阶线性微分方程,二阶常系数齐次线性微分方程,二阶常系数 非齐次线性微分方程. 1.基本要求 微分方程的基本概念:了解微分方程以及微分方程的解、通解、初始条件和特解的概念 一阶微分方程:掌握变量可分离的方程和一阶线性微分方程的解法。会解齐次方程、伯 努利方程。会用简单的变量代换求解某些微分方程。 二阶微分方程:会用降阶法求解三类方程 ( ) // // / ( ), ( , ), ( , ) n y f x y f x y y f y y = = = ,理解线性 微分方程解的性质和解的结构定理。掌握二阶常系数齐次线性微分方程的解法,了解高阶常 系数齐次线性微分方程的解法。会求自由项为 ( ) , x P x e n ( cos sin ) x e A x B x + 的二阶常系数 非齐次线性微分方程的特解,其中 ( ) P x n 为实系数 n 次多项式, , , , A B 为实数。 2.重点、难点
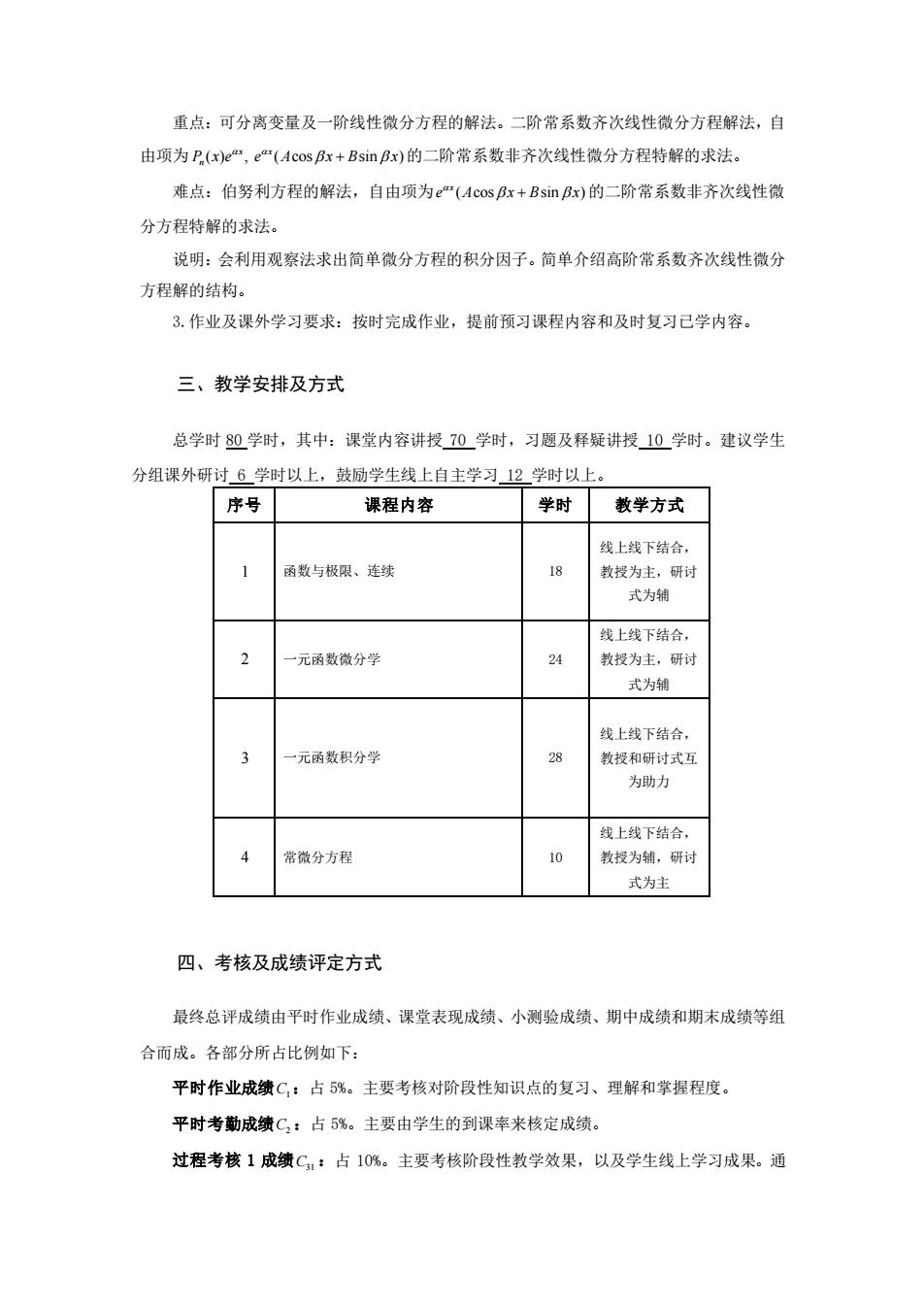
重点;可分离变量及一阶线性微分方程的解法。二阶常系数齐次线性微分方程解法,自由项为P,(x)e,e"(Acosβx+Bsinβx)的二阶常系数非齐次线性微分方程特解的求法。难点:伯努利方程的解法,自由项为e(Acosβx+Bsinβx)的二阶常系数非齐次线性微分方程特解的求法。说明:会利用观察法求出简单微分方程的积分因子。简单介绍高阶常系数齐次线性微分方程解的结构。3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。三、教学安排及方式总学时80学时,其中:课堂内容讲授70学时,习题及释疑讲授10学时。建议学生分组课外研讨6学时以上,鼓励学生线上自主学习12学时以上。序号课程内容学时教学方式线上线下结合,函数与极限、连续18教授为主,研讨式为辅线上线下结合,一元函数微分学教授为主,研讨224式为辅线上线下结合,一元函数积分学28教授和研讨式互为助力线上线下结合,常微分方程10教授为辅,研讨式为主四、考核及成绩评定方式最终总评成绩由平时作业成绩、课堂表现成绩、小测验成绩、期中成绩和期末成绩等组合而成。各部分所占比例如下:平时作业成绩C:占5%。主要考核对阶段性知识点的复习、理解和掌握程度。平时考勤成绩C:占 5%。主要由学生的到课率来核定成绩。过程考核1成绩Ci:占10%。主要考核阶段性教学效果,以及学生线上学习成果。通
重点:可分离变量及一阶线性微分方程的解法。二阶常系数齐次线性微分方程解法,自 由项为 ( ) , x P x e n ( cos sin ) x e A x B x + 的二阶常系数非齐次线性微分方程特解的求法。 难点:伯努利方程的解法,自由项为 ( cos sin ) x e A x B x + 的二阶常系数非齐次线性微 分方程特解的求法。 说明:会利用观察法求出简单微分方程的积分因子。简单介绍高阶常系数齐次线性微分 方程解的结构。 3.作业及课外学习要求:按时完成作业,提前预习课程内容和及时复习已学内容。 三、教学安排及方式 总学时 80 学时,其中:课堂内容讲授 70 学时,习题及释疑讲授 10 学时。建议学生 分组课外研讨 6 学时以上,鼓励学生线上自主学习 12 学时以上。 序号 课程内容 学时 教学方式 1 函数与极限、连续 18 线上线下结合, 教授为主,研讨 式为辅 2 一元函数微分学 24 线上线下结合, 教授为主,研讨 式为辅 3 一元函数积分学 28 线上线下结合, 教授和研讨式互 为助力 4 常微分方程 10 线上线下结合, 教授为辅,研讨 式为主 四、考核及成绩评定方式 最终总评成绩由平时作业成绩、课堂表现成绩、小测验成绩、期中成绩和期末成绩等组 合而成。各部分所占比例如下: 平时作业成绩 C1:占 5%。主要考核对阶段性知识点的复习、理解和掌握程度。 平时考勤成绩 C2 :占 5%。主要由学生的到课率来核定成绩。 过程考核 1 成绩 C31 :占 10%。主要考核阶段性教学效果,以及学生线上学习成果。通

过慕课学习及完成慕课测试来核定成绩。过程考核2成绩Cz:占10%。主要考核阶段性教学效果,及学生随堂听课效果。主要由教师的随堂测试来核定成绩。题型为:单选题,多选题,讨论题等期中考试成绩C:占30%。主要考核前半学期高等数学基础知识的系统掌握程度。书面考试形式。题型为:选择题、填空题、计算题、证明题等。期末考试成绩C:占40%。主要考核所在学期高等数学基础知识的系统掌握程度。书面考试形式。题型为:选择题、填空题、计算题、证明题等。过程成绩提交时间和总评成绩计算说明表成绩名称或说明成绩提交时间课程结束后,一周内提交成绩。平时作业成绩,采用5分制CC课程结束后,一周内提交成绩。到课率,采用5分制募课测试成绩,采用百分制,Ct慕课测试后。。一周内提交成绩系数 0.05≤x,≤0.1随堂测试,采用百分制课程结束后,一周内提交成绩Cn系数0.05≤x/≤0.1期中考试成绩,采用百分制,期中考试后,一周内提交成绩。C系数0.1≤x,≤0.3期末考试成绩,采用百分制,期末考试后,一周内提交成绩Cs系数0.2≤x,≤0.4总评成绩C=G+C+xC+xC.+xC注:上表用于说明授课过程中分项成绩提交时间,教师应在规定的时间内提交对应成绩,提前或逾期无法提交,一旦提交无法修改。大纲可以根据需要自行定义提交成绩的次数、时间和名称或说明,总评成绩计算必须与考核和成绩评定方式中描述的一致。五、教材及参考书目教材:同济大学编,《高等数学》(第七版),北京:高等教育出版社,2006.参考书目:[1]李忠、周建莹,高等数学(第2版),北京大学出版社,2009
过慕课学习及完成慕课测试来核定成绩。 过程考核 2 成绩 C32 :占 10%。主要考核阶段性教学效果,及学生随堂听课效果。主要 由教师的随堂测试来核定成绩。题型为:单选题,多选题,讨论题等 期中考试成绩 C4 :占 30%。主要考核前半学期高等数学基础知识的系统掌握程度。书面 考试形式。题型为:选择题、填空题、计算题、证明题等。 期末考试成绩 C5 :占 40%。主要考核所在学期高等数学基础知识的系统掌握程度。书面 考试形式。题型为:选择题、填空题、计算题、证明题等。 过程成绩提交时间和总评成绩计算说明表 成绩 成绩提交时间 名称或说明 C1 课程结束后,一周内提交成绩. 平时作业成绩,采用 5 分制 C2 课程结束后,一周内提交成绩. 到课率,采用 5 分制 C31 慕课测试后。一周内提交成绩 慕课测试成绩,采用百分制, 系数 31 0.05 0.1 x C32 课程结束后,一周内提交成绩 随堂测试,采用百分制 系数 31 0.05 0.1 x C4 期中考试后,一周内提交成绩. 期中考试成绩,采用百分制, 系数 4 0.1 0.3 x C5 期末考试后,一周内提交成绩. 期末考试成绩,采用百分制, 系数 5 0.2 0.4 x 总评成绩 C C C x C x C x C = + + + + 1 2 3 3 4 4 5 5 注:上表用于说明授课过程中分项成绩提交时间,教师应在规定的时间内提交对应成绩,提 前或逾期无法提交,一旦提交无法修改。大纲可以根据需要自行定义提交成绩的次数、时间 和名称或说明,总评成绩计算必须与考核和成绩评定方式中描述的一致。 五、教材及参考书目 教材:同济大学编,《高等数学》(第七版),北京:高等教育出版社,2006. 参考书目: [1]李忠、周建莹, 高等数学(第 2 版), 北京大学出版社, 2009

[2]清华大学编,《高等数学》,高等教育出版社,1985.[3]杨有龙等编,《高等数学同步辅导》,西安电子科技大学出版社,2016六、说明(一)与相关课程的分工衔接学习高等数学的目的,不仅仅在于学到一些数学的概念、公式和结论,更重要的是要了解数学的思想方法和精神实质,真正掌握数学这门学科的精髓。只有这样,所学的数学知识才不至沦为一堆僵死的教条。相反,若能做到触类旁通,则在现实世界中提出的种种问题面前数学会显示出无穷无尽的威力,终生受用不尽。高等数学,单靠教师把课讲好是远远不够的。只有调动学生学习的积极性和主动性,促使他们自觉地接受经常、充分而又严格的数学训练,才能使他们真正走近数学,获得切身的体会,从而加深对数学的理解。高等数学的任何章节,所有概念和定理无不是由严密的逻辑关系网编织连接在一起的。可以说,数学的逻辑结构乃是数学科学的本质与灵魂,是它的原理和精神所在。我们在教学过程中,一定要结合具体而生动的实例加以理解,还抽象数学以现实本性,使学生觉得数学是活的、生动的具体的,而且要体会到它为什么会是这样的,为什么必然是这样的,做到知其然,更要做到知其所以然。(二)其他说明为了提高学生的自主学习能力和增加学生的阅读量,既指定具体的教材[同济大学编,《高等数学》(第七版),北京:高等教育出版社,2006.],又鼓励教师、学生多参考、阅读自主学习其他教材和辅导材料。(执笔人:张丽审核人:杨有龙)2020年9月20日
[2]清华大学编,《高等数学》,高等教育出版社,1985. [3]杨有龙等编,《高等数学同步辅导》,西安电子科技大学出版社,2016. 六、说明 (一)与相关课程的分工衔接 学习高等数学的目的,不仅仅在于学到一些数学的概念、公式和结论,更重要的是要了 解数学的思想方法和精神实质,真正掌握数学这门学科的精髓。只有这样,所学的数学知识 才不至沦为一堆僵死的教条。相反,若能做到触类旁通,则在现实世界中提出的种种问题面 前数学会显示出无穷无尽的威力,终生受用不尽。高等数学,单靠教师把课讲好是远远不够 的。只有调动学生学习的积极性和主动性,促使他们自觉地接受经常、充分而又严格的数学 训练,才能使他们真正走近数学,获得切身的体会,从而加深对数学的理解。高等数学的任 何章节,所有概念和定理无不是由严密的逻辑关系网编织连接在一起的。可以说,数学的逻 辑结构乃是数学科学的本质与灵魂,是它的原理和精神所在。我们在教学过程中,一定要结 合具体而生动的实例加以理解,还抽象数学以现实本性,使学生觉得数学是活的、生动的、 具体的,而且要体会到它为什么会是这样的,为什么必然是这样的,做到知其然,更要做到 知其所以然。 (二)其他说明 为了提高学生的自主学习能力和增加学生的阅读量,既指定具体的教材[同济大学编, 《高等数学》(第七版),北京:高等教育出版社,2006.],又鼓励教师、学生多参考、阅读、 自主学习其他教材和辅导材料。 (执笔人:张丽 审核人:杨有龙) 2020 年 9 月 20 日