
西安毛子科技大学数学与统计学院XIDIAN UNIVERSITYSchool ofmathematies andstatistics西等数学第二节数列的极限西电高数团队ece68988e888ee86pee8
第二节 数列的极限

西安毛子科技大学数列的极限XIDIAN UNIVERSITY一、数列极限的描述性定义引例1 圆面积的计算圆内接正三角形的面积A圆内接正六边形的面积A圆内接正3×2n-1边形的面积A,n越大A,越接近于圆的面积
圆内接正三角形的面积 一、数列极限的描述性定义 引例1 圆面积的计算 A1 圆内接正六边形的面积 A2 圆内接正32 n-1边形的面积 A n n 越大 A n 越接近于圆的面积 数列的极限
西安毛子科技大学数列的极限XIDIAN UNIVERSITY刘“割圆术”徽1失与称少,厂制n无限增大吴至圆一于不了之称周一店割之可体细A,无限接近于圆的面积一又割司而割所关T无所则
刘 徽 “ 割 之 弥 细 , 所 失 弥 少 , 割 之 又 割 , 以 至 于 不 可 割 , 则 与 圆 周 合 体 而 无 所 失 矣 ” “割圆术” n 无限增大 A n 无限接近于圆的面积 数列的极限
西安毛子科技大学数列的极限XIDIAN UNIVERSITY定义1按照下标n从小到大排列得到的一列数x,X2,通项称为数列,简记为(x}。无穷数列数列中的每一个数称为数列的项,第n项x,叫做数列的一般项(通项)说明数列(x可看做数轴上的一个动点XixX0X3x4x
定义1 按照下标n 从小到大排列得到的一列数 1 2 n x x x , , , , 称为数列,简记为 { } xn . 数列中的每一个数称为数列的项,第 n 项 xn 叫做数列的 一般项(通项). 说明 数列 { } xn 可看做数轴上的一个动点. 通项 无穷数列 1 x 0 x4 x 2 x 3 x n x 数列的极限

西安毛子科技大学数列的极限XIDIANUNIVERSITY问题当n无限增大时,x,是否无限地接近于某个常数?定义2数列极限的定义(描述性)如果当n无限增大时,x无限接近于常数α,则称α为(xn)的极限,或称(x)收敛于α记为 limx,=α 或 x,→α(n→)
数列的极限 n 无限增大时, n 问题 当 x 是否无限地接近于某个常数? 数列极限的定义 如果当 n 无限增大时, { }n x 的极限,或称 { } xn 收敛于 a . xn 无限接近于常数 a , 记为 lim n n x a → = ( ) n 或 x a n → → 定义2 (描述性) 则称 a 为
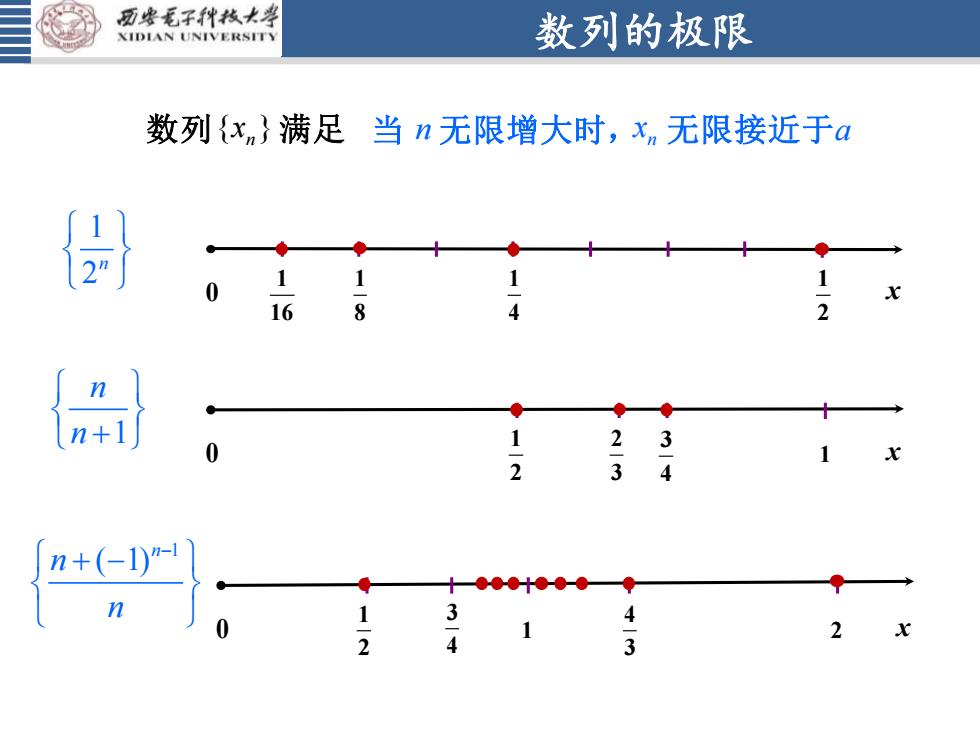
西安毛子科技大学数列的极限XIDIANUNIVERSITS数列(x)满足,当 n无限增大时,x,无限接近于a2n11110x814216 n+l21301x234n+(-1)"n3-41-24012t13
数列的极限 1 2 1 2 4 3 0 x 3 4 1 2 1 4 1 8 1 16 0 x 1 1 2 2 3 3 4 0 x 1 2 n 1 n n + 1 ( 1)n n n - + - 数列 { } xn 满足 当 n 无限增大时, xn 无限接近于 a
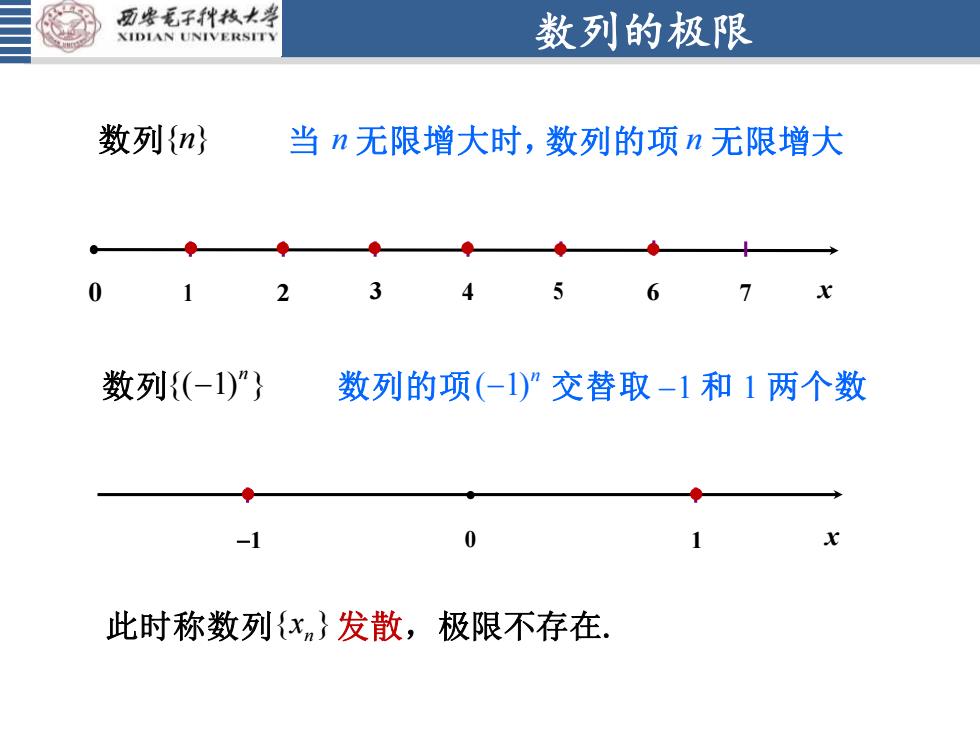
西安毛子科技大学数列的极限XIDIANUNIVERSITS数列(n)当n无限增大时,数列的项n无限增大30125x467数列(-1)")数列的项(-1)"交替取-1和 1两个数0-11x此时称数列x发散,极限不存在
数列的极限 0 1 2 3 4 5 6 7 x -1 0 1 x 数列 { }n 当 n 无限增大时,数列的项 n 无限增大 数列 {( 1) }n - 数列的项 ( 1) 交替取 -1 和 1 两个数 n - 此时称数列 { } xn 发散,极限不存在
西安毛子科技大学数列的极限XIDIAN UNIVERSITY二、数列极限的定义描述性定义的优点:直观、易懂、可以用来推测极限,缺点:定义中的“无限接近”只能靠直观感觉,没有给出定量的度量当n无限大时当n无限增大时[x-α|无限小x无限接近于a
数列的极限 二、数列极限的定义 缺点:定义中的“无限接近”只能靠直观感觉, 没有给出定量的度量. 描述性定义的优点:直观、易懂、可以用来推测极限. 当 n 无限增大时 xn 无限接近于 a 当 n 无限大时 - x a n 无限小

西要毛子科技大学数列的极限XIDIANUNIVERSIT问题当lx-aαl10即可!要使|x,-1|1000即可!对于任意正数ε,要使|x,-1二即可!8
数列的极限 问题 当 x a n - ? 时, xn 无限接近于a ? 例如 1 ( 1)n n n x n - + - = , 1 1 n x n - = , 1 0.1 n 要使 - x , 只要 n 10 即可! 要使 - xn 1 0.001, 只要 n 1000 即可! 1 n , 要使 - xn 1 , 只要 即可! 对于数列 对于任意正数
西安毛子科技大学数列的极限XIDIAN UNIVERSITS定义3若数列(x}与常数α 满足以下的关系:“3"2)ε-N定义对于任意给定的ε>0,总存在正整数N,limx,=a3n->a使当 n>N时,Ix,-α|0,E正整数N,则称常数α为数列(x)的极限,记作当n>N时,limx,=a 或 x,→a(n→0)n-+有x-a<.如果这样的α不存在,就称数列没有极限
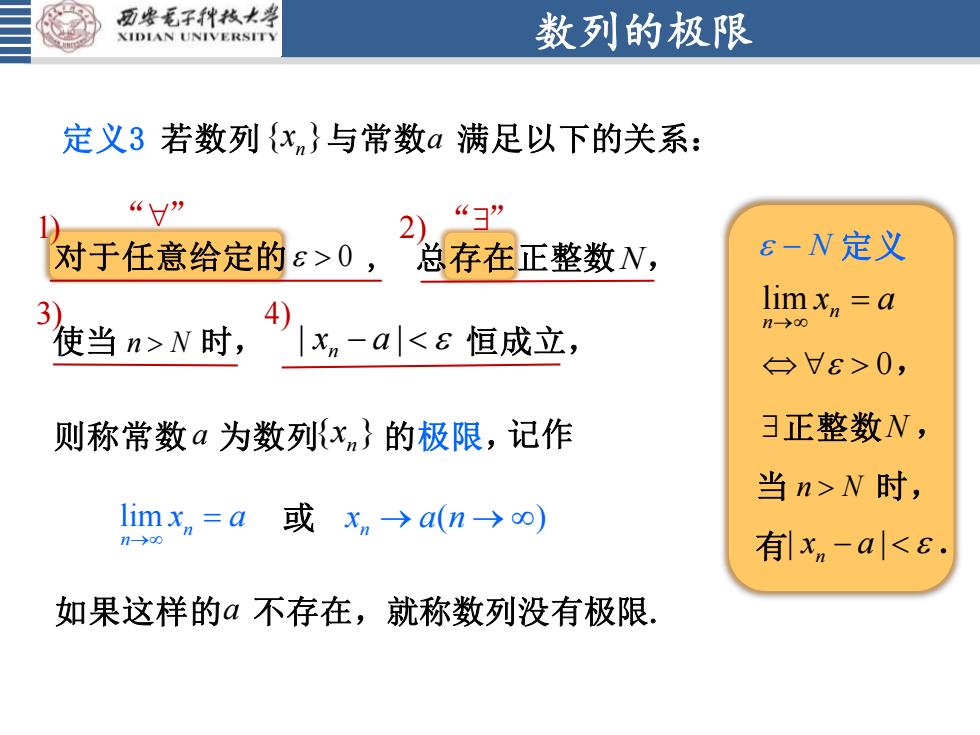
数列的极限 lim n n x a → = ( ) n x a n → → 1) 2) 3) 4) 定义3 若数列 { } xn 与常数 a 满足以下的关系: 对于任意给定的 0 , 总存在正整数 N , 使当 n N 时, - x a n 恒成立, 则称常数 a 为数列 { } xn 的极限,记作 或 如果这样的 a 不存在,就称数列没有极限. “” “” 0, lim n n x a → = n - x a . 正整数 N , 当 n N 时, 有 - N 定义