
第八章入一矩阵S1入一矩阵S4矩阵相似的条件S2入一矩阵的s5矩阵相似的条件标准形s6若当(Jordan)标准形S3不变因子的理论推导小结与习题
§2 λ-矩阵的 标准形 §3 不变因子 §1 λ-矩阵 §4 矩阵相似的条件 §6 若当(Jordan)标准形 的理论推导 §5 矩阵相似的条件 小结与习题 第八章 λ─矩阵

s 8.2 2一矩阵的标准形一、入一矩阵的初等变换二、入一矩阵的初等矩阵三、等价入一矩阵四、入一矩阵的对角化88.2入一矩阵的标准形A
§8.2 λ─矩阵的标准形 一、λ-矩阵的初等变换 二、λ-矩阵的初等矩阵 §8.2 λ─矩阵的标准形 三、等价λ-矩阵 四、λ-矩阵的对角化

一、入一矩阵的初等变换定义:入一矩阵的初等变换是指下面三种变换:①矩阵两行(列)互换位置;②矩阵的某一行(列)乘以非零常数c;③矩阵的某一行(列)加另一行(列)的(a)倍,p(a)是一个多项式.S8.2入一矩阵的标准形
§8.2 λ─矩阵的标准形 λ―矩阵的初等变换是指下面三种变换: ① 矩阵两行(列)互换位置; ② 矩阵的某一行(列)乘以非零常数c; ( ) 是一个多项式. ③ 矩阵的某一行(列)加另一行(列)的 ( ) 倍, 一、λ-矩阵的初等变换 定义:

注:为了书写的方便,我们采用以下记号[i,j代表ii两行(列)互换;[ic]代表第i行乘以非零数c;[i+@(l代表把第j行(列)的(a)倍加到第i行(列).S8.2入一矩阵的标准形A
§8.2 λ─矩阵的标准形 [ ( )] i c 代表第 i 行乘以非零数c ; [ ( ( ))] i j + 代表把第 j 行(列)的 ( ) 倍加到第 i 为了书写的方便,我们采用以下记号 [ , ] i j 代表 i j , 两行(列)互换; 注: 行(列)

二、入一矩阵的初等矩阵定义:将单位矩阵进行一次一矩阵的初等变换所得的矩阵称为一矩阵的初等矩阵注:①全部初等矩阵有三类:行0...1P(i,j) =行·..S8.2入一矩阵的标准形
§8.2 λ─矩阵的标准形 将单位矩阵进行一次 ―矩阵的初等变换所得的 矩阵称为 ―矩阵的初等矩阵. 二、λ-矩阵的初等矩阵 定义: 注: ① 全部初等矩阵有三类: i行 j行 1 1 0 1 1 0 1 1 P i j ( , ) =
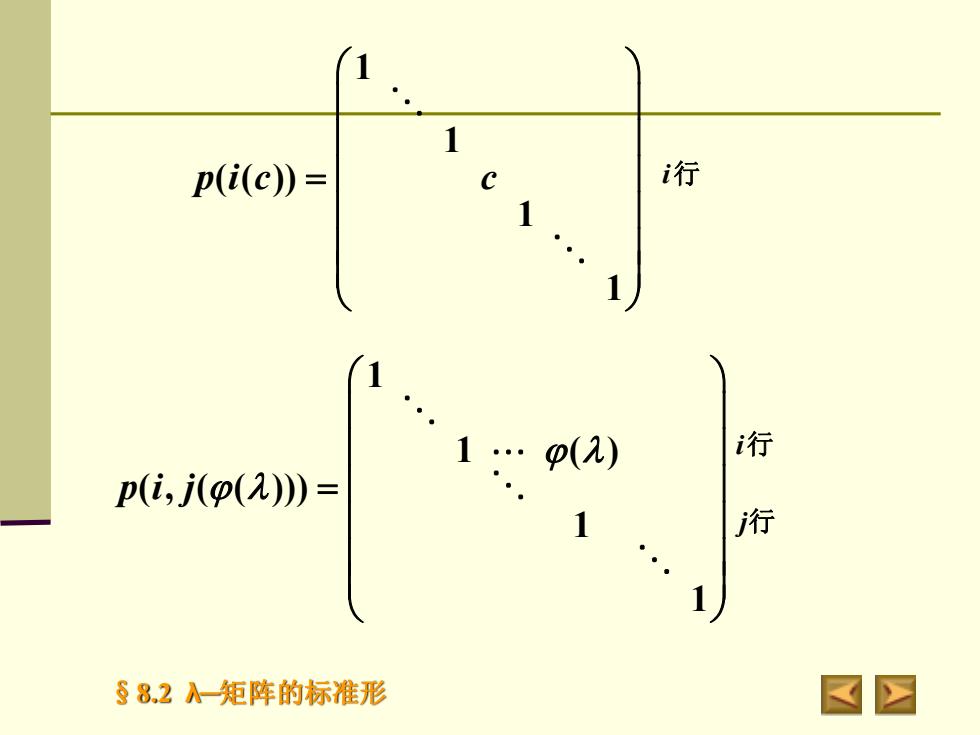
行p(i(c) =i行p(a)p(i, j(p(a) =j行1S8.2入一矩阵的标准形A
§8.2 λ─矩阵的标准形 1 1 ( ) ( , ( ( ))) 1 1 p i j = i行 j行 1 1 ( ( )) 1 1 p i c c = i行

②初等矩阵皆可逆p(i,j)-= p(i,ji)p(i(c)-1 = p(i())p(i, j(g(a)- = p(i, j(-p(a)))③对一个sxn的a一矩阵A(a)作一次初等行变换就相当于在A(a)在的左边乘上相应的s×s的初等矩阵;对A(a)作一次初等列变换就相当于在A(a)的右边乘上相应的nxn的初等矩阵S8.2入一矩阵的标准形V
§8.2 λ─矩阵的标准形 ② 初等矩阵皆可逆. 1 p i j p i j ( , ) ( , ) − = 1 1 ( ( )) ( ( )) c p i c p i − = 1 p i j p i j ( , ( ( ))) ( , ( ( ))) − = − ③ 对一个 s n 的 ―矩阵 A( ) 作一次初等行变换 就相当于在 A( ) 在的左边乘上相应的 s s 的初等矩 阵;对 A( ) 作一次初等列变换就相当于在 A( ) 的右 边乘上相应的 n n 的初等矩阵

三、等价入一矩阵定义:α一矩阵 A(a)若能经过一系列初等变换化为 一矩阵B(a),则称 A(a)与B(a)等价.性质:1)一矩阵的等价关系具有:反身性:A(2)与自身等价.对称性: A(a)与 B(a) 等价= B(a)与 A(a) 等价传递性: A(a)与 B(a)等价,B(a)与C(a)等价= A(a)与C(a)等价.S8.2入一矩阵的标准形区区
§8.2 λ─矩阵的标准形 为 -矩阵 B( ) ,则称 A( ) 与 B( ) 等价. ―矩阵 A( ) 若能经过一系列初等变换化 1) ―矩阵的等价关系具有: 反身性: A( ) 与自身等价. 对称性: A( ) 与 B( ) 等价 B( ) 与 A( ) 等价. 传递性: A( ) 与 B( ) 等价, B( ) 与 C( ) 等价 A( ) 与C( ) 等价. 三、等价λ-矩阵 定义: 性质:

2) A(a)与 B(a) 等价 存在一系列初等矩阵P....Ps.Q...Q, 使 A(a) = P.... P,B(a)Q....Q.四、入一矩阵的对角化设一矩阵A()的左上角元素au(a)0,1.(引理)且A(a)中至少有一个元素不能被它整除,那么一定可以找到一个与 A(a)等价的矩阵 B(),它的左上角元素b,(a)±0,且 a(b,()<a(au(a)) 88.2入一矩阵的标准形区区
§8.2 λ─矩阵的标准形 2) A( ) 与 B( ) 等价 存在一系列初等矩阵 1 1 , P P Q Q S t 使 1 1 ( ) ( ) . A P P B Q Q = S t 1.(引理)设 ―矩阵 A( ) 的左上角元素 11 a ( ) 0, 且 A( ) 中至少有一个元素不能被它整除,那么一定 可以找到一个与 A( ) 等价的矩阵 B( ) ,它的左上 角元素 b11( ) 0 ,且 ( ( )) ( ( )) b a 11 11 . 四、λ-矩阵的对角化

证:根据 A(a)中不能被an(a)除尽的元素所在的位置,分三种情形来讨论:i) 若在 A(a)的第一列中有一个元素 ai(a)不能被au(a) 除尽, 则有 ai()=a()g(a)+r(),其中余式 r(a)0,且 a(r(x))<a(au(a)对A()作下列初等行变换:an(a) .au(a)A(2) =[i-1(q]]r(a)ai(a)S8.2入一矩阵的标准形A
§8.2 λ─矩阵的标准形 证:根据 A( ) 中不能被 a11( ) 除尽的元素所在的 位置,分三种情形来讨论: i) 若在 A( ) 的第一列中有一个元素 ai1 ( ) 不能被 11 a ( ) 除尽, 其中余式 r( ) 0 ,且 (r x a ( ) ( ) ) ( 11 ) 对 A( ) 作下列初等行变换: 11 11 1 ( ) ( ) ( ) [ 1( )] ( ) ( ) i a a A i q a r = − 1 11 ( ) ( ) ( ) ( ), i 则有 a a q r = +