西安电子科技大学：《高等代数》课程PPT教学课件（讲稿）第八章 λ-矩阵 8.6 若当标准形的理论推导

第八章入一矩阵S1入一矩阵S4矩阵相似的条件S2入一矩阵的S5矩阵相似的条件标准形s6若当(Jordan）标准形S3不变因子的理论推导小结与习题

§2 λ－矩阵的 标准形 §3 不变因子 §1 λ－矩阵 §4 矩阵相似的条件 §6 若当(Jordan)标准形 的理论推导 §5 矩阵相似的条件 小结与习题 第八章 λ─矩阵

$ 8.6若当标准形的理论推导一、若当块的初等因子二、若当形矩阵的初等因子三、若当标准形存在定理88.6若当标准形的理论推导

§8.6 若当标准形的理论推导 一、若当块的初等因子 二、若当形矩阵的初等因子 §8.6 若当标准形的理论推导 三、若当标准形存在定理

一、若当块的初等因子2.若当块J。=1020nxn的初等因子是（-）"S8.6若当标准形的理论推导一1

§8.6 若当标准形的理论推导 若当块 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 n n J          =         的初等因子是 ( 0 ) . n   − 一、若当块的初等因子

证：000(2-2000-1.-2aE-J。三·0001-2..00-12-20IXI[aE- J]=(a-2.)"此即aE-J.的n级行列式因子。又aE-J。有一个n-1级子式是$8.6若当标准形的理论推导

§8.6 若当标准形的理论推导 证： 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 n n E J             −   − − − =     −   − −   0 0 ( ) . n    E J − = − 此即 的 级行列式因子. E J − 0 n 又 E J − 0 有一个 n − 1 级子式是

0-1 2- 200000-1=(-1)"..00-1 2-200-1所以aE-J.的n-1 级行列式因子为l.从而，aE-J。的n-2,,2,1级行列式因子皆为1.：J.的不变因子是：d,(a)=...= dn-i(a)=1, dn(a)=(a-2)".故J的初等因子是：（-）"S8.6若当标准形的理论推导A

§8.6 若当标准形的理论推导 ( ) 0 1 0 1 0 0 0 1 0 0 1 0 0 1 0 0 1 n     − − − − = − − − − 所以 的 级行列式因子为1. E J − 0 n − 1 从而， 的 级行列式因子皆为1. E J − 0 n − 2, ,2,1 0  J 的不变因子是: 1 1 0 ( ) ( ) 1, . ( ) ( ) n n n d d d      = = = = − − 故 的初等因子是: 0 J ( 0 ) . n   −

二、若当形矩阵的初等因子J若当形矩阵J=J.1012:其中J.=000...200.M;)k;xki则J的全部初等因子是：(a-z)hi, (a-2)h,.., (a-a)ks$8.6若当标准形的理论推导A

§8.6 若当标准形的理论推导 若当形矩阵 1 2 , s J J J J     =       其中 0 0 0 1 0 0 0 0 0 0 0 1 i i i i i i i k k J          =         则J的全部初等因子是： 1 2 1 2 ( ) , ( ) , , ( ) .s k k k       − − − s 二、若当形矩阵的初等因子

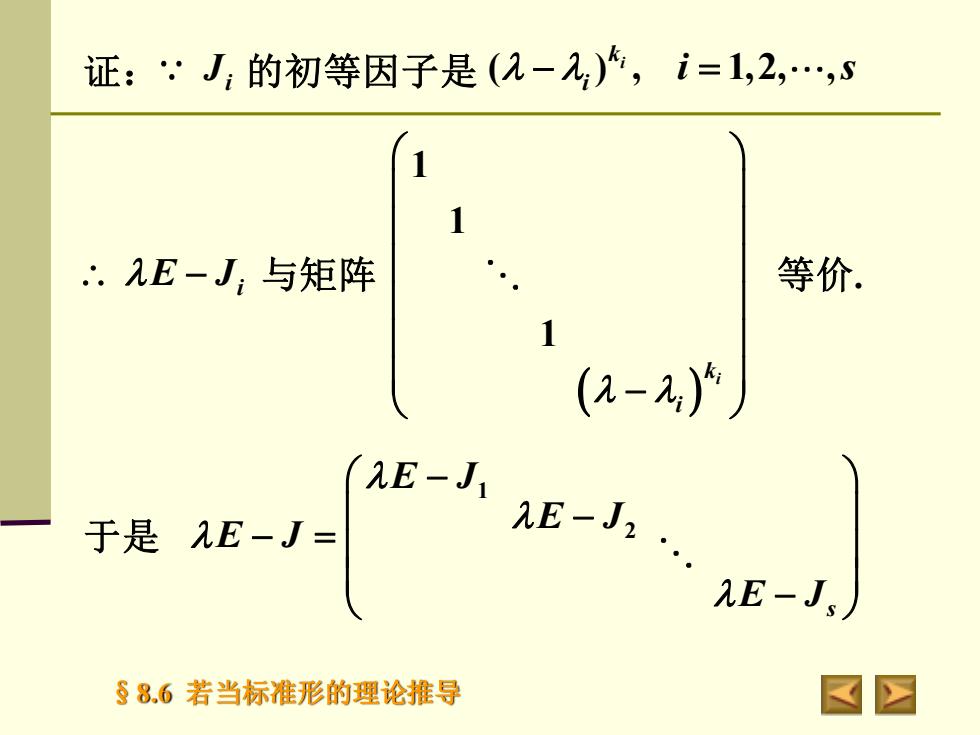
证：：J,的初等因子是(-a,)，i=1,2,,s等价：E-J与矩阵12(aE-JE-J,于是E-J=aE-JS8.6若当标准形的理论推导A

§8.6 若当标准形的理论推导 证： 的初等因子是 ( ) , 1,2, , i k i   − =i s i J  − E Ji 与矩阵 等价. ( ) 1 1 1 i k  i               −   于是 1 2 s E J E J E J E J       −   − − =     −  

与矩阵(a-D(a)=(a-2)(a-z,)"等价．由定理9，J的全部初等因子是：(a-a), (a-z)h, ..", (a-a,)h$8.6若当标准形的理论推导区区

§8.6 若当标准形的理论推导 与矩阵 D( ) = ( ) ( ) ( ) 1 2 1 2 1 1 1 1 1 1 s k k k s           − − −   等价. 由定理9， J 的全部初等因子是： 1 2 1 2 ( ) , ( ) , , ( ) .s k k k       − − − s

可见，每个若当形矩阵的全部初等因子就是它的全部若当块的初等因子构成的．由于每个若当块完全被它的级数与主对角线上的元素元.所刻划，而这两个数都反应在它的初等因子（α一因此，若当块被它的初等因子唯一决定从而，若当形矩阵除去其中若当块的排序外被它的初等因子唯一确定S8.6若当标准形的理论推导

§8.6 若当标准形的理论推导 初等因子唯一确定. 完全被它的级数与主对角线上的元素 0 所刻划， 而这两个数都反应在它的初等因子 上. 0 ( )n   − 可见，每个若当形矩阵的全部初等因子就是它 的全部若当块的初等因子构成的. 由于每个若当块 因此，若当块被它的初等因子唯一决定. 从而，若当形矩阵除去其中若当块的排序外被它的

三、若当标准形存在定理1.（定理10）每一个复矩阵A都与一个若当形矩阵相似，且这个若当形矩阵除去若当块的排序外是被矩阵A唯一决定的，它称为A的若当标准形$8.6若当标准形的理论推导

§8.6 若当标准形的理论推导 （定理10）每一个复矩阵A都与一个若当形矩阵 相似，且这个若当形矩阵除去若当块的排序外是 被矩阵A唯一决定的，它称为A的若当标准形. 三、若当标准形存在定理 1