西安电子科技大学：《高等代数》课程PPT教学课件（讲稿）第七章 线性变换 7.8 λ─矩阵介绍（若当标准形简介）

第七章线性变换S6线性变换的值域与核S1线性变换的定义S2线性变换的运算S7不变子空间s3线性变换的矩阵S8若当标准形简介S4特征值与特征向量89最小多项式85对角矩阵小结与习题

§2 线性变换的运算 §3 线性变换的矩阵 §4 特征值与特征向量 §1 线性变换的定义 §6线性变换的值域与核 §8 若当标准形简介 §9 最小多项式 §7不变子空间 小结与习题 第七章 线性变换 §5 对角矩阵

S 7.88入一矩阵介绍一、若当（Jordan）形矩阵二、若当（Jordan）标准形$7.8入一矩阵介绍

§7.8 λ─矩阵介绍 一、若当(Jordan)形矩阵 二、若当(Jordan)标准形 §7.8 λ─矩阵介绍

引入由87.5知，n维线性空间V的线性变换在某组基下的矩阵为对角形台有n个线性无关的特征向量，台α的所有不同特征子空间的维数之和等于n可见，并不是任一线性变换都有一组基，使它在这组基下的矩阵为对角形本节介绍，在适当选择基下，一般的线性变换的矩阵能化简成什么形状87.8入一矩阵介绍

§7.8 λ─矩阵介绍 由§7.5知，n维线性空间V的线性变换在某组基下 的矩阵为对角形   有n个线性无关的特征向量 .   的所有不同特征子空间的维数之和等于n . 可见，并不是任一线性变换都有一组基，使它在这 组基下的矩阵为对角形. 本节介绍，在适当选择基下，一般的线性变换的 矩阵能化简成什么形状. 引入

一、若当(Jordan)形矩阵定义：形式为元0.0001a...000J(a,t)=00..12000...012的矩阵称为若当（Jordan）块，其中a为复数：由若干个若当块组成的准对角矩阵称为若当形矩阵67.8入一矩阵介绍AV

§7.8 λ─矩阵介绍 0 0 0 0 1 0 0 0 ( , ) 0 0 1 0 0 0 0 1 t t J t           =         的矩阵称为若当(Jordan)块，其中  为复数； 一、若当(Jordan)形矩阵 定义：形式为 由若干个若当块组成的准对角矩阵称为若当形矩阵

200((i 0)(619)如：都是若当块；一，ii而下面的准对角形则是一个若当形矩阵。0(J(1,2)000000J(4,1)000R0J(-i,3)0100-1注：一级若当块就是一级矩阵，从而对角矩阵都是若当形矩阵。67.8入一矩阵介绍区区

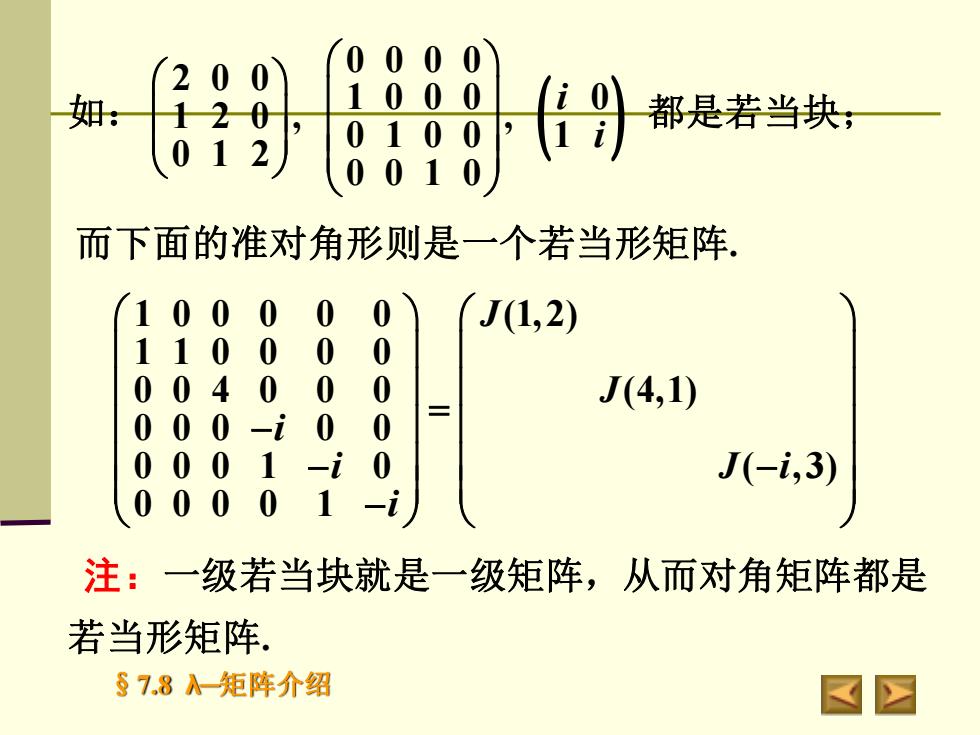
§7.8 λ─矩阵介绍 如： ( ) 0000 2 0 0 1 0 0 0 0 1 2 0 , , 0 1 0 0 1 0 1 2 0 0 1 0 i i                   都是若当块； 1 0 0 0 0 0 (1,2) 1 1 0 0 0 0 0 0 4 0 0 0 (4,1) 0 0 0 0 0 0 0 0 1 0 ( ,3) 0 0 0 0 1 J J i i J i i             =     −     − −     − 而下面的准对角形则是一个若当形矩阵. 注：一级若当块就是一级矩阵，从而对角矩阵都是 若当形矩阵

二、若当(Jordan)标准形1、设是复数域C上n维线性空间的一个线性变换，在V中必存在一组基，使在这组基下的矩阵是若当形矩阵，并是除若当块的排列次序外，该若当形由α唯一决定，称之为的若当标准形2、任一n级复矩阵A总与某一若当形矩阵相似，并且除若当块的排列次序外，该若当形矩阵由矩阵A唯一决定，称之为矩阵A的若当标准形67.8入一矩阵介绍区区

§7.8 λ─矩阵介绍 1、设  是复数域C上n维线性空间的一个线性变换， 在V中必存在一组基，使  在这组基下的矩阵是若当 形矩阵，并是除若当块的排列次序外，该若当形由  唯一决定，称之为  的若当标准形. 二、若当(Jordan)标准形 2、任一n级复矩阵A总与某一若当形矩阵相似， 并且除若当块的排列次序外，该若当形矩阵由矩阵 A唯一决定，称之为矩阵A的若当标准形

3、在一个线性变换α的若当标准形中，主对角线上的元素是的特征多项式的全部根（重根按多数计算）。（1、2、3的证明将在第八章给出）67.8入一矩阵介绍一

§7.8 λ─矩阵介绍 3、在一个线性变换  的若当标准形中，主对角线 上的元素是  的特征多项式的全部根（重根按多数 （1、2、3的证明将在第八章给出） 计算）

附：有时也规定形式为2.-0一2..J(a,t) =00-00..0的矩阵为若当（Jordan）块$7.8入一矩阵介绍

§7.8 λ─矩阵介绍 1 0 0 0 0 0 0 0 ( , ) 0 0 0 1 0 0 0 0 t t J t           =         的矩阵为若当(Jordan)块. 附：有时也规定形式为