
第五章二次型s5.1二次型的矩阵表示标准形$5.2S5.3唯一性S5.4正定二次型章小结与习题
第五章 二次型 §5.1 二次型的矩阵表示 §5.2 标准形 §5.3 唯一性 §5.4 正定二次型 章小结与习题

S5.2 标准形一、二次型的标准形二、合同的变换法三、小结$5.2标准形
§5.2 标准形 一、二次型的标准形 二、合同的变换法 三、小结 §5.2 标准形

二次型中非常简单的一种是只含平方项的二次型dx?+d,x,?+...+d,x.?它的矩阵是对角阵diag(d,,d,"".,dn)任意二次型能否经过适当非退化线性替换化成平方和的形式?若能,如何作非退化线性替换?85.2标准形人P
§5.2 标准形 二次型中非常简单的一种是只含平方项的二次型 它的矩阵是对角阵 平方和的形式?若能,如何作非退化线性替换? 任意二次型能否经过适当非退化线性替换化成 ? 2 2 2 1 1 2 2 n n d x d x d x + + + 1 2 1 2 0 0 0 0 ( , , , ) 0 0 0 n n d d diag d d d d =

一、二次型的标准形1、(定理1)数域P上任一二次型都可经过非退化线性替换化成平方和的形式证明:对二次型变量个数n作归纳法n=1时,f(x)=aux,结论成立.假定对n一1元二次型结论成立下面考虑n元二次型f(x,x2,.,x,)85.2标准形区区
§5.2 标准形 证明: 对二次型变量个数n作归纳法. 假定对n-1元二次型结论成立. 一、二次型的标准形 过非退化线性替换化成平方和的形式. 1、(定理1)数域P上任一二次型都可经 n=1时, 结论成立. 2 1 11 1 f x a x ( ) , = 下面考虑n元二次型 1 2 ( , , , ). n f x x x

f(xj,x2,.,xn)=ax +2a2xx2 +..+2ainxxn+ax, +...+ 2a2nX,xn+ax +.+2antgxn+...+a..x.?=dx*+2ax +2axx=dx*+2x2a*)+22ag*x-2?85.2标准形V
§5.2 标准形 2 1 2 11 1 12 1 2 1 1 ( , , , ) 2 2 n n n f x x x a x a x x a x x = + + + 2 22 2 2 2 2 n n + + + a x a x x 2 33 3 3 3 2 n n + + + a x a x x2 nn n + + a x 2 11 1 1 1 2 2 2 2 n n n j j ij i j j i j a x a x x a x x = = = = + + 2 11 1 1 1 2 2 2 2 n n n j j ij i j j i j a x x a x a x x = = = = + +

配方=arlx*+2x,Za'aym +(2aan-ar,x,)"l法0-a(ala,)+Zaxx,=228=an[x+(2a'ayx,)P-a(2a,)+2axx,j=2-=anlx +(Za'y)P+≥22bx;j=2i=2 j=22b*,=-a(24,)~+22agx,x这里,i=2 j=2i=2i-2 j-2是一个X2,X3,,x的n一1元二次型85.2标准形
§5.2 标准形 这里, 2 1 11 1 1 11 1 2 11 2 1 1 2 [ 2 ( ] ) n j j j n j j j a x x a a x a a x − = − = = + + 1 2 1 2 11 1 11 1 11 1 2 2 2 2 [ ( )] ( ) n n n n j j j j ij i j j j i j a x a a x a a x a x x − − = = = = = + − + 1 2 11 1 2 1 1 2 2 ( ) n n n ij i j i j j j j a x a a a x x − = = = − + 1 2 11 1 11 1 2 2 2 [ ( )] n n n j j ij i j j i j a x a a x b x x − = = = = + + 1 2 11 1 2 2 2 2 2 ( ) n n n n n ij i j j j ij i j i j j i j b x x a a x a x x − = = = = = = − + 是一个. 2 3 的n-1元二次型. , , , n x x x 配方 法
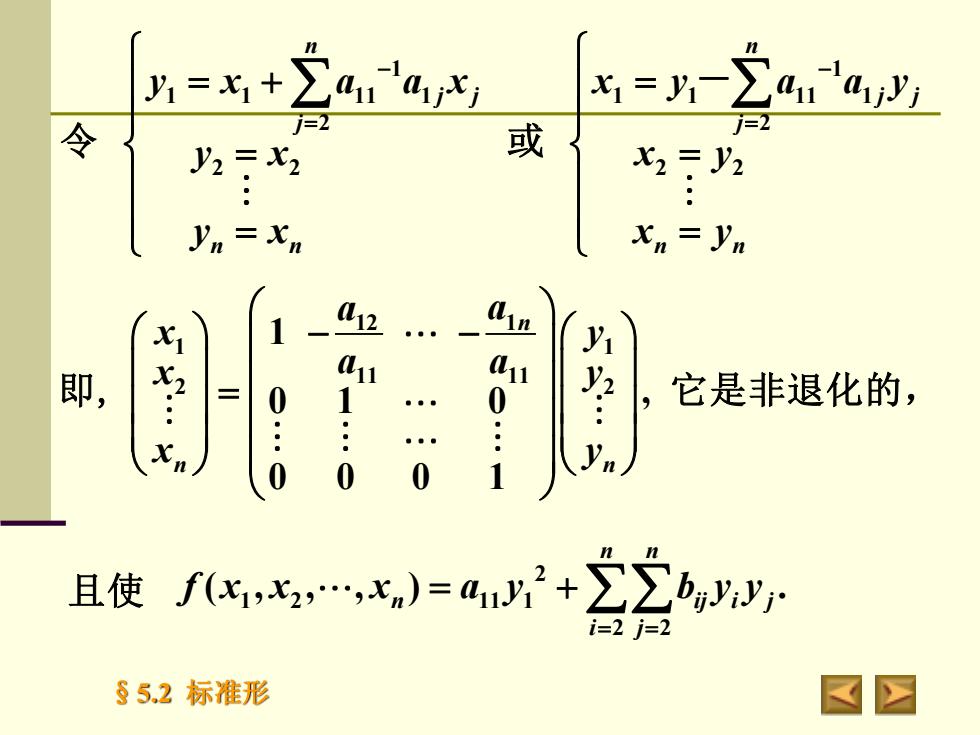
i =x +Ean-ajxa'ajy;X =yiJj=21=2或令X2 = y2y2 = X2...yn=xnXn=yn1ana12Xiy1auaii..y?即,,它是非退化的,100:......xn)yn0010ZZb且使 f(xi,X2,,xn)=auy+b,yiyji=2 j=285.2标准形区
§5.2 标准形 它是非退化的, 1 1 1 11 1 2 2 2 n j j j n n y x a a x y x y x − = = + = = 令 1 1 1 11 1 2 2 2 n j j j n n x y a a y x y x y − = = = = - 或 12 1 1 1 11 11 2 2 1 0 1 0 , 0 0 0 1 n n n a a x y a a x y x y − − = 即, 2 1 2 11 1 2 2 ( , , , ) . n n n ij i j i j f x x x a y b y y = = 且使 = +

Zbi,y,y有非退化线性替换由归纳假设,对i2i=2Z2 =C22J2+C23J3+..C2nJ'nZ3 =C32J2+C33J3 +...C3nynZn=Cn2J2+Cn3J'3+...CnnJ'n使它变成平方和dz+d,z+…+d,zn于是,非退化线性替换Z1 = y1Z2=C22J2+C23J'3 +..C2ny'n[zn =Cn2J2 +Cn3J' +..CnnJ'n85.2标准形
§5.2 标准形 使它变成平方和 于是,非退化线性替换 2 22 2 23 3 2 3 32 2 33 3 3 2 2 3 3 n n n n n n n nn n z c y c y c y z c y c y c y z c y c y c y = + + = + + = + + 1 1 2 22 2 23 3 2 2 2 3 3 n n n n n nn n z y z c y c y c y z c y c y c y = = + + = + + 2 2 2 2 2 3 3 n n d z d z d z + + + 由归纳假设,对 有非退化线性替换 2 2 n n ij i j i j b y y = =

就使f(x,x,,x)变成f(x,x2xn)=a1z? +d,z? +..+d,z.?Zn2)a=0,(i=1,2,…,n),但至少有一个 au,±0(j>1)不妨设a≠0,作非退化线性替换:X, = Ji+ y2X2 = Ji - 2X3=y3(Xn=yn85.2标准形A
§5.2 标准形 1 1 2 2 1 2 3 3 n n x y y x y y x y x y = + = − = = 2 2 2 1 2 11 1 2 2 ( , , , ) n n n f x x x a z d z d z = + + + 就使 f x x x ( , , , ) 1 2 n 变成 2) a i n ii = = 0,( 1,2, , ), 但至少有一个 1 0( 1) j a j 不妨设 a12 0, 作非退化线性替换:

则 f(x,x2,",xn)=2 E agxx,I<i<j≤n= 2a2Xx, +.= 2ai2(y1 + y2)(y1 - y2)+..= 2ai2J - 2ai2y? +这是一个Ji,J2,………,Jn的二次型,且J2的系数不为零.由情形1)知,结论成立。85.2标准形
§5.2 标准形 不为零. 由情形1)知,结论成立. 2 2 12 1 12 2 = − + 2 2 a y a y 12 1 2 1 2 = + − + 2 ( )( ) a y y y y 12 1 2 = + 2a x x 则 1 2 1 ( , , , ) 2 n ij i j i j n f x x x a x x = 这是一个 y y y 1 2 , , , n 的二次型,且 的系数 2 1 y