
§4.1矩阵的概念 一、矩阵的概念 二、矩阵的相等 三、一些特殊矩阵
一、矩阵的概念 二、矩阵的相等 三、一些特殊矩阵

一矩阵的定义1. 定义aia12.aina21a22.a2n数表称为一个s×n矩阵as1asnas2记作:(a;)sxn或Asxn84.1矩阵的概念
§4.1 矩阵的概念 ( ) . ij s n s n 记作: a A 或 一、矩阵的定义 1.定义 11 12 1 21 22 2 1 2 n n s s sn a a a a a a a a a 数表 称为一个 s n 矩阵.

二、矩阵的相等定义设矩阵A=(a;)sn,B=(bi;)kxI,若s=k, n=l, a, =bj, i=l,.",s,j=l,.",n则称矩阵A与B相等,记作A=B.84.1矩阵的概念
§4.1 矩阵的概念 , , , 1, , , 1, , ij ij s k n l a b i s j n = = = = = 二、矩阵的相等 ( ) , ( ) , 设矩阵 A a B b = = ij s n ij k l 若 则称矩阵A与B相等,记作 A=B. 定义
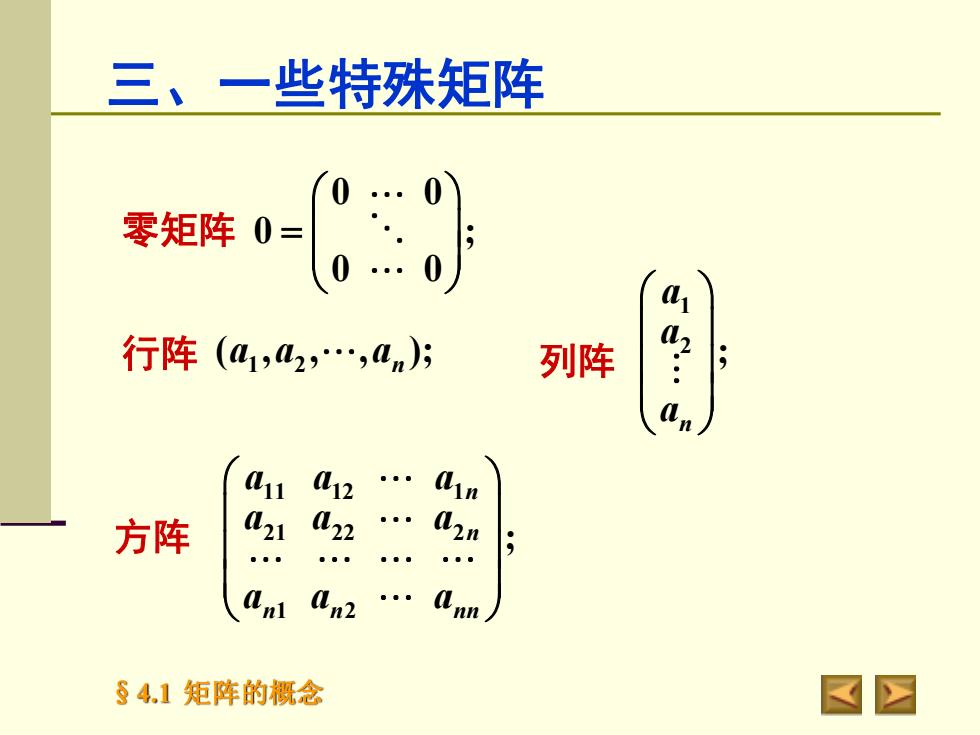
三、一些特殊矩阵零矩阵0=a..行阵(ai,a2,,an);列阵aua12aina21a22a2n方阵anlan2...ann84.1矩阵的概念
§4.1 矩阵的概念 三、一些特殊矩阵 零矩阵 0 0 0 ; 0 0 = 行阵 1 2 ( , , , ); n a a a 列阵 1 2 ; n a a a 方阵 11 12 1 21 22 2 1 2 ; n n n n nn a a a a a a a a a

对角矩阵diag(ar,.,an)=单位矩阵E-数量矩阵kE=S4.1矩阵的概念
§4.1 矩阵的概念 对角矩阵 1 1 0 ( , , ) ; 0 n n diag = 单位矩阵 1 0 ; 0 1 E = 数量矩阵 0 ; 0 k kE k =

负矩阵设 A=(a;)xn,矩阵-a -ai2 ...-ain-a21 -a22 ....-a2n-aml-as1...-asn称为A的负矩阵,记作一A即 -A=(-aj)sxn84.1矩阵的概念
§4.1 矩阵的概念 11 12 1 21 22 2 1 1 n n m s sn a a a a a a a a a − − − − − − − − − 负矩阵 设 A a = ( ) , ij s n 矩阵 称为A的负矩阵,记作-A . ( ) . 即 − = − A aij s n