
第二章行列式85行列式的计算S1引言s6行列式按行(列)展开82排列s3n级行列式7Cramer法则s8Laplace定理s4n级行列式的性质行列式乘法法则
§4 n 级行列式的性质 §8 Laplace定理 行列式乘法法则 §3 n 级行列式 §2 排列 §1 引言 §5 行列式的计算 §7 Cramer法则 §6 行列式按行(列)展开 第二章 行列式

$2.4行列式的性质一、行列式的性质二、 应用举例
一、行列式的性质 二、应用举例

转置行列式auia2aina22a2na21设 D=anannan2...ailanla21a22a12an2..行列式称为D的转置行列式,ainannazn...记作D'或DT.82.4行列式的性质人V下
§2.4 行列式的性质 转置行列式 11 21 1 12 22 2 1 2 n n n n nn a a a a a a a a a 行列式 11 12 1 21 22 2 1 2 , n n n n nn a a a a a a D a a a 设 = 称为D的转置行列式, 记作 或 . T D D

一、行列式的性质性质1行列互换,行列式不变,即D'=D,au0d212012n11a21an2a.aa2nann2a1nrR区下82.4行列式的性质
§2.4 行列式的性质 行列互换,行列式不变,即 11 12 1 11 21 1 21 22 2 12 22 2 1 2 1 2 n n n n n n nn n n nn a a a a a a a a a a a a a a a a a a = 一、行列式的性质 性质1 D D =

证: 记 D'=det(b,),其中 b,=aj,i,j-1,2,...,n按行列式的定义D'- E (-1)(i) ,bi, .bmi.ii...in- E (-1)(i aa2inii..in另一方面,按行列式的等价定义D可表成D= E(-1)(4) ,nji...in.. D'=D.82.4行列式的性质R下
§2.4 行列式的性质 记 det( ), D bij = 1 2 1 2 1 2 ( ) 1 2 ( 1) n n n i i i i i ni i i i D b b b = − 另一方面,按行列式的等价定义D可表成 证: , , 1,2, , ij ji 其中 b a i j n = = 按行列式的定义 1 2 1 2 1 2 ( ) 1 2 ( 1) n n n i i i i i i n i i i a a a = − 1 2 1 2 1 2 ( ) 1 2 ( 1) n n n i i i i i i n i i i D a a a = − = D D

性质2行列式某行(列)元素的公因子可提到行列式符号之外:即ayaylay2anap2n....··::.::...AairMa2..Aain=元aiai?Win..::.!.:anianannan2annan2.或者说,以一数乘行列式的一行(列)就相当于用这个数乘此行列式kr,kc;推论行列式中某一行(列)为零,则行列式为零R区F32.4行列式的性质
§2.4 行列式的性质 行列式某行(列)元素的公因子可提到 行列式符号之外.即 11 12 11 12 1 1 1 2 1 2 1 2 1 2 n n i i in i i in n n nn n n nn a a a a a a a a a a a a a a a a a a = 推论 行列式中某一行(列)为零,则行列式为零. 性质2 或者说,以一数乘行列式的一行(列)就相当于 用这个数乘此行列式. i kr i kc
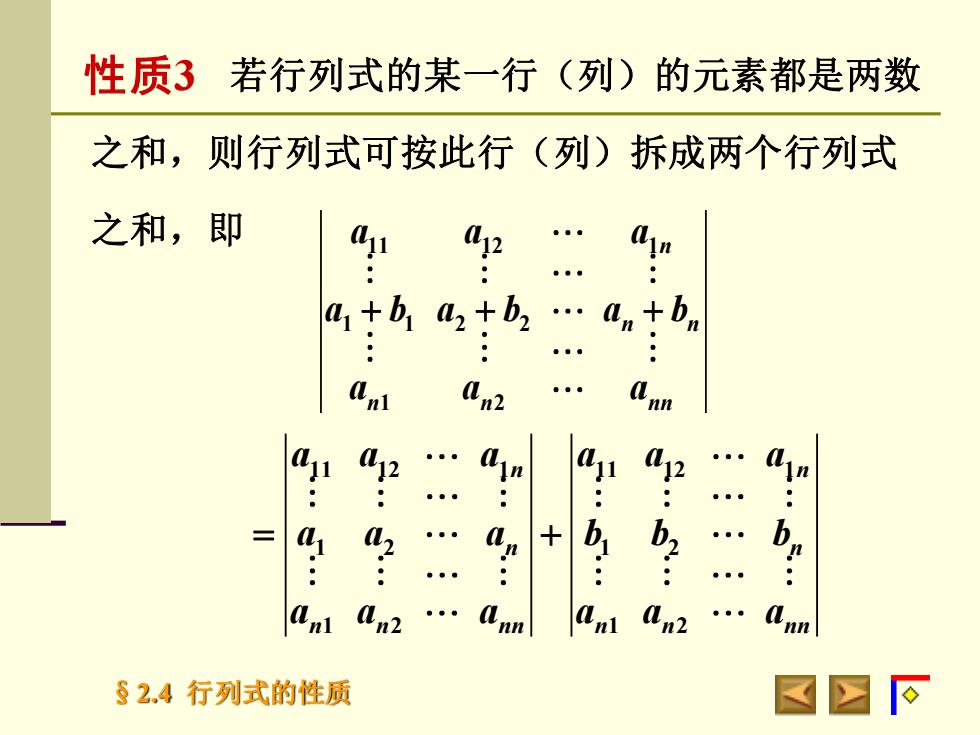
性质3若行列式的某一行(列)的元素都是两数之和,则行列式可按此行(列)拆成两个行列式之和,即ayiap2ayn.....+b,ai+b,a, +b,...a.-...anan2anna2aynay2::......"...b...十ananlannannan2an2下82.4行列式的性质
§2.4 行列式的性质 若行列式的某一行(列)的元素都是两数 11 12 1 11 12 1 1 2 1 2 1 2 1 2 n n n n n n nn n n nn a a a a a a a a a b b b a a a a a a = + 之和,则行列式可按此行(列)拆成两个行列式 之和,即 性质3 11 12 1 1 1 2 2 1 2 n n n n n nn a a a a b a b a b a a a + + +

性质4如果行列式中有两行(列)相同,那么行列式为0.(所谓两行相同指的是两行元素对应都相等)ay2ayn··.ai1ainai2证:设行列式 D=aaknak2.anlan2ann中第i行与第k行相同,冈区82.4行列式的性质
§2.4 行列式的性质 如果行列式中有两行(列)相同,那么 行列式为0. (所谓两行相同指的是两行元素对应都相等). 性质4 设行列式 11 12 1 1 2 1 2 1 2 n i i in k k kn n n nn a a a a a a D a a a a a a 证: = 中第 i 行与第 k 行相同

即,a, =au,j=1,2,,n,于是,D- Z (-1)auy-.m.ji..jn- E (-..ji..jn= E --1)ax.m.ji...jn- E (-am.jii...jn=-D:. D=0.区区下S2.4行列式的性质
§2.4 行列式的性质, 1,2, , , ij kj a a j n = = 1 1 2 1 2 ( ) 1 2 ( 1) i k n i k n n j j j j j j ij kj nj j j j D a a a a a = − 即, 1 1 2 1 2 ( ) 1 2 ( 1) i k n i k n n j j j j j j kj ij nj j j j a a a a a = − 1 1 2 1 2 ( ) 1 2 ( 1) k i n k i n n j j j j j j ij kj nj j j j a a a a a = − − 1 1 2 1 2 ( ) 1 2 ( 1) k i n k i n n j j j j j j ij kj nj j j j a a a a a = − − = −D = D 0. 于是

性质5行行列式中两行(列)成比例,则行列式为0.证:由性质2、性质4即得。性质6把行列式的某一行(列)的倍数加到另一r,+kr,c,+kc,行(列),行列式不变证:由性质3、性质5即得,性质7对换行列式中两行(列)位置,行列式反号。rαrjC,>C;RF82.4行列式的性质
§2.4 行列式的性质 行列式中两行(列)成比例,则行列式为0. 证:由性质2、性质4即得. 把行列式的某一行(列)的倍数加到另一 行(列),行列式不变. 证:由性质3、性质5即得. 性质5 性质6 性质7 对换行列式中两行(列)位置,行列式反号. i j r kr + i j c kc + i j r r i j c c