
*第八节 酉空间介绍 主要内容 定义 酉空间中的重要结论
第八节 菌空间介绍 主要内容 定义 国空间中的重要结论

一、定义欧氏空间是专对实数域上线性空间而讨论的酉空间实际就是复数域上的欧氏空间定义15设V是复数域上的线性空间,在V上定义了一个二元复函数,称为内积,记作(α,B)它具有以下性质:1)(α,β)=(β,α),这里(β,α)是(β,α)的共轭复数;
一、定义 欧氏空间是专对实数域上线性空间而讨论的- 空间实际就是复数域上的欧氏空间. 定义 15 是复数域上的线性空间,在 上定义了一个二元复函数,称为内积,记作仰,舟, 它具有以下性质: 仰,舟=( ),这里( )是( )的 共辄复数;

2)(kα,β)=k(α,β)3)(α+β,)=(α,)+(β,);4)(α,α)是非负实数,且(α,α)=0当且仅当α=0.这里α,β,是V中任意的向量,k为任意复数,这样的线性空间称为酉空间
2) (k ,舟 仰,舟; 3) r) = r) + r); 仰, )是非负实数,且仰, )=。当且仅当 O. 这里 中任意的向量, 为任意复数, 这样的线性空间称为西空间

例在线性空间Cn中,对向量α =(αi, α2,..., αv), β=(Bi,β2, ...,β),定义内积为(1)(α, β)= αiβ +αβ +... + αvβy.显然,内积(1)满足定义15中的条件.这样Cn就成为一个酉空间
在线性空间。中,对向量 =(α1 ,的,..., αJ =(β1 ,践,..., v) ' 定义内积为 ,舟= α1β1 α2β2 + ... αvβv· (1) 显然,内积( )满足定义 15 中的条件.这样。就 成为一个 空间.

二、酉空间中的重要结论由于酉空间的讨论与欧氏空间的讨论很相似有一套平行的理论,因此这儿只简单地列出重要的结论,而不详细论证。首先由内积的定义可得到1) (α, kβ)= k(α,β) .2) (α,β+)=(α,β)+(α,).和欧氏空间一样,因为(α,α)≥0,故可定义向量的长度
二、菌空间中的重要结论 由于国空间的讨论与欧氏空间的讨论很相似, 有一套平行的理论,因此这儿只简单地列出重要的 结论,而不详细论证. 首先由内积的定义可得到 仰, kt = k 衍,舟. 2) + r) = )+( y). 和欧氏空间一样,因为仰, )三 ,故可定义 向量的长度.

3)/(α,α)叫做向量α的长度,记为「αl4)柯西-布涅柯夫斯基不等式仍然成立,即对任意的向量α,β有I(α,β)/≤αliβl,当且仅当α,β线性相关时,等号成立注意:酉空间中的内积(α,β)一般是复数,故向量之间不易定义夹角,但我们仍引入5)向量α,β,当(α,β=0时称为正交或互相垂直
3) ~( )叫做向量 的长度,记为| |· 柯西-布涅柯夫斯基不等式仍然成立,即对 任意的向量 |( ,均/刮 || |, 当且仅当 线性相关时,等号成立. 注意: 西空间中的内积仰,舟一般是复数, 故向量之间不易定义夹角,但我们仍引入 向量 ,当仰,舟= 时称为正交或互 相垂直.

在n维酉空间中,同样可以定义正交基和标准正交基,并且关于标准正交基也有下述一些重要性质:6)任意一组线性无关的向量可以用施密特过程正交化,并扩充成为一组标准正交基7)对n级复数矩阵A,用A表示以A的元素的共轭复数作元素的矩阵.如A满足ATA = AAT= E,则称之为酉矩阵.它的行列式的绝对值等于1
维国空间中,同样可以定义正交基和标准 正交基,并且关于标准正交基也有下述一些重要性 质: 任意一组线性无关的向量可以用施密特过 程正交化,并扩充成为一组标准正交基. 级复数矩阵 ,用互表示以 的元素 的共辄复数作元素的矩阵.如 满足 ATA=AAT=E, 则称之为茵矩阵.它的行列式的绝对值等于

两组标准正交基的过渡矩阵是酉矩阵,类似于欧氏空间的正交变换和对称矩阵,可以引进酉空间的酉变换和埃尔米特矩阵它们也分别具有正交变换和对称矩阵的一些重要性质,我们把它列举在下面:8)酉空间V的线性变换A,如果满足(Aα,Aβ)=(α, β)就称为V的一个酉变换。。酉变换在标准正交基下的矩阵是酉矩阵
两组标准正交基的过渡矩阵是国矩阵. 类似于欧氏空间的正交变换和对称矩阵,可以 引进固空间的西变换和埃尔米特矩阵.它们也分别 具有正交变换和对称矩阵的一些重要性质,我们把 它列举在下面: 菌空间 的线性变换 ,如果满足 (Aα Aβ)=( ), 就称为 的一个西变换.国变换在标准正交基下 的矩阵是国矩阵.
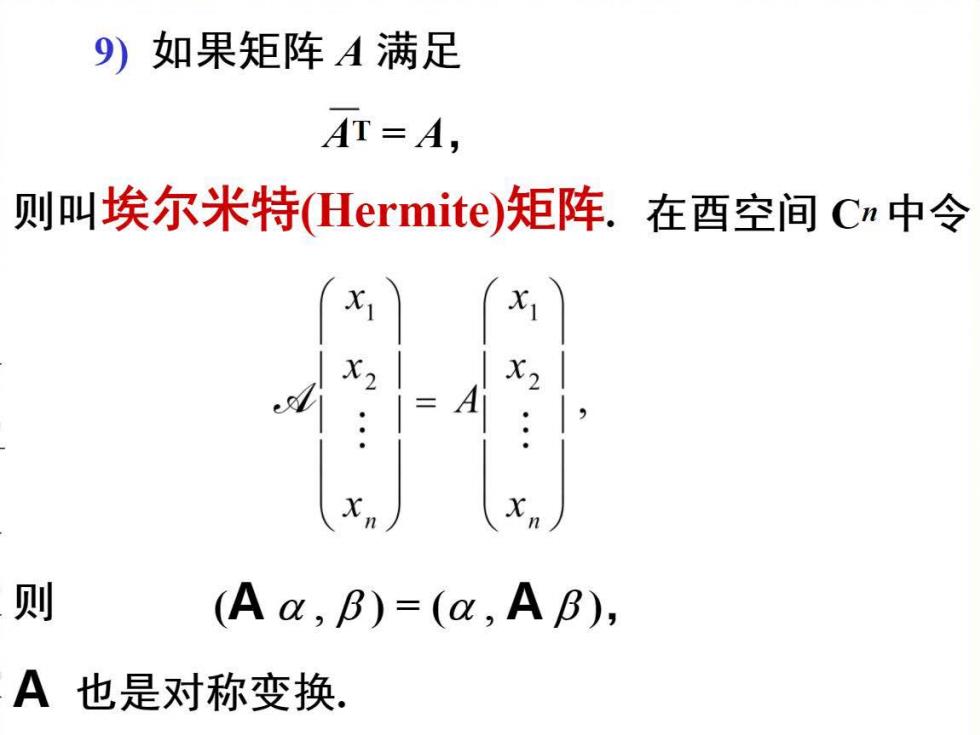
9)如果矩阵A满足AT= A,则叫埃尔米特(Hermite)矩阵.在酉空间Cn中令(x)x)X2X2...xn)Xn则(Aα,β)=(α,Aβ)A 也是对称变换
如果矩阵 满足 AT=A 则叫 埃尔米特(Hermite)矩阵.在国空间。中令 \ x 1llll / fill - \ x 1llll / Il --- X A x d • I I • • I I • χn ) n 则(Aα )=( Aβ), 也是对称变换.

10)V是酉空间,Vi是子空间,VI是Si的正交补,则V= Vi@ Vil.又设V是对称变换的不变子空间,则VI也是不变子空间。11)埃尔米特矩阵的特征值为实数.它的属于不同特征值的特征向量必正交12)若A是埃尔米特矩阵,则有酉矩阵C,使C-1AC = CTAC是对角形矩阵
10) 是固空间,只是子空间, V1..1_ 是白的 正交补,则 V = V1 EB V1 ..1_ • 又设只是对称变换的不变子空间,则只 是不变子空间. 11 埃尔米特矩阵的特征值为实数.它的属于 不同特征值的特征向量必正交. 12 是埃尔米特矩阵,则有菌矩阵 ,使 C-1AC= CTAC 是对角形矩阵.