
第二章行列式85行列式的计算S1引言s6行列式按行(列)展开82排列s3n级行列式7Cramer法则s8Laplace定理s4n级行列式的性质行列式乘法法则
§4 n 级行列式的性质 §8 Laplace定理 行列式乘法法则 §3 n 级行列式 §2 排列 §1 引言 §5 行列式的计算 §7 Cramer法则 §6 行列式按行(列)展开 第二章 行列式

s2.3n级行列式一、行列式定义二、n级行列式的等价定义
一、 行列式定义 二、n 级行列式的等价定义

一、行列式的定义1. 二级行列式air.ai2= A1422 - A1221azia222.三级行列式a11 a12 413a21 A22 A23= a1a22a33 +a12a23a31 +a13a21a32[a31 a32 a33]-a132231-1221a33-a112332s2.3n阶行列式R
§2.3 n阶行列式 一、行列式的定义 1. 二级行列式 11 12 21 22 a a a a 2. 三级行列式 11 22 12 21 = a a − a a 11 12 13 21 22 23 11 22 33 12 23 31 13 21 32 31 32 33 a a a a a a a a a a a a a a a a a a = + + 13 22 31 12 21 33 11 23 32 − − − a a a a a a a a a
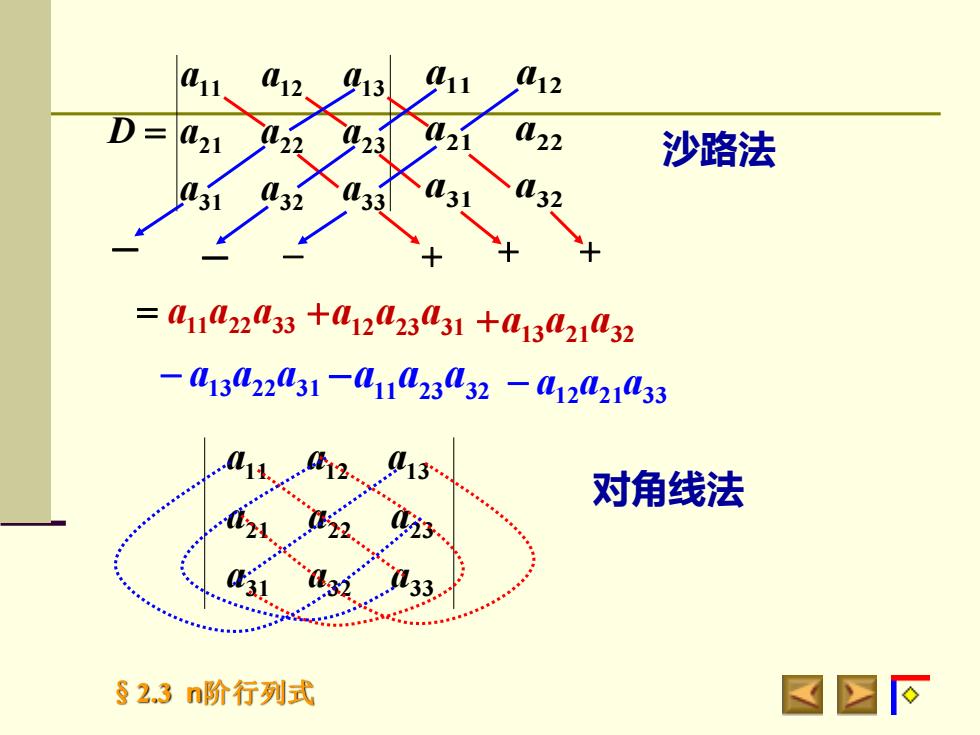
aa2913J11a12D=a21a22a22923a21沙路法a3!a32a31a32133++=a11a22a33 +a12a2331 +a13a21a32—a13a22a31—aii2332 -a12a21a331a13对角线法区s2.3n阶行列式
§2.3 n阶行列式 31 32 21 22 11 12 a a a a a a 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = − − − + + + 11 23 32 − a13a22a31 −a a a − a12a21a33 13 21 32 = a a a 11 22 33 +a a a 12 23 31 +a a a 沙路法 31 32 33 21 22 23 11 12 13 a a a a a a a a a 对角线法

3.n级行列式a aiz-- alina21 a22*.. a2nn 级行列式an an2".. ann等于所有取自不同行不同列的n个元素的乘积(1)aliazi".anin的代数和,这里jij,…jn为1,2,.…,n的排列.每一项(1)都按下列规则带有符号:当jijzjn为奇排列时(1)带负号;当jijjn为偶排列时(1)带正号;Fs2.3n阶行列式
§2.3 n阶行列式 3. n 级行列式 等于所有取自不同行不同列的 n 个元素的乘积 (1) 每一项(1)都按下列规则带有符号: 11 12 1 21 22 2 1 2 n n n n nn a a a a a a a a a 1 2 1 2 n j j nj a a a 当 j j j 1 2 n 为奇排列时(1)带负号; 当 j j j 1 2 n 为偶排列时(1)带正号; n 级行列式 的代数和,这里 为 的排列. 1 2 n j j j 1,2, ,n

即ain aiz .. aina2i a22 ... a2nE (-1)(i-n) au;2im.ji.jnani an "..annZ表示对所有1、2、….、n的n级排列求和这里jii..jnF82.3n阶行列式
§2.3 n阶行列式 即 1 1 2 1 2 11 12 1 ( ) 21 22 2 1 2 1 2 ( 1) n n n n j j n j j nj j j j n n nn a a a a a a a a a a a a = − 这里 表示对所有1、2、… 、 n的n级排列求和. 1 2 n j j j

注:au a ... ara21 a22 *.. a2n1)行列式常简记为det(a)或ailan an.... an011主对角线副对角线ar.aa21 a22a2n2) D=中的数称为行列式D处于Ani anz... amn第i行第i列的元素,i称为行指标,i称为列指标3)n级行列式定义展开式中共有n!项Fs2.3n阶行列式
§2.3 n阶行列式 2) 中的数 称为行列式D处于 11 12 1 21 22 2 1 2 n n n n nn a a a a a a D a a a = ij a 注: 第 i 行第 j 列的元素, i 称为行指标, j 称为列指标. 3) n级行列式定义展开式中共有n!项. 1) 行列式 常简记为 或 11 12 1 21 22 2 1 2 n n n n nn a a a a a a a a a det( )ij a . ij a 主对角线 副对角线

例1计算行列式= 2×(-3) -(-1)×4=-212332123=1+18 +12 -9 -4 -6 =121F82.3n阶行列式
§2.3 n阶行列式 例1 计算行列式 2 1 4 3 − − 1 2 3 2 1 3 3 2 1 − − ( 1) 4= −2 = 1 +18 +12 −9 −4 −6 = 12 = − 2 ( 3)
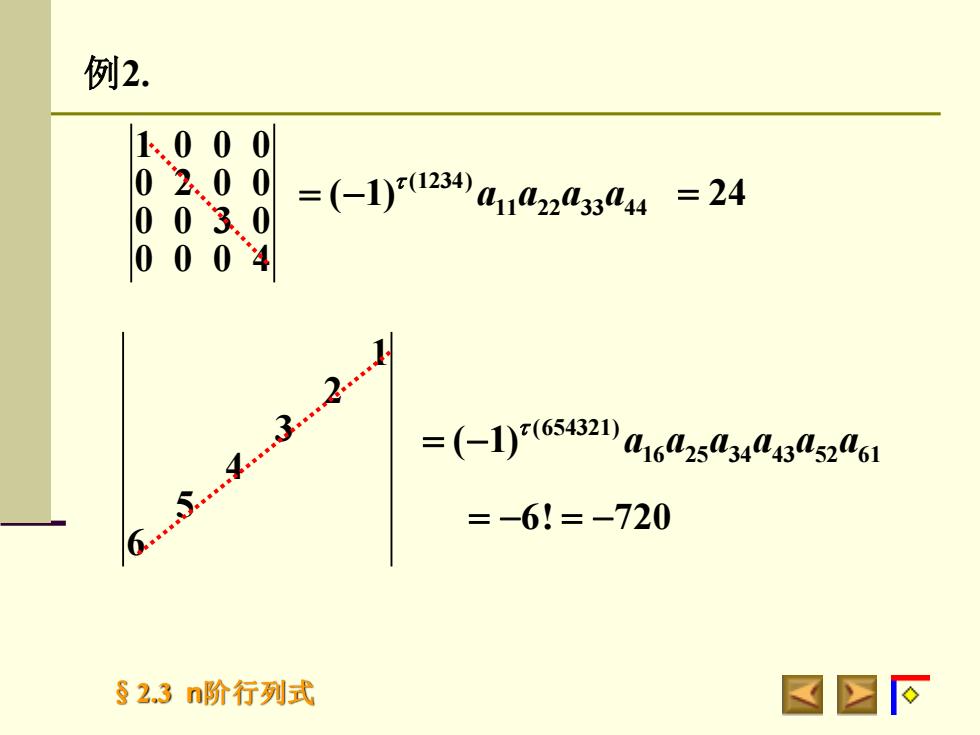
例2.1.0 0 002.00=(-1)(1234) a422433444 = 24003.100-1=(1)(654321)242= -6! = -720s2.3n阶行列式R
§2.3 n阶行列式 1 2 3 4 5 6 例2. 1 0 0 0 0 2 0 0 0 0 3 0 0 0 0 4 = −6! (1234) 11 22 33 44 ( 1) a a a a = − (654321) 16 25 34 43 52 61 ( 1) a a a a a a = − = 24 = −720

一般地,对角形行列式d.=dd,..d,3d.n(n-1)dn2=(-1)d,d,...dd.区s2.3n阶行列式
§2.3 n阶行列式 一般地, 1 ( 1) 2 2 1 2 ( 1) n n n n d d d d d d − = − 1 2 1 2 n n d d d d d d = 对角形行列式