
西安毛子科技大学数学与统计学院XIDIAN UNIVERSITYSchool of mathematies and statisties高等数学第一节导数概念
第一节 导数概念
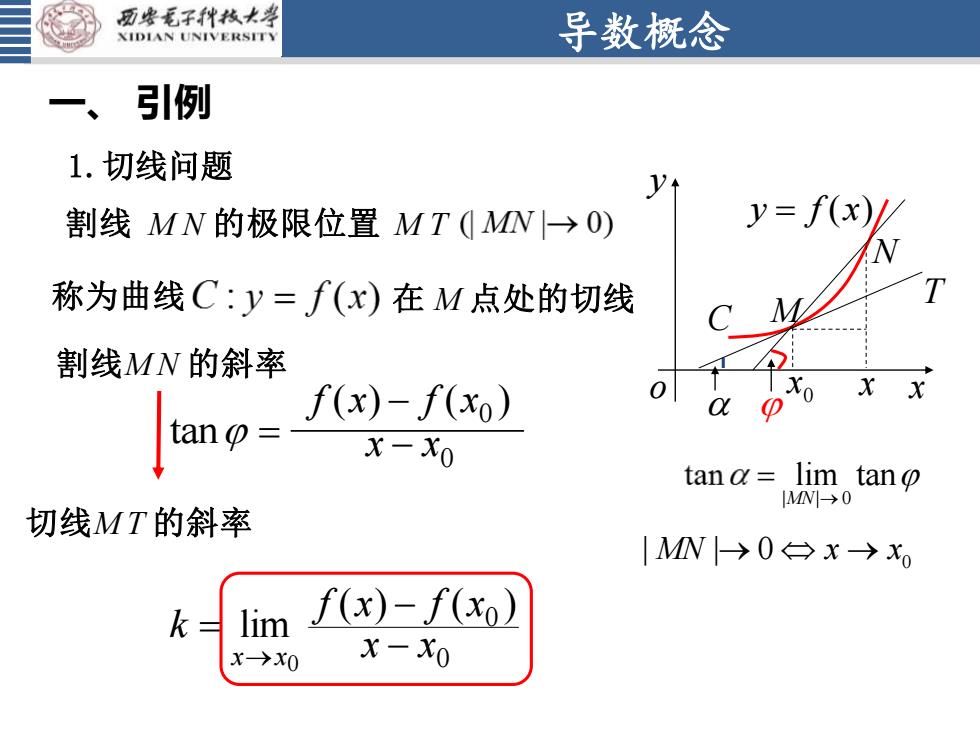
西安毛子科技大学导数概念XIDIAN UNIVERSITY一、 引例1.切线问题Vy= f(x)/割线MN的极限位置MT(MN→O)T称为曲线C:y= f(x)在M点处的切线C割线MN的斜率xx0X0f(x)- f(xo)αDtan @ =x-Xotan α = lim, tan g[MN)→0切线MT的斜率IMN→0x→xf(x)- f(xo)limk=x-Xox→xo
导数概念 1.切线问题 x y o y = f (x) C N T 0 x M x 称为曲线 在 M 点处的切线 割线 M N 的极限位置 M T 割线M N 的斜率 tan = ( ) ( ) 0 f x − f x 0 x − x 切线M T 的斜率 lim 0 x x k → = ( ) ( ) 0 f x − f x 0 x − x | | 0 lim tan MN → = 一、 引例 0 | | 0 MN x x → →

西要毛子科技大学导数概念XIDIANUNIVERSITY2.变速直线运动的瞬时速度问题设质点运动的位置函数是s=f(t),则to到t的平均速度为f(t)- f(to)1t-to在t。时刻的瞬时速度定义为f(to)f()f(t)- f(to)slimV=0ttot-to>to
导数概念 2.变速直线运动的瞬时速度问题 s o 0 t ( ) 0 f t f (t) t 设质点运动的位置函数是 则 到 的平均速度为 v = ( ) ( ) 0 f t − f t 0 t − t 在 时刻的瞬时速度定义为 lim 0 t t v → = ( ) ( ) 0 f t − f t 0 t − t

西安毛子科技大学导数概念XIDIAN UNIVERSITSf(t)- f(to)f(x)-f(x)瞬时速度 v=lim切线斜率k=limt-tot→>toX-→>XoX-Xo共性:所求量为函数增量与自变量增量之比的极限加速度变化率问题是速度增量与时间增量之比的极限角速度是转角增量与时间增量之比的极限线密度是质量增量与长度增量之比的极限电流强度是电量增量与时间增量之比的极限
导数概念 切线斜率 瞬时速度 0 0 0 ( ) ( ) lim t t f t f t v → t t − = 0 − 0 0 ( ) ( ) lim , x x f x f x k → x x − = − 共性: 所求量为函数增量与自变量增量之比的极限 加速度 角速度 线密度 电流强度 是速度增量与时间增量之比的极限 是转角增量与时间增量之比的极限 是质量增量与长度增量之比的极限 是电量增量与时间增量之比的极限 变 化 率 问 题

西安毛子科技大学导数概念IDIAN UNIVERSITY函数在一点处的导数的定义定义1设函数=f(αx)在点。的某邻域内有定义,()-(x)存在,则称函数f()在点处可导,若 limx->x0x-Xo并称此极限为y=f(x)在点x。的导数df(x)dy记作:;f(x);dxdxx=XoAyf(x)- f(xo)x= = f(x) = lim即limAx-0 △x-xoX-Xof(x +Ar)-f(x)- 1f(xo +h)-f(x)Jim= limh△xh->0△x-0
导数概念 二、 函数在一点处的导数的定义 0 lim x x → 0 0 f x f x ( ) ( ) x x − − 若 存在, 定义1 设函数 在点 的某邻域内有定义, 则称函数 在点 处可导, 并称此极限为 在点 的导数. 记作: 0 ; x x y = 0 f x ( ) ; 0 d ( ) d f x x x x = 0 d ; d x x y x = 0 lim x y → x = 即 0 x x y = 0 = f x ( ) 0 0 0 lim ( ) ( ) x x f x f x → x x = − −

西安毛子科技大学导数概念XIDIANUNIVERSITYf(x)-f(xo)Ay定义2若极限limlim不存在,x->Xox-xoAx-0 △x则称函数f(x)在点 x不可导Ay特别地,若lim:80,也称 f(x)在α的导数为无穷大Ax-0 △x
导数概念 特别地,若 0 lim , x y → x = 也称 在 的导数为无穷大. 定义2 若极限 不存在, 则称函数 在点 x0 不可导

西要毛子科技大学导数概念XIDIAN UNIVERSITYf(x +△x)- f(x)f(x)-f(x)R5f'(x)= lim :lim左导数AxAx->0x→>x0x-Xof(xo +△x)- f(xo)f(x)- f(xo)f'(x)= lim lim右导数AxAr->0x-→>xox-Xo定理1函数y=f(x)在点x。可导的充分必要条件是f(x)与 f(x)存在且相等,即f'(xo)存在f'(x)=f'(xo)
导数概念 左导数 右导数 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ) lim lim x x x f x x f x f x f x f x x x x − − → → + − − = = − - 即 定理1 函数 在点 可导的充分必要条件是 + + 0 0 0 0 + 0 0 0 ( ) ( ) ( ) ( ) ( ) lim lim x x x f x x f x f x f x f x → → x x x + − − = = − 0 f x ( ) 存在 与 存在且相等

西安毛子科技大学导数概念XIDIANUNIVERSITS例1.证明函数f()=|x|在x=0 不可导证: (0+h)-T(0)[ h|hhI h|-hf(0) = limlim1hhh→>0-h-→>0-f(0) =1f'(0) # f(0)所以 f(x)=|x|在x=0 不可导
导数概念 例1. 证明函数 在 x = 0 不可导. 证: f h f (0 ) (0) h + − | | h h = 0 0 | | (0) lim lim h h h h f h h − → → − − − = = = −1 f (0) 1 + = f f (0) (0) − + 所以 在 x = 0 不可导

西安毛子科技大学导数概念XIDIANUNIVERSITY三、 利用函数在一点的导数的定义求极限f(x +△x)- f(x)f(x)-f(x) = lim f'(xo)= lim Ar→>0Axx-→>x0x-Xo例2设f'(x)存在,求下列极限f(xo -2h)-f(xo)(I) I =limhh->0f(x-2h)- f(xo).(-2) =-2 f(xo)解I=lim-2hh->0
导数概念 三、 利用函数在一点的导数的定义求极限 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ) lim lim x x x f x f x f x x f x f x → → x x x − + − = = − 例2 设 0 f x ( ) 存在,求下列极限 0 0 1 0 ( 2 ) ( ) (1) limh f x h f x I → h − − = 解 0 0 1 0 ( 2 ) ( ) lim ( 2) h 2 f x h f x I → h − − = − − 0 = −2 ( ) f x

西安毛子科技大学导数概念XIDIAN UNIVERSITY例2设f(x)存在,求下列极限(2) I, = limh2[f(x +f(x))2h?[f(xf(xo))[f(xF(xo))2h?解 I,=limlim112h->00h-→>00h22h?Cx
导数概念 解 0 1 ( ) 2 f x + = 2 2 0 0 2 1 (2) lim [ ( ) ( )] h 2 I h f x f x → h = + −0 1 ( ) 2 = f x 0 0 2 2 2 1 [ ( ) ( )] 2 lim h 1 f x f x h I h → + − = 0 0 2 2 1 [ ( ) ( )] 1 2 lim 2 1 2 h f x f x h h → + − = 例2 设 0 f x ( ) 存在,求下列极限