
西安毛子科技大学数学与统计学院XIDIAN UNIVERSITYSchool of mathenmnties and sttisties雷等数学第五节函数的微分
第五节 函数的微分

西安毛子科技大学函数的微分XIDIAN UNIVERSITY一、微分的概念引例一块正方形金属薄片受温度变化的影响,其边长由x变到x+△x,问此薄片面积A改变了多少?解当 x在x取得增量△x 时,面积的增量为XoArA =(x。 + Ax)? - x(△x)2Ax= 2xAx +(Ax)3XoAr关于△x的 △x→0 时为△xA=x-Xo线性函数?的高阶无穷小
函数的微分 一、微分的概念 0 x x 面积的增量为 0 x x 2 0 A = x 0 x x 2 ( ) x 当 x 在 x0 取 得增量 x 时, 引例 一块正方形金属薄片受温度变化的影响, x0 变到 x x 0 + , 问此薄片面积 A 改变了多少? 其边长由 解 的高阶无穷小 关于 的 →x 0 时为 x 线性函数 x

西安毛子科技大学函数的微分XIDIANUNIVERSITY定义1若函数 y=f(αx)在点 x的增量可表示为Ay = f(x +△r)- f(x) = A△x+o(△x)(A为不依赖于△x的常数)则称函数 = f(x)在点 x。可微,而 A△x称为f(x)在点xo的微分,记作dy或df(x),即dy = Ax
函数的微分 而 A x 称为 在点 的微分,记作 或 即 dy A x = = + A x o x ( ) 则称函数 y f x = ( ) 在点 可微, 定义1 若函数 在点 x0 的增量可表示为 ( A 为不依赖于 的的常数)

西安毛子科技大学函数的微分XIDIAN UNIVERSITY理论上,利用定义完全可以检验函数在一点是否可微如 =x,Ay=(x +Ax)-x =3xAx +3x (Ax)* +(Ax)3关于Ax的r→0时为△r线性主部的高阶无穷小故y=x在其定义域内的每一点xo处都可微,且dy=3x△x但实际中,用定义判断函数在一点是否可微往往比较繁琐xAx如 y= sin x, Ay= sin(xo +△x)-sin X=2cosX +sin22有没有判定函数在一点可微行之有效的简便方法呢?
函数的微分 理论上,利用定义完全可以检验函数在一点是否可微. 但实际中,用定义判断函数在一点是否可微往往比较繁琐. 3 3 3 2 2 3 0 0 0 0 如 y x y x x x x x x x x = = + − = + + , ( ) 3 3 ( ) ( ) 关于 x 的 线性主部 故 在其定义域内的每一点 处都可微,且 3 y x = 0 x 2 0 d 3 . y x x = 如 0 0 0 sin sin( ) sin 2cos sin . 2 2 x x y x y x x x x = = + − = + , 有没有判定函数在一点可微行之有效的简便方法呢? 0 x x y = 的高阶无穷小 →x 0 时为 x

西安毛子科技大学函数的微分XIDIANUNIVERSITY定理函数y=f(x)在点x可微的充分必要条件是y=f(x)在点x可导,且A=f(x),即dy = f(xo)Ax证(必要性)已知y=f(x)在点x可微,则Ay = AAx + o(Ax)上式两边除以x,当△x→0时,0(△x)AylimlimA+即 f(x)=AAAr-0AxAr-A(Ax故y=f(x)在点x可导,且A=f'(x)
函数的微分 0 d ( ) . y f x x = 证 (必要性)已知 y f x = ( ) 在点 x0 可微,则 故y f x = ( )在点 x0 可导,且 A f x = ( )0 . 0 0 ( ) lim lim x x y o x A A → → x x = + = 上式两边除以 , x 当 →x 0 时, 0 即 ( ) f x A = = + y A x o x ( ). 定理 函数 y f x = ( ) 在点 x0 可微的充分必要条件是 y f x = ( ) 在 0 点 x 可导,且 A f x = ( )0 ,即

西安毛子科技大学函数的微分XIDIAN UNIVERSITY定理 函数= f(x)在点x可微的充分必要条件是 y= f(x)在点可导,且A=f(x),即dy = f'(xo)Ax证(充分性)已知y=f(x)在点x可导,则=f(x)= f(x)+α (limα=0)lim Ar-0 △xf'(x)= A,故 △y= f'(x)△x+α△x = A △x + o(△x)α△x = o(△x)即y=f(x)在点xo可微,且dy=f(x)Ax
函数的微分 证 (充分性)已知 y f x = ( ) 在点 x0 可导,则 0 0 lim ( ) x y f x → x = 0 0 ( ) (lim 0) x y f x x → = + = 即 y f x = ( ) 在点 x0 可微,且 d ( ) y f x x = 0 . 故 0 ( ) , ( ). f x A x o x = = 0 ( ) = + y f x x x = + ( ) A x o x 0 d ( ) . y f x x = 定理 函数 y f x = ( ) 在点 x0 可微的充分必要条件是 y f x = ( ) 在 0 点 x 可导,且 A f x = ( )0 ,即

西安毛子科技大学函数的微分XIDIANUNIVERSITY注(1)定理表明,若f(x)存在,则Ay= f(x)Ax +o(Ax) 且 dy = f'(x)Ax(2)当f(x)±0时,有AyAy = limy=1lim1mAx=0 dy - Ar-0 f(x0)Axf(xo) Ar-=0 △x从而,当△x一→0时,△y与dy是等价无穷小,换言之,即Ay= dy + o(dy)故当Ax很小时,有近似等式△y~dy
函数的微分 0 = + y f x x o x ( ) ( ) 且 0 d ( ) . y f x x = 0 0 0 0 0 1 lim lim lim 1. d ( ) ( ) x x x y y y → → → y f x x f x x = = = 0 (2)当 f x ( ) 0 时,有 从而,当 →x 0 时, y 与 dy 是等价无穷小,换言之,即 = + y y o y d (d ) 故当 x 很小时,有近似等式 y yd .. 注 (1)定理表明,若 f x ( )0 存在,则

西安毛子科技大学函数的微分XIDIAN UNIVERSITY定义2函数y=f(x)在任意点x的微分,称为函数的微分记作dy或df(x),即dy = f(x)Ax规定:△x=dx.于是函数 =f(x)的微分又可记作dy= f'(x)dxdy导数也叫做“微商= f'(x)从而有dx这表明,函数的导数就是函数的微分dy与自变量微分dx之商
函数的微分 d ( ) . y f x x = d ( )d y f x x = 从而有 d ( ) d y f x x = 这表明,函数的导数就是函数的微分 dy 与自变量微分 dx 之商. 函数 y f x = ( ) 在任意点 x 的微分,称为函数的微分, 规定: d . =x x 于是函数 y f x = ( ) 的微分又可记作 定义2 记作 dy 或 d ( ) f x ,即
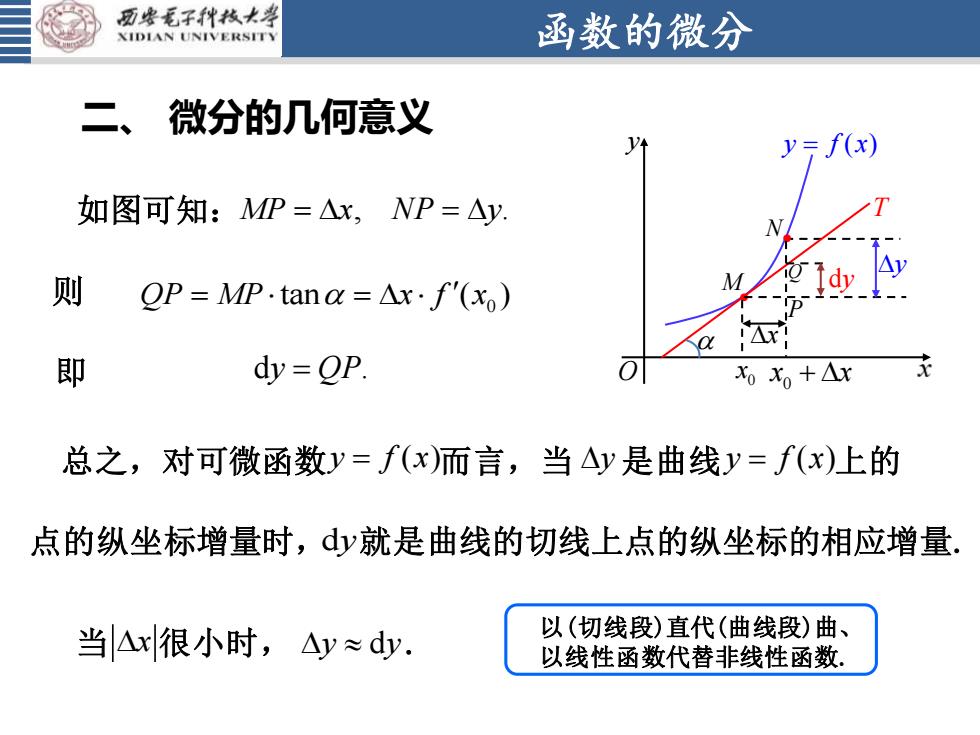
西安毛子科技大学函数的微分XIDIANUNIVERSITY二、 微分的几何意义y= f(x)yt如图可知:MP=△x,NP=AyA1M则QP = MP.tanα = x · f'(x):Ax!Ody = QP.即可Xo X+Ax总之,对可微函数y=f(x)而言,当△y是曲线y=f(x)上的点的纵坐标增量时,dy就是曲线的切线上点的纵坐标的相应增量以(切线段)直代(曲线段)曲当Ax很小时,Ay~dy。以线性函数代替非线性函数
函数的微分 二、 微分的几何意义 如图可知: d . y QP = MP x = , NP y = . 0 则 QP MP x f x = = tan ( ) 即 yO y f x = ( ) • M N • x Ty dy PQ 当 x 很小时, y yd . 以(切线段)直代(曲线段)曲、 以线性函数代替非线性函数. 总之,对可微函数 y f x = ( ) 而言,当 y 是曲线 y f x = ( ) 上的 点的纵坐标增量时, dy 就是曲线的切线上点的纵坐标的相应增量. 0 x0 x x +

西安毛子科技大学函数的微分XIDIANUNIVERSITY三、基本初等函数的微分公式与微分运算法则1:基本初等函数的微分公式由可微函数的微分表达式dy= f'(x)dx可见,利用每一个基本初等函数的导数公式,即可相应的写出基本初等函数的微分公式(见教材P113-114表格),这里省略例如:d(x")=μuxu-'dx,d(a")=a"lnadx 等等
函数的微分 三、基本初等函数的微分公式与微分运算法则 1. 基本初等函数的微分公式 由可微函数的微分表达式 可见,利用每一个基本初等函数的导数公式,即可相应的写 出基本初等函数的微分公式(见教材P113-114表格),这里省略. 例如: d( )= ln d x x a a a x 1 d( )= d x x x − , 等等. d ( )d y f x x =