
西安毛子科技大学数学与统计学院School of mathematies and statistiesXIDIAN UNIVERSITY西等数学第九节闲区间上连续函数的性质
第九节 闭区间上连续函数的性质

西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY一、最大最小值定理1.定义f(x)是定义在区间I上的函数,如果 日x。EI,使得对于xI,都有f(x)≤f(x) (f(x)≥f(x)则称f(x)是函数在区间I上的最大值(最小值)
闭区间上连续函数的性质 1. 定义 一、最大最小值定理 对于 都有 (最小值). 是定义在区间 上的函数,如果 使得 则称 是函数在区间 上的最大值
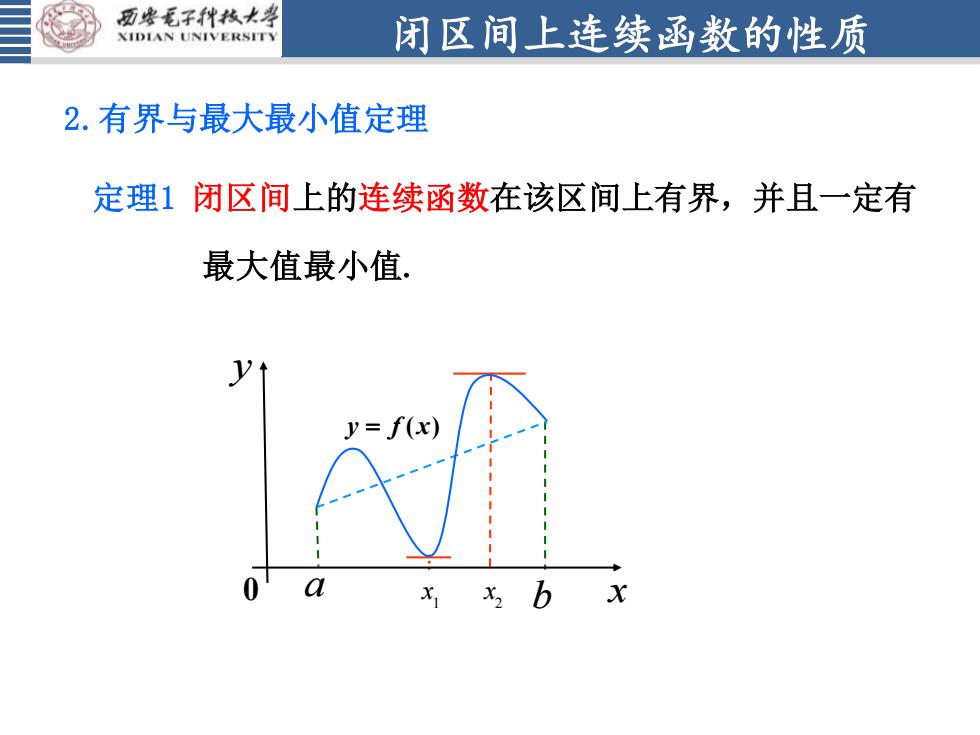
西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY2.有界与最大最小值定理定理1闭区间上的连续函数在该区间上有界,并且一定有最大值最小值山f(x)0abxxX2
闭区间上连续函数的性质 定理1 闭区间上的连续函数在该区间上有界,并且一定有 2.有界与最大最小值定理 最大值最小值. 1 x 2 x y = f (x) a 0 b x y

西安毛子科技大学闭区间上连续函数的性质XIDIANUNIVERSIT注若定理条件不满足,即函数在开区间上连续,或在闭区间内有间断点,定理的结论不一定成立2例如y=x,xE(O,1)无最大值和最小值在[0,2]上也[-x+1, 0≤x<1例如1, x=1f(x)=无最大值和-x+3, 1<x≤2最小值.元元例如 =tanx在开区间(-连续,但没有界22[1x+0例如V=x在闭区间[-1,1] 不连续,无界0x=0
闭区间上连续函数的性质 无最大值和最小值. o x y 1 1 x o y 1 1 2 2 在[0,2]上也 无最大值和 最小值. 注 若定理条件不满足,即函数在开区间上连续,或在闭区 间内有间断点,定理的结论不一定成立. 例如 在开区间 连续,但没有界. 例如 例如 例如 在闭区间 不连续,无界

西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY三、零点定理1.定义如果存在x使得f(α)=0,则x称为函数f(α)的零点x。为函数 f(x)的零点<> x。为方程f(x)=0的根>曲线y=f(x)与x轴有交点
闭区间上连续函数的性质 三、零点定理 如果存在 使得 ,则 称为函数 的零点. 1. 定义 为函数 的零点 为方程 的根. 曲线 y f x x = ( ) 与 轴有交点

西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY2.零点定理定理2 设 f(x)C[a,b] 且 f(a)·f(b)<0,那么至少有一点号e(a,b),使f()=0,即方程f(x)=0在(a,b)内至少存在一个实根.(证明略)yf(b)Ca0b中5f(a)
闭区间上连续函数的性质 定理2 那么至少有一点 使 (证明略) 2.零点定理 设 且 即方程 在 内至少存在一个实根. C 0 f a( ) f b( ) a b x y

西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY四、介值定理定理3 设 f(x)C[a,b]且f(a)= A,f(b)=B, A B,则对 A 与 B之间的任一数 C,至少有一点 E(a,b),使f() =C.证 作辅助函数(x)=f(x)-C,则 (x)C[a,b],且P(a)p(b) =(A-C)(B -C) < 0故由零点定理知,至少有一点 E(a,b)使 ()=0即f() = C.推论在闭区间上的连续函数必取得介于最小值与最大值之间的任何值
闭区间上连续函数的性质 定理3 设 且 A 与 B 之间的任一数 C , 一点 证 作辅助函数 则 且 故由零点定理知,至少有一点 使 即 则对 至少有 使 四、介值定理 推论 在闭区间上的连续函数必取得介于最小值与最大值 之间的任何值

西安毛子科技大学闭区间上连续函数的性质IDIANUNIVERSITY例1.证明方程x2 -4x2+1=0在区间(0,1)内至少有一个根,又证: 显然 f(x)=x-4x2 +1eC[0,1],f(0)=1>0,f(1)=-2<0故据零点定理,至少存在一点 ≤E(O,1),使 f()=0,即3-45+1=0即方程 x3 -4x2+1=0 在区间(0,1)内至少有一个根
闭区间上连续函数的性质 例1. 证明方程 证: 显然 又 故据零点定理, 至少存在一点 使 即 在区间 内至少有一个根. 即方程 在区间 内至少有一个根

西安毛子科技大学闭区间上连续函数的性质XIDIAN UNIVERSITY例2.证明方程x=asinx+b,α>0,b>0,至少有一个不超过a+b的正根.证:设f(x)=x-asinx-b,则(x)在[0,a+b)上连续.且 f(0)=-b0由零点定理,至少3E(O,α+b),使f()=0综上,方程x=asinx+b至少有一个不超过a+b的正根
闭区间上连续函数的性质 例2. x a x b a b sin , 0, 0, a b = + + 证明方程 至少有一个不超过 的正根. 设 f x x a x b ( ) sin , = − − 则f x a b ( ) [0, ] 在 + 上连续. 且 f b (0) 0, = − f a b a a b ( ) [1 sin( )] 0 + = − + 1 ( ) 0, 若f a b a b + = = + 则 是方程的根. 2 ( ) 0, ( ) 0 若f a b f a b + + 则 由零点定理,至少 + = (0, ) ( ) 0. a b f ,使 综上,方程x a x b a b = + + sin 至少有一个不超过 的正根. 证:

西安毛子科技大学闭区间上连续函数的性质KIDIANUNIVERSIT例3设函数f(α)在[0,1]上连续,且f(0)=f(1),证明至少[0,1],使得 ()=f(+)12证 令(x)=f(x)-f(x+),则 (x) =C[0,三)且 (0)= f(0)-()), ()=f()-f()=f()-f(0),即(0)p()≤0,(1)若(0)()=0,取=0或者=一即可。2(2)若 (0)g()<0,由零点定理知至少有一点 (0,) [0,1], 使 ()=0, 即 f(5)=F(+
闭区间上连续函数的性质 例3 设函数 在 上连续,且 证明 至少 使得 证 令 则 且 即 由零点定理知至少有一点 使 即 (1) 若 取 或者 即可. (2) 若