
第十章重积分 本章和下一章是多元函数积分学的内容,在一元函数积分学中我们学习了不定积分和定积 分,同时我们也知道定积分是某种形式的和的极限,这种和的极限推广到定义在区域、曲线 和曲面上就是重积分、曲钱积分和曲面积分的概念。本章我们将介绍重积分(二重积分、三 重积分)的概念、计算方法以及他们的一些应用。 $1、二重积分的概念 一、二重积分的概念 1、引例与定义 (1)曲顶柱体的体积 设函数z=fx,),当(化y)∈D时,f(x,)20,且fx,)在D上连续。由曲面z=f(x,y)、 xy平而的区城D、母线平行于z轴的柱面所围成的空间区域称为曲顶柱体,或称为以曲面 z=x,)为顶,以平面区城D为底,母线平行于2轴的曲顶柱体。 2=f(x,y) 已知:平顶柱体的体积=底面积×高 3,-f59,) ①分割:用平面曲线网将区城D分割为 A0,A02,·,A0,,A0。 相应地将曲顶柱体分割为n个小的曲顶柱体: AK,AV,...Av,...Av 其中△y表示第i个小曲顶柱体、也表示该柱体的体积,则:V=∑A: ②速V的近似值:(,n,)∈△g,△V≈f5,n,)△g(i=L,2,,n):故 V-2a业*2f5nAa (5,7) ③垡业的指确值:记=max所有△a,的直径倒,则,V=im∑f(乐,n)△a,: (2)平面薄板的质量问题 设平面薄板占有xOy平面上的区城D,密度函数为p=p(x,y),当(x,)eD时,p(x,)>0 且在D上连续。 同理可得,质量计其公式:m=m∑p(,n)△a,:
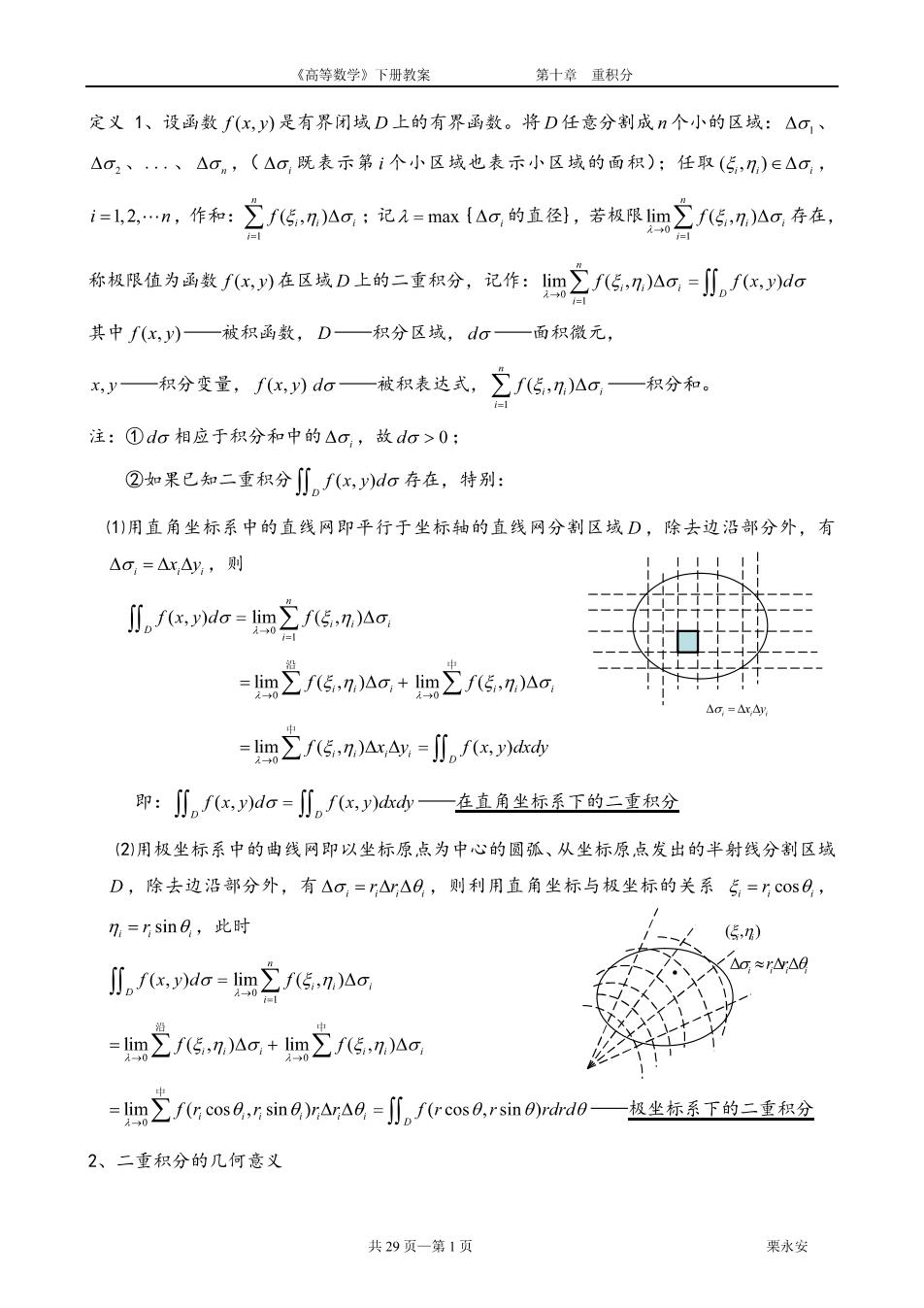
《高等数学》下册教案 第十章重积分 定义1、设函数∫(x,y)是有界闭域D上的有界函数。将D任意分割成n个小的区域:△口、 △、、△,((△G,既表示第i个小区域也表示小区域的面积):任取(⑤,)∈△, i=l,2,作和:之fG,na,:记=mmx△a,的直,若极限m之f八5,nAa,存在, 称极限值为函数f(x,)在区城D上的二重积分,记作:Iim∑f5,n,)△o,=川nfx,y)do 其中f(x,)—被积函数,D—积分区域,do—面积微元, xy—积分变量,f,)da—被积表达式,f八5,n)a,一积分和。 注:①do相应于积分和中的△a,故do>0: ②如果已知二重积分儿nx,)do存在,特别: (1)用直角坐标系中的直线网即平行于坐标的直线网分割区城D,除去边沿部分外,有 Ao,=AxAy,则 ∬。fxo=m2fG,n)Aa -im()Ao,+lim()Ao 4g=44y =lm∑f5,n)Ax4y=∬nfx,dhd 即:川nx,y)do=川nfx,y)kd一在直角坐标系下的二重积分 2)用极坐标系中的曲线网即以坐标原点为中心的圆孤、从坐标原点发出的半射线分割区城 D,除去边沿部分外,有△a,=r△△日,则利用直角坐标与极坐标的关系5=rcOs日, 7,=5sin日,此时 (ξ) (x.yda-lim()Ao △o≈rW△8 =m∑f5,n)Ao,+mΣfGn,)Aa, =lim∑f(cos6,rsin8)rAyA6=j∬nf(cos0,rsin0)rdd0一极坐标系下的二重积分 2、二重积分的几何意义 共29页一第1页 果水安

《高等数学》下册教案 第十章重积分 1)当fk,)之0川。fx,dG的几何意义表示以区城D为底,以曲面2=fx,)为顶,母线 平行于:轴的曲顶柱体体积(位于x0y上方): 2若化,川≡l,八nfx,da=川ndG积分值等于区城D的面积。 注:①fx,y)≤0时,nfx,y)do的几何意义表示以区拔D为底,以曲面z=fx,)为顶 母线平行于:轴的曲顶柱体的体积: ②若积分区域D关于x轴对称,D,是位于x轴上侧的一半区域 。fk.wo=2 f(,yda f(s.y=)f,- 0 f(x,)=-f(x,-y) ③设积分区域D关于y轴对称,D,是位于y轴右侧的一半区域,则 fr.yda-2 a f- 0 f(x,y)=-f(-x,y) 例1、根据二重积分的几何意义,指出下列积分值,其中D:x2+y2≤R2, D,:x+ys1,x≥0,y≥0:∬R2-x-yda,∬da,j∬0-x-to。 解:∬o=D的面积=xR:八R-r-少do=上丰球体体积=子xR 0--o=四面体的体积-名 例2、指出下列积分值,川(2-2+y)d6,其中D:x2+y2≤4。 解:被积函数2=2-√+少≥0,(化,)∈D,根据二重积分的几何意义,积分值等于以曲面 z=2-√2+y2为顶,以D:x2+y2≤4为底的曲顶柱体的体,即等于底半径为2,高为2 2-F+aa2y2- 例3、指出下列积分值,其中其中D:x+y10 ∬。xF+rda f∬n3-x2 sin xy)do 解:川nxVF+ydo=0 共29页一第2页 果水安

《高等数学》下册教案 第十章重积分 川n6-sin xyda=3go-j。sin xyda=3-0023=60 二、二重积分的性质 可以证明,连续的函数一定可积,以下总假设二重积分存在。 性质1、川nfx,y)do=nf(x,y)do,k为非零常数: 性质2、∬n/x,)gxdg=川。fx,do±川。gxda: 性质3、若D=D,+D,且D∩D,=(除边沿部分外),则 ∬nfx,dg=。fcdg+∬nfx,do 性质4(保序性)、若fx川≥gx,川,(x,)∈D,剥:川。fx)do≥川。g(xo: 表明,当积分区域相同时,被积函数越大,则积分值越大,可以依据此性质比较两个积分值 的大小。 特例:(1)若fx)20,(x,)∈D,则∬nfx,y)do≥0: 21∬(das∬lfx,川da 其中2)几何意义在于:左端—体积的代数和,右端—体积。 性质5、(估值定理)若m≤fx,)≤M,(c,)∈D,则 mc≤∬nf,y)do≤Ma (g是D的面积) 注:利用此性质可以估计积分值的范围。 性质6、(中值定理)若f(x,y)在有界闭区域D上连续,则存在(⑤,)∈D,使得: ∬nfx,y)do=f(5,n)o(o是D的面积) 证明:因为f(x,)在有界闭区域D上连续,则在D上可以取得最大、最小值M与m,即 m≤fx,)≤M,(xy)∈D;根据性质4, 八。mda≤j。fx,dos∬。Mia 即mo≤川nf心,o≤Mo,浅m≤号川。fdo≤M,由闭区城上连续画数的性质,存在 (传,eD,使得f5,0=号。fxdo,即:广。fx,da=f5,0a 例4、比较积分∬。(x+dg与川。x+do的大小,D由(x-2)+0-)=2围成的圆城。 共29页一第3页 果水安
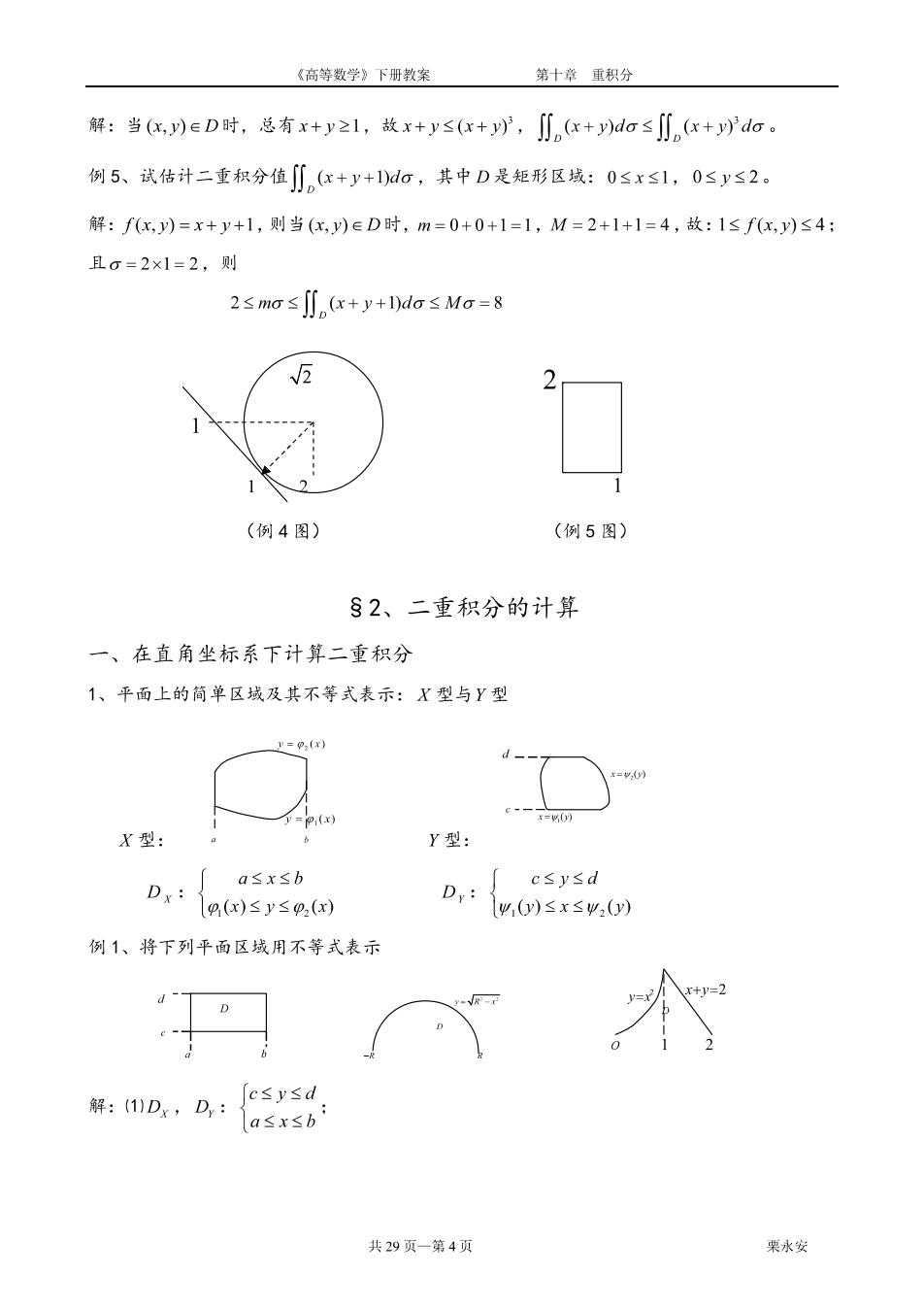
《高等数学》下册教案 第十章重积分 解:当(x,)eD时,总有x+y之1,故x+y≤(x+y,∬x+do≤川x+ydc。 例5、试估计二重积分值川x+y+1)do,其中D是矩形区城:0≤x≤1,0≤y≤2。 解:fx,)=x+y+1,则当(化,y)∈D时,m=0+0+1=1,M=2+1+1=4,故:1≤fxy)≤4: 且0=2×1=2,则 2≤mo≤,(x+y+I)do≤Ma=8 (例4图) (例5图) §2、二重积分的计算 一、在直角坐标系下计算二重积分 1、平面上的简单区域及其不等式表示:X型与Y型 =0 X型: Y型: a≤x≤b 「c≤y≤d D:sy D,:{,0sx5w.0 例1、将下列平面区城用不等式表示 g- 解:1D,D,:Cyd a≤xsb 共29页一第4页 果水安

《高等数学》下册教案 第十章重积分 -R≤xSR 0≤y≤R 2)Dx: 0≤y≤VR2-x D:R-ysys-yi 3)Dx: 「0sys1 及0≤,2-:D:{55x2-y 2、在直角坐标系下二重积分的计算 例1、计算曲顶柱体的体积V=川nfx,y)do,f(x,)20。 解:设曲顶柱体的底为x0y平面上的区域D,顶为曲面z=f(x,)20:设区城D为X型区域 且D: 「a≤x≤b (9)≤y≤g,(x) x,∈[a,,过x点作垂直于x轴的平面 平面与曲顶柱体有一截面,设数面面积为A(x), 则4,)为:40)=∫6: y=g(x) 由x∈[a,的任意性,有x∈[a,创,我面面积为:Ax)=∫%fx,)d 根据平行截面面积已知立体体积的计算公式,曲顶柱体的体积为 vds 从而,川。f化,dg=业=红)本二次积分(累次积分) 注:①对于一般的二重积分川nfx,y)do,若其积分区城D为X型区城,即D: ass只.剥也有:fdo=fdh: [asx≤b 为了书写方便,二次积分常写为: 。f,do=jmfd=fx4 csysd ②同理,若积分区装D为y型区城,即D:{05:,的则有 dadyds ③如果积分区城不是简单区域,则应当适当划分为简单区城再逐个积分。 共29页一第5页 果水安

《高等数学》下册教案 第十章重积分 例2、计算二重积分川。3do,其中积分区城D为矩形:≤x≤h (csysd' 解:根据上面的讨论,视D为X型区摄,D:a≤x≤B lesysd”则 ∬ndo∫d=)d2-cd=子62-ad-c=jw 特例:若积分区城D为矩形区城D:口5x5办.被积禹教恰好可以写为,)=不W6。 lc≤ysd' 则∬。0do=fx∫0。 例3、计算积分川3x2ydo,其中D由曲线x=y2-1与x-y=1围成。 y+1 解:1视D为y型域,则D:-13xSy+1 ∫-1≤y≤2 2 ∬n3xdo=」时3x=∫3x =∫yx本=∫0+-02-y -io4r-o4hG2-d02-0 =0+-0w呢其cr-呢-9 2视D为X型城,则D: 15x0及{0x3 -x+l≤y≤+1x-1≤x≤Vx+ 川3xdo=小3do+。3xdo=j3x+3xd -3rw+3xw-3rr 引x1--达-器 例4、计算积分川nxV2+ydG,D由y=a-x2与y=0围成。 -a≤x≤a a 共29页一第6页 果水安

《高等数学》下册教案 第十章重积分 。xVR+rdo=FxP+y= 0≤x≤a :{--55-可.则 儿F+o广F+F-a-0 例5、计算积分川neda,D由x=2、y=x及x轴国成 所DxD:852为 edoe-ieai-ieie-f生 多D有r线n: 川nedc=eh此积分无法用牛顿莱布尼滋公式计算 注:以上例题表明,在直角坐标系下计算二重积分时,应注意积分顺序的选择,二重积分计 算的关键是转化为二次积分。 例6、将二重积分1=川。f化,y)o化为直角坐标系下的两种不同顺序的二次积分,其中D由 直线y=x、y=2x及y=2图成。 2 2 所a::{a品4 x≤ys2' 1=f,1=∫f+fx 例7改变二次积分1=层k,达的积分顺序。 解:由条件可得:D: 少≤r≤学,则积分区战为: 0≤y≤4 4信eh=cocg =f+fx, 共29页-第7页 果水安

《高等数学》下册教案 第十章重积分 例8、计算由平面x=0,y=0,x+y=1所围成的柱体被平面z=0以及抛物面x2+y2=6- 截得的立体的体权。 解:此立体为以D(由x=0,y=0,x+y=1围成)为底,以曲面 之6-x2-y z=6-x2-y2为顶的曲顶柱体,则 r=川6-2-yda=6o-j6。x2+yd x+y=1 =6号e0-+0-h=3-兮名 练习 1、将下面的二重积分∬nfx,y)do化为二次积分(两种顺序都要),其中积分区城D:①由 x+y=1、x=1及y=1国成:②由x=√R2-尸与y轴为成。 解:①。f(x.yda=∫fxd=jfc,d ②,在a小广-可fh 2、文换积分顺序:,k。 解:小Ff,t=f+。Ffx,t 3、计算积分川。+少-a,其中D由直线y=x、y=及x=2国成。 解:∬。r2+y2-do=∫x+y- +r贤r 192432313 244836 二、在极坐标系下二重积分的计算 1、极坐标系下的二重积分 (r,) 极坐标系下的坐标为:(,),与直角坐标的关系 r. =rm日0s052:极坐标系下的坐标南线: 〔x=rcos0 0 共29页一第8页 果水安

《高等数学》下册教案 第十章重积分 r=常数“以原点为中心的圆孤;日=常数一从原点发出的半射线 谈=重积分存在,则。x6=-之低,na: 用极坐标系中的曲线网分割区域D时,除去边沿部分外,均有: ag+ara0-a0 =2rw+(P1A0=22斯+1A0=2+G+1AA0=·wA0 考虑圆孤r=斤上的一点(G,0),取5=rcos6,n,=rsin瓦,则 ∬nfx,dg=m2f传,n)Aa,=m∑f5,mAa+∑fG,n)Aai =m∑可,7sm0raA0=(rcos0.rsin9dhd0 jj。fx,yda=J∬cos0,snd0 注:二重积分的面积微元do在极坐标系下为:do=rddB: 2、极坐标系下的简单区域 半射线日=日,与区域D边界曲线的交点不超过两个,则D为极坐标系下的简单区域。 「a≤0≤B 1)D: g(msrsp,(O则 ,fteasarsn0rti0-ajwesrsnt j∬f(co8,rsin8)rdd0=∫dog”f(rcos8,rsin8t ∫0≤0≤2m 3D:osrs 则 rsinOrdrdodosinrd -≤日≤& 4D:0≤rs9' 则 ∬nf0cos0,rsin0rdd0=∫dof(os0,rsin0)rh 共29页一第9页 果水安