
教 案 姓名冯增哲 2011-2012学年第二学期 时间节次 课程名称 高等数学 授课专业及层次 授课内容 微分方程的基本概念 可分离变量的微分方程 学时数 2学时 教学目的理解微分方程相关概念,掌握可分离变量的微分方程的解法 重 点微分方程的相关概念,可分离变量的微分方程的解法 难 点可分离变量的微分方程的解法 自学内容 《高等数学例题与习题》相关内容 使用教具多媒休 相关学科知识物理知识 教学法讲练结合 讲授内容纲要、要求及时间分配 第七章微分方程 一、引言:1、微分方程的引出 2、简要介绍微分方程的发展史 10分钟 3、本章内容概括 二、进行新课: §7.1微分方程的基本概念 (一)两个引例 讲解教材例1、例2引入微分方程的概念 15分钟 (二)、微分方程的有关概念(理解) 微分方程 常微分方程、偏微分方程 10分钟 微分方程的阶: 微分方程的解:通解、初始条件、特解、初值问题 (三)应用: 例3验证:函数-Ccos+Gs血:是微分方程+k2x=0的解 10分钟 例4已知函数CoCs0是微分方程+x=0的通 解,求满足初始条件0=A,x:o=0的特解. 练习: 5分钟

讲授内容纲要、要求及时间分配(附页) S7.2可分离变量的微分方程 (2节) (一)定义:如果一个一阶微分方程能写成g0d(或写成5分 y=)()的形式,那么原方程就称为可分离变量的微分方程, (二)解法: 第一步分离变量,将方程写成g)x)的形式: 10分钟 第二步两端积分:g(y)=/xk,设积分后得G0=Fx)+C 第三步求出由Gy=FHC所确定的隐函数=x)或=y) (三)讲解例题 例1求微分方程安=2的通解。 5分钟 例2铀的衰变速度与当时未衰变的原子的含量M成正比.已知0 5分钟 时铀的含量为a,求在衰变过程中铀含量M()随时间t变化的规律. 学生练习:习题7-21、2、5 10分钟 讲解教材:例3降落伞下落问题:引导学生进行受力分析并解题。 5分钟 讲解教材:例4力学问题:分析题意,列出微分方程并求解。 练习:习题7-21(1)(2) 5分钟 三、课堂小结: 要求学生理解微分方程相关概念,掌握可分离变量的微分方程的概5分 念和解法 四、布置作业:习题7-21(3)(5)(7)2(2)(3)
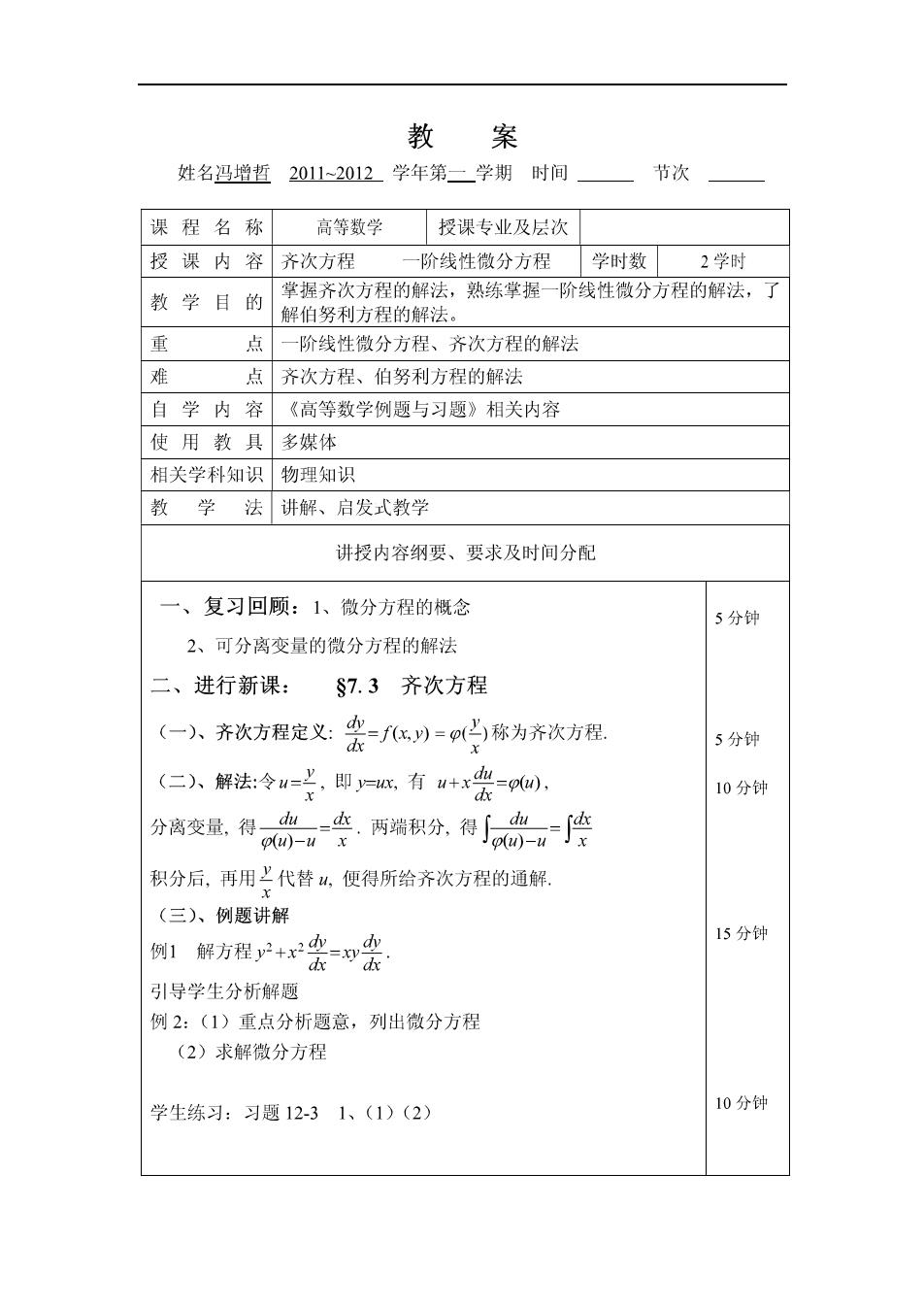
教 案 姓名冯增哲20112012学年第二学期时间 节次 课程名称 高等数学 授课专业及层次 授课内容 齐次方程 一阶线性微分方程 学时数 2学时 教学目的 草握齐次方程的解法,熟练掌握一阶线性微分方程的解法,了 解伯努利方程的解法, 一阶线性微分方程、齐次方程的解法 点齐次方程、伯努利方程的解法 自学内容《高等数学例题与习题》相关内容 使用教具多媒体 相关学科知识物理知识 教学 法讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾:1、微分方程的概念 5分钟 2、可分离变量的微分方程的解法 二、进行新课: §7.3齐次方程 (一小、齐次方程定义·密心)=的称为济次方程 5分钟 (已入、解法令卡即有+尝0。 10分钟 分离变量,得。查两积分得岛喷 积分后,再用上代替山,便得所给齐次方程的通解。 (三)、例题讲解 例1解方程户+密会 15分钟 引导学生分析解题 例2:(1)重点分析题意,列出微分方程 (2)求解微分方程 学生练习:习题12-31、(1)(2) 10分钟

讲授内容纲要、要求及时间分配(附页) S7.4一阶线性微分方程 (一人、方程密+P加-Q)叫做一阶线性微分方程 5分钟 如果Qx)0,则方程称为齐次线性方程.否则方程称为非齐次线性方程. (2节)》 (二)、常数变易公式 y=eOe达在+C(详细讲解) 10分, 创1求动程杂高-+的送款 5分钟 讲解教材例2电学问题:(1)列方程(2)解方程 10分钙 (3)对解分析 练习 5分钟 (三)、伯努利方程(简单介绍,课下自学) 5分钟 佰努利方程:安+Py=Qy-0) 解法以y除方程的两边有y一杂+P·-Q 令:一,得线性方程失+0-mPz=0-mQ). 例3求方程央名=a血8的通解 (四)、变量代换在解微分方程中的应用(简单介绍,课下自学) 5分钟 例4解方股会中 练习:习题12-41、(1)(2) 5分钟 三、课堂小结: 5分钟 1.齐次方程的概念和解法 2.一阶线性微分方程的解法 四、布置作业:习题7-31、(4)2、(1) 习题7-41、(5)(8)2、(2)(3)

教 案 姓名冯增哲 2011-2012学年二学期 时间 节次 课程名称 高等数学授课专业及层次 授课内容 可降阶的高阶微分方程 学时数2学时 教学目的 会解三种可降阶的微分方程 重 点可降阶的微分方程的解法 点第三种(不显含x)可降阶微分方程的解法 自学内容《高等数学例题与习题》相关内容 使用教具多媒体 相关学科知识物理知识 教学法讲解、启发式教学 讲授内容纲要、要求及时间分配 “、复习回顾: 1、齐次方程及其解法 2、一阶线性微分方程的解法 10分钟 二、进行新课: §7.5可降阶的高阶微分方程 (一)、y=fx)型的微分方程 解法:积分n次 5分钟 yDff(d+C. y-=jj/k+C+C,. 例1求微分方程y"”=e-cosx的通解。 5分钟 教材例2:力学应用题(1)分析题意,列出微分方程 10分创 (2)求解微分方程 练习: 5分钟 (二)、y”=xy型的微分方程(不显含) 解法:设yp则方程化为p'x,p 5分钟 设p的道解为C则来xG。 原方程的通解为y=x,Cd+C

讲授内容纲要、要求及时间分配(附页) 例3求微分方程(1+y"=2y满足初始条件k0=1,yk0=3的特解 10分钟 讲解教材例4:做分方程应用题 (1)分析题意,列出微分方程 (2)求解微分方程 学生练习习题7-51 5分钟 (三)、y"=,y型的微分方程(不显含x) 10分钟 原方程化为P来心.设方程P染0,m的适解为yp,C以 则原方超的适解为jG+G 例5求微分y”-y2-0的通解, 5分钟 讲解教材例6 10分钟 学生练习习题752、4 5分钟 三、小结:要求学生会解三种可降阶的微分方程。 四、布置作业:习题7-51、(5)(8)(10)2、(3)(10)3 5分钟

教 案 姓名冯增哲2011~2012学年第二学期时间节次 课程名称 高等数学授课专业及层次 授课内容 高阶线性微分方程 常系微齐次线性微分方程(一) 学时数2学时 教学目的 理解线性微分方程解的结构:熟练掌握特征方程法解常系数齐次线性微 分方程, 点特征方程法解常系数齐次线性微分方程 点阶常系数齐次线性微分方程的解法 自学内容《高等数学例题与习题》相关内容 使用教具多媒体 相关学科知识无 教学法讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾:可降阶的高阶微分方程的解法 二、进行新课: §7.6高阶线性微分方程 5分钟 (一)、概念 1、引例 2、二阶线性微分方程:二阶线性微分方程的一般形式为 10分钟 y"+P(r)y/+Q(rly=Ar). 若方程右端)0时,方程称为齐次的,杏则称为非齐次的 (二)、线性微分方程的解的结构 1、函数的线性相关性 5分钟 2、解的结构定理 定理1如果函数y()与)是方程y+Py+O0 5分钟 的两个解,那么y=Cy,+Cy,0也是方程的解.其中C1、C,是任意常数 引导学生分析并证明 定理2如果果函数y)与y)是方程y"+P(y+Qy=0的两个线性无关的 5分钟 解,那么=Cy+Cy)(C、C,是任意常数)足方程的通解。 定理3设v*o是二阶非齐次线性方程y+PW+Or x)的一个特解,x)是 对应的齐次方程的通解,那么)一))足阶非齐次线性微分方程的通解 5分钟 引导学生分析并证明

讲授内容纲要、要求及时间分配(附页) 定理4设非齐次线性微分方程y”+P代xy+Qxy=儿x)的右端x)儿个函数之和, 10分钟 如y"+Pxy+Q(x)y-/i(x)+A(x,而*x)与y*)分别是方程 y"+P(x)y+Q(r)v=fi(x)y+P(x)y+Q(x)y=f(r) 的特解、那么y*x)+y*x)就是原方程的特解. 引导学生分析并证明 例4验证y=cosx与2=smx是方程y”+y=0的线性无关解,并写出其通解. 5分钟 $7.7常系数齐次线性微分方程 (2节) (一)、定义:方程y"++=0称为二阶常系数齐次线性微分方程,其中p 5分钟 g均为常数 (二)、解法: 1、特征方程:方程户+pr+g=0叫做微分方程y”++=0的特征方程 2、结论:(详细讲解)》 5分钟 15分钟 (1)特征方程有两个不相等的实根1、乃时.方程的通解为 y=Cer+C:e. (2特征方程有两个相等的实根=n时,方程的通解为 y=Cew+C:xer. (3特征方程有一对共轭复根n.,二0时,方程的通解为 y=e(CicosAx+Cxsinax ) 例1求微分方程”-2y-3-0的通解。 5分钟 例2求方程y”+2y+y0满足初始条件小0=4、yx0=-2的特解 5分钟 例3求微分方程y”-2y+5=0的通解 5分钟 (三)学生练习: 5分钟 三、小结: 5分钟 1.线性微分方程的解的结构 2.常系数齐次线性微分方程的解法 布置作业:习题7-7:1、(5)(6)(10)2、(4)(6)》

教 案 姓名冯增哲2011~2012学年第二学期时间 节次 课程名称 高等数学授课专业及层次 授课内容 常系数齐次线性微分方程(二) 学时数 2学时 教学目的 然练掌特征方程法解常系数有、无阻尼齐次线性微分方程的解法 重 点特征方程法解常系数齐次线性微分方程 n阶常系数齐次线性微分方程的解法 自学内容《高等数学例题与习题》相关内容 使用教具多媒体 相关学科知识无 教学法讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾: 10分钟 1.线性微分方程的解的结构 2.常系数齐次线性微分方程的定义及解法 二、进行新课: 7.7 常系数齐次线性微分方程 (一)无阻尼情形 1,常系数无阻尼齐次线性微分方程的概念 5分钟 2.通过例题讲解常系数无阻尼齐次线性微分方程的解法 教材例4:在第六节例1中,设物体只受弹性恢复力「的作用,且在 15分钟 初瞬0时的位置为x=。,初始速度为] =。求反映物体运 动规律的函数。 小结:无阻尼自由振动的微分方程+x=0反映的振动称为 d产t 简谐振动:x=Asin(:+p) 3.简谐振动的符号及概念 5分钟

讲授内容纲要、要求及时间分配(附页) (二)有阻尼情形 例5在第六节例1中,设物体受弹性恢复力「和阻力R的作用,且 在初瞬0时的位置为x=x。,初始速度为] =。求反映物体 运动规律的函数。 解析:分三种情形: (1)小阻尼情形:nk 5分钟 结果为x=C,em-F"+C,em-Fr 振幅随时间增大时,x趋于0. 5分钟 (3)临界阻尼情形:n=k 结果为x=e"(C,+C,),随时间增大而趋于平衡. 5分钟 (三)将二阶的情形推广到n阶情形 10分钟 1.推导和结论 2.例愿解析: 例6求方程-2y"+5y”-0的通解 10分钟 例7求方程“w +0=0的通解,其中>0。 通过以上两例题让学生了解n阶线性微分方程的解法, (四)学生练习 10分钟 三、课堂小结: 5分钟 常系数有、无阻尼齐次线性微分方程的解法 四、布置作业:习题7-7:1(1)(6),2(3(4)