
第五章定积分 (Definite Integrals) 在一切理论成就中,未必再有什么象17世纪下半 叶微积分的发现那样被看作人类精神的最高胜利了。 如果在某个地方我们看到人类精神的纯粹的和唯一 的功绩,那也就是正是在这里。 恩格斯 2012329 素山医学院信息工程学院高等数学教研常

第一节 定积分的概念 (Concept of Definite Integrals) 问题的提出 二 定积分的定义 三四 定积分存在的两个充分条件 定积分的几何意义 五定积分的性质 六小结、思想方法 七思考题与判断题 2012-3-29 泰山医学院信息工程学院高等数学教研室 2

问题的提出(Introduction) 1 面积问题(Area Problem) 曲边梯形由连续曲线 y=f(x)(f(x)≥0)、 y=f(x) x轴与两条直线x=a、 A=? x=b所围成. 0 我们有两个问题要解决,一个是给出面积的定 义,一个是找出计算面积的方法。微积分的最大功 绩在于,用干净利索的方法解决了这一问题,并用 非常有效的方法解决了相当复杂的图形的面积的计 算问题。 2012.329 奉山医学院信息工程学院高等数学教研案 3
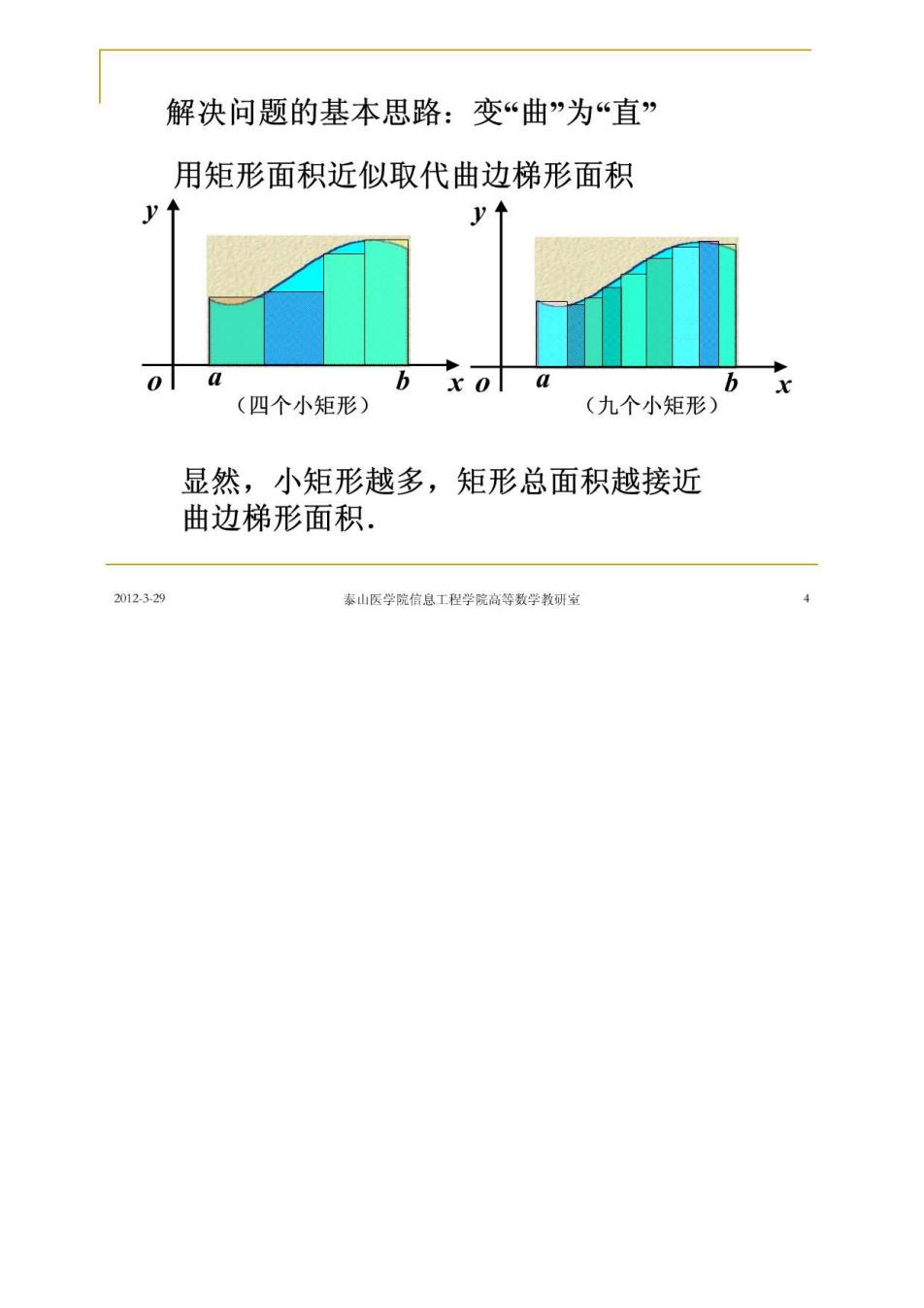
解决问题的基本思路:变“曲”为“直” 用矩形面积近似取代曲边梯形面积 xo a (四个小矩形) (九个小矩形)6 显然,小矩形越多,矩形总面积越接近 曲边梯形面积. 2012329 奉山医学院信息工程学院高等数学教研室
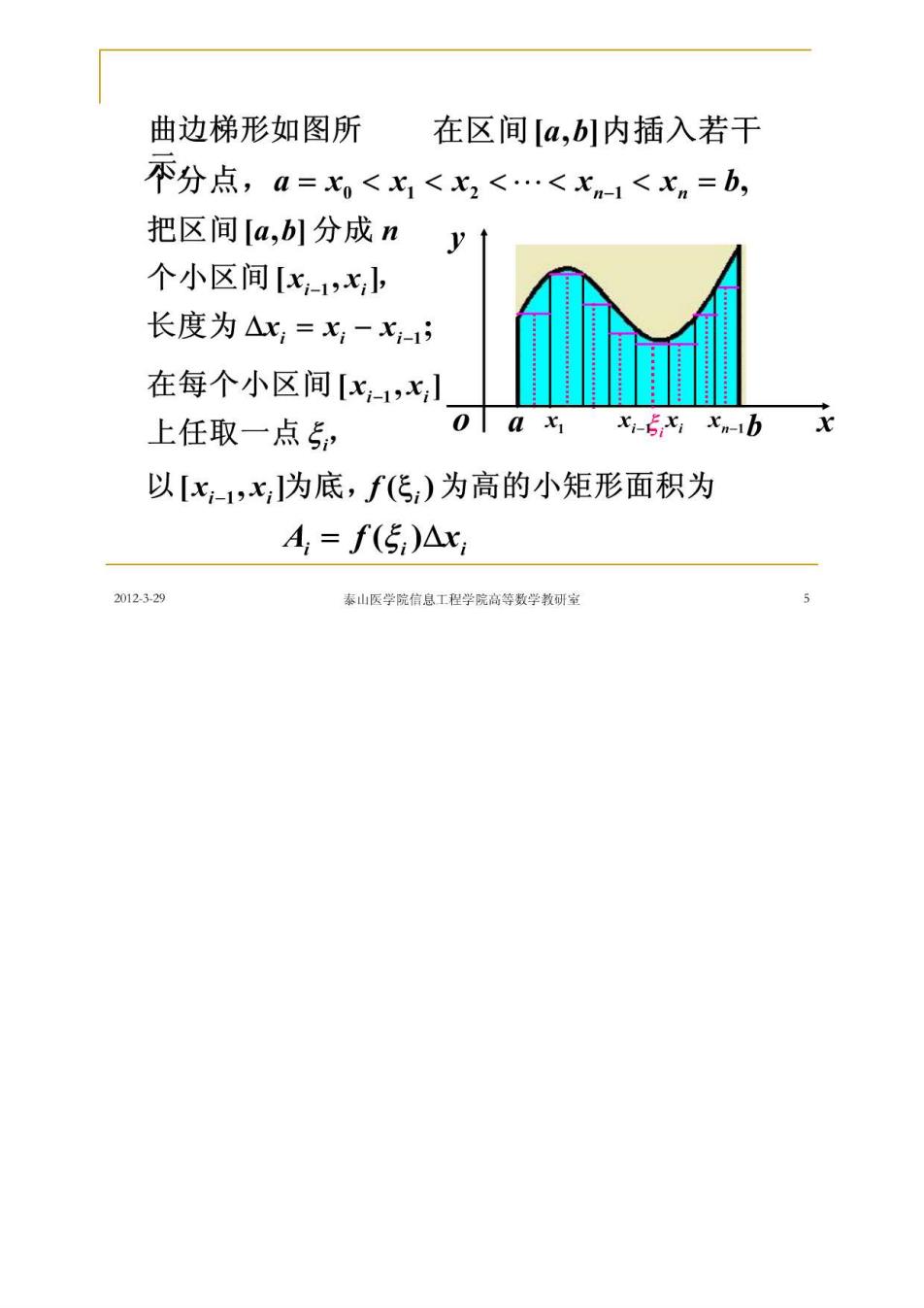
曲边梯形如图所 在区间[a,b]内插入若干 不分点,a=x<x1<x2<.<x1<xn=b, 把区间[a,b]分成n y 个小区间[x-1,x 长度为△x,=x-七- 在每个小区间[x1,x 上任取一点5, 0051x-5x,xm-1b 以[x1,x,为底,f(传)为高的小矩形面积为 A,=f(5)△x 2012329 素山医学院信息工程学院高等数学教研常

曲边梯形面积的近似值为 A≈2f5,)Ax 海 当分割无限加细,即小区间的最大长度 九=max{Ax1,△x2,.Axn} 趋近于零(九→0)时, 曲边梯形面积为A=lim∑f(5)△x, 1→0i=1 2012329 奉山医学院信息工程学院高等数学教研室

例2路程问题(Distance Problem) 设某质点作直线运动,速度v=(t)是时间 间隔T,T,】上t的一个连续函数,求物体在这 段时间内所经过的路程。 对于匀速运动,我们有公式 路程=速度X时间 解决变速运动的路程的基本思路 把整段时间分割成若干小时间段,每小段 上速度看作不变,求出各小段的路程再相加, 便得到路程的近似值,最后通过对时间的无限 细分过程求得路程的精确值, 2012329 素山医学院信息工程学院高等数学教研室

(1)分割T=t。<t1<12<.<tn-1<tn=T △t,=t:-t- (2)取点t,∈△,△s,≈v(t;)At (3)作和s≈2(c,)△M, i1 (4)取极限九=max{△t1,△t2,.,△tn} 路程的精确值s=lim∑v(x,)△t →01 2012329 奉山医学院信息工程学院高等数学教研室

定积分的定义 (Definition of Definite Integral) 定义设函数f(x)在[a,b]上有界,在a,b中任意插入 若干个分点a=X。<X<x,<.<x,<X。=b 把区间[a,b]分成n个小区间,各小区间的长度依次为 △,=x,-x-1,(i=1,2,.),在各小区间上任取 一点5,(5,∈△x,),作乘积f(5;)△x,(i=1,2,.) 并作和,S=2f传,)△x i=1 记=max{△x1,△x2,.,△xn},如果不论对[a,b] 2012329 素山医学院信息工程学院高等数学教研常
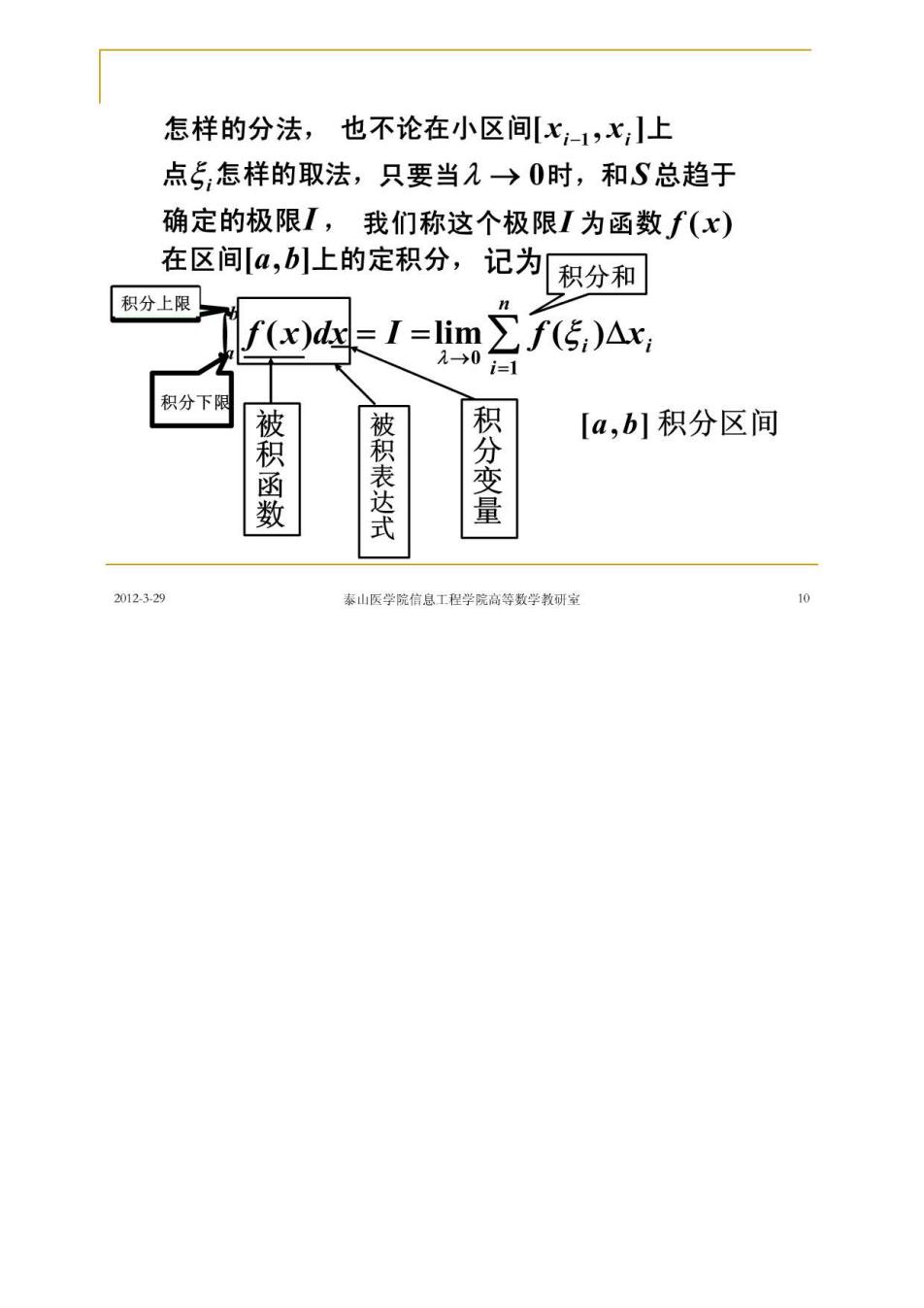
怎样的分法,也不论在小区间x1,x,上 点5怎样的取法,只要当入→0时,和S总趋于 确定的极限I,我们称这个极限I为函数f(x) 在区间[a,b]上的定积分, 记为积分和 积分上限】 fx)dI=lim2f传,)Ax, 2→01 积分下限 被积函 [a,b]积分区间 被积表达式 分变量 2012329 奉山医学院信息工程学院高等数学教研室