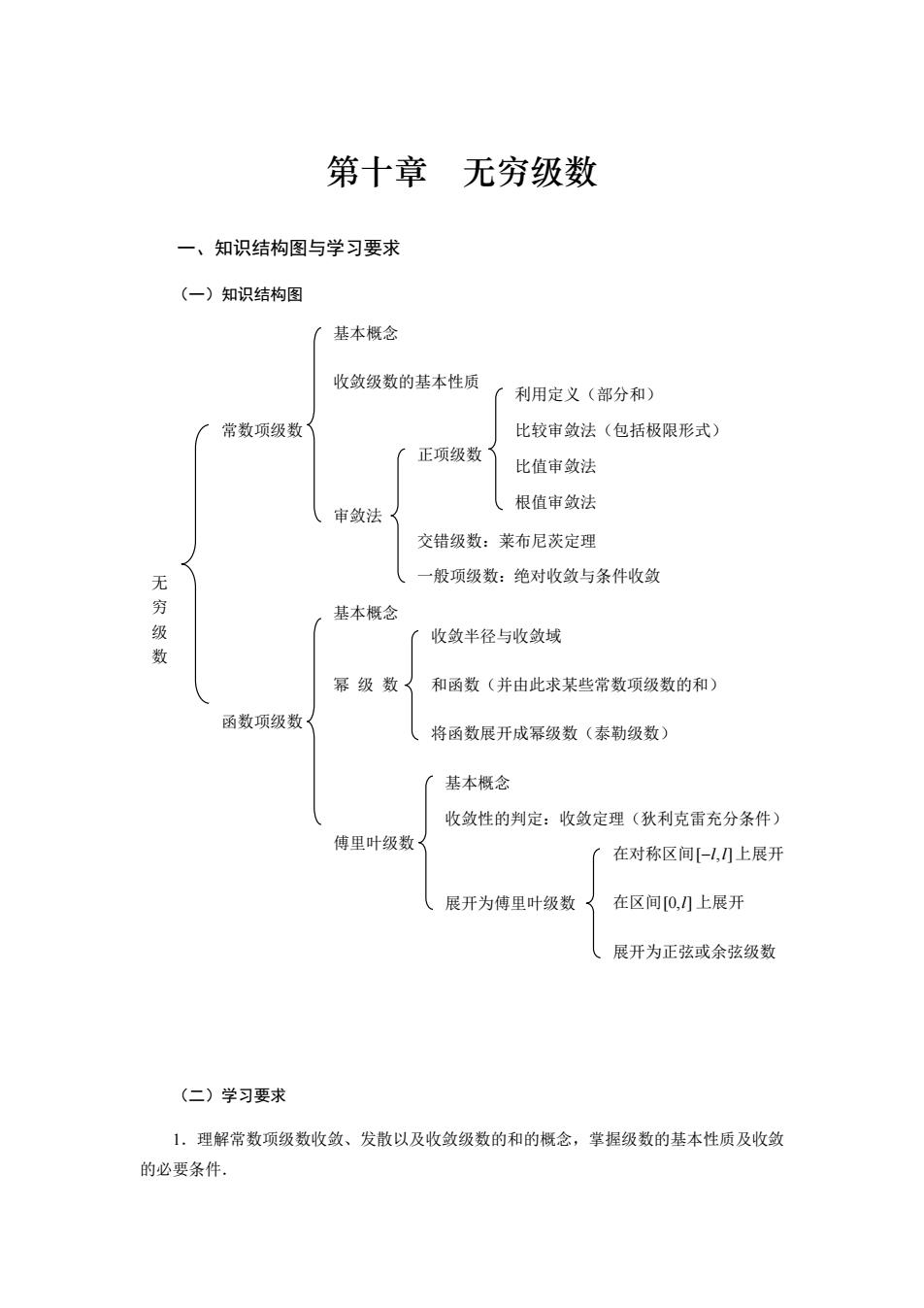
第十章 无穷级数 一、知识结构图与学习要求 (一)知识结构图 基本概念 收敛级数的基本性质 「利用定义(部分和 常数项级数 比较审敛法(包括极限形式) (正项级数 比值审敛法 审敛法 、根值审敛法 交错级数:莱布尼茨定理 无穷 一般项级数:绝对收敛与条件收敛 基本概 收敛半径与收敛域 幂级数 和函数(并由此求某些常数项级数的和) 函数项级数 ,将函数展开成幂级数(泰勒级数) 基本概念 收敛性的判定:收敛定理(狄利克雷充分条件)》 傅里叶级数 (在对称区间-1,刀上展开 展开为傅里叶级数〈在区间0,)上展开 展开为正弦或余弦级数 (二)学习要求 1,理解常数项级数收敛、发散以及收敛级数的和的概念,掌握级数的基本性质及收敛 的必要条件
第十章 无穷级数 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解常数项级数收敛、发散以及收敛级数的和的概念,掌握级数的基本性质及收敛 的必要条件. 无 穷 级 数 常数项级数 函数项级数 傅里叶级数 基本概念 审敛法 收敛级数的基本性质 一般项级数:绝对收敛与条件收敛 正项级数 比较审敛法(包括极限形式) 展开为正弦或余弦级数 比值审敛法 利用定义(部分和) 基本概念 幂 级 数 交错级数:莱布尼茨定理 根值审敛法 基本概念 收敛性的判定:收敛定理(狄利克雷充分条件) 展开为傅里叶级数 将函数展开成幂级数(泰勒级数) 和函数(并由此求某些常数项级数的和) 收敛半径与收敛域 在对称区间 [ , ] −l l 上展开 在区间 [0, ]l 上展开

2.掌握几何级数与p-级数的收敛与发散的条件。 3.掌正项级数收敛性的比较审敛法和比值市敛法,会用根值市敛法。 4.掌握交错级数的菜布尼茨审敛法。 5.了解任意项级数绝对收敛与条件收敛的概念,以及绝对收敛与条件收敛的关系。 6.了解函数项级数的收敛域及和函数的概念. 7.理解幂级数的收敛半径的概念、掌握幂级数的收敛半径、收敛区间及收敛域的求 法 8.了解幂级数在其收敛区间内的一些基本性质(和函数的连续性、逐项求导和逐项 积分),会求一些幂级数在收敛区间内的和函数,并会由此求出某些常数项级数的和. 9.了解函数展开为泰勒级数的充分必要条件. 10.掌握e、sinx、cosx、nl+x)和(1+x的麦克劳林展开式,会用它们将一些简 单函数间接展开成幂级数 11.了解傅里叶级数的概念和狄利克雷收敛定理,会将定义在[-1,】上的函数展开为傅 里叶级数,会将定义在[0,】上的函数展开为正弦级数与余弦级数,会写出傅里叶级数的和 的表达式 二、内容提要 (一)常数项级数 1.概念 ()若级数立,的部分和数列=4+%++)有极限s,即m5=5,则称 无穷级数∑山,收敛,并称s为它的和,记为5=∑4:否则称它是发散的。 (2)称级数∑u,(似,≥0,n=12)为正项级数.称级数∑(-)一u,或∑(-°4,(其中 4。>0)为交错级数 (3)如果级数立以,收敛,则称级数∑“,绝对收敛:如果级数立山,发散,而级数三 收敛,则称级数∑”,条件收敛 2.定理(性质) (1)几何级数 g=1+g+g++g+
2.掌握几何级数与 p − 级数的收敛与发散的条件. 3.掌握正项级数收敛性的比较审敛法和比值审敛法,会用根值审敛法. 4.掌握交错级数的莱布尼茨审敛法. 5.了解任意项级数绝对收敛与条件收敛的概念,以及绝对收敛与条件收敛的关系. 6.了解函数项级数的收敛域及和函数的概念. 7.理解幂级数的收敛半径的概念、掌握幂级数的收敛半径、收敛区间及收敛域的求 法. 8.了解幂级数在其收敛区间内的一些基本性质(和函数的连续性、逐项求导和逐项 积分),会求一些幂级数在收敛区间内的和函数,并会由此求出某些常数项级数的和. 9.了解函数展开为泰勒级数的充分必要条件. 10.掌握 x e 、sin x 、 cos x 、 ln(1 ) + x 和 (1 )x + 的麦克劳林展开式,会用它们将一些简 单函数间接展开成幂级数. 11.了解傅里叶级数的概念和狄利克雷收敛定理,会将定义在 [ , ] −l l 上的函数展开为傅 里叶级数,会将定义在 [0, ]l 上的函数展开为正弦级数与余弦级数,会写出傅里叶级数的和 的表达式. 二、内容提要 (一)常数项级数 1.概念 (1)若级数 1 n n u = 的部分和数列 1 2 ( ) n n n s s u u u = + + + 有极限 s ,即 lim n n s s → = ,则称 无穷级数 1 n n u = 收敛,并称 s 为它的和,记为 1 n n s u = = ;否则称它是发散的. (2)称级数 1 ( 0, 1,2, ) n n n u u n = = 为正项级数.称级数 1 1 ( 1)n n n u − = − 或 1 ( 1)n n n u = − (其中 0 n u )为交错级数. (3)如果级数 1 n n u = 收敛,则称级数 1 n n u = 绝对收敛;如果级数 1 n n u = 发散,而级数 1 n n u = 收敛,则称级数 1 n n u = 条件收敛. 2.定理(性质) (1)几何级数 2 0 1 n n n q q q q = = + + + + +

当1时收敛:而当p≤1时发散.特别地,当p=1时,调和级数 =1+分++.++. 发散 3)设级数三,和立,都收敛,则级数立以,士,)收敛,由此可知 a.若∑“,收敛,∑发散,则∑,±,)发散: b.若立.发散,工,发散,则正化,±)收敛性不定: 。若立4,与,均绝对收敛,则u,士)绝对收敛: d.若∑”绝对收敛,∑.条件收敛,则∑(以,±,)条件收敛. (4)设级数∑4.收敛,k为一个常数,则 a.∑k,收敛且im私.=0.(若m,≠0,则级数∑4,发散.) b.对∑,中的项任意加括号后所得的新级数仍收敛。(如果对级数∑,的项加括号后 所得新级数发散,则原级数发散.) (5)在级数中去掉、加上或改变有限项,不会改变级数的收敛性。 (6)如果级数∑“,绝对收敛,则级数∑4,必定收敛. 3.方法 (1)正项级数的审敛法: a.利用级数收敛的定义: b.利用级数收敛的充要条件:级数收敛一部分和数列有界: c.比较审敛法: d.比值审敛法: e.根值审敛法: £.极限审敛法。 (2)交错级数的市敛法:莱布尼茨定理. (3)一般项级数∑“,的审敛法:先转换为判别是否是收敛,若收敛,则原级数
当 q 1 时收敛,其和为 1 1− q ,而当 q 1 时发散. (2) p − 级数 1 1 1 1 1 1 2 3 p p p p n n n = = + + + + + ( p 是常数), 当 p 1 时收敛;而当 p 1 时发散.特别地,当 p =1 时,调和级数 1 1 1 1 1 1 n n n 2 3 = = + + + + + 发散. (3)设级数 1 n n u = 和 1 n n v = 都收敛,则级数 1 ( ) n n n u v = 收敛.由此可知: a.若 1 n n u = 收敛, 1 n n v = 发散,则 1 ( ) n n n u v = 发散; b.若 1 n n u = 发散, 1 n n v = 发散,则 1 ( ) n n n u v = 收敛性不定; c.若 1 n n u = 与 1 n n v = 均绝对收敛,则 1 ( ) n n n u v = 绝对收敛; d.若 1 n n u = 绝对收敛, 1 n n v = 条件收敛,则 1 ( ) n n n u v = 条件收敛. (4)设级数 1 n n u = 收敛, k 为一个常数,则 a. 1 n n ku = 收敛且 lim 0 n n u → = .(若 lim 0 n n u → ,则级数 1 n n u = 发散.) b.对 1 n n u = 中的项任意加括号后所得的新级数仍收敛.(如果对级数 1 n n u = 的项加括号后 所得新级数发散,则原级数发散.) (5)在级数中去掉、加上或改变有限项,不会改变级数的收敛性. (6)如果级数 1 n n u = 绝对收敛,则级数 1 n n u = 必定收敛. 3.方法 (1)正项级数的审敛法: a.利用级数收敛的定义; b.利用级数收敛的充要条件:级数收敛 部分和数列有界; c.比较审敛法; d.比值审敛法; e.根值审敛法; f.极限审敛法. (2)交错级数的审敛法:莱布尼茨定理. (3)一般项级数 1 n n u = 的审敛法:先转换为判别 1 n n u = 是否是收敛,若收敛,则原级数

绝对收敛,然后判别是条件收敛还是发散。 (二)函数项级数(主要讨论幂级数) 1.概念 (1)由定义在区间1上的函数列{u.(x所构成的表达式: 4(x)+,(x)+.+,(x)+. 称为定义在区间1的函数项级数,记为∑”,(x) (2)对于某个∈1,如果∑4,(G)收敛,则称是函数项级数∑“,(国的收敛点, 收敛点的全体称为∑“,)的收敛域:如果工“(化)发散,则称x是函数项级数立()的 发散点,发散点的全体称为三,()的发散域 (3)在收敛域/上,函数项级数∑“,(x)的和是x的函数,记为s(x),称sx)为函数项 级数∑4,(x)的和函数,即有 s)=∑4(x)=4(x)+4(x)+.+,(x)+,xe1. (4)5()=4(x)+,(x)++.()称为函数项级数∑,x)的部分和,则在收敛域上 有ms,()=s,称)=)-)为函数项级数()的余项 (5)形如 三ar=ata+af++ar+ 的函数项级数称为x的幂级数,而形如 2a,x-广=a+ax-+a-++a-6+. 的幂级数称为(x-)的幂级数,其中a(n=0,l2,)称为幂级数的系数。 (6)如果幂级数,”不是仅在x=0一点收敛,也不是在整个实数轴上都收敛,则 必有唯一确定的正数R存在,使得当R时,幂 级数Q,r发散,当x=R与x=-R时,幂级数,r可能收敛也可能发散.此时称正数R 为幂级数∑a,x的收敛半径.如果幂级数∑a仅在x=0处收敛,则它的收敛半径R=0:
绝对收敛,然后判别是条件收敛还是发散. (二)函数项级数(主要讨论幂级数) 1.概念 (1)由定义在区间 I 上的函数列 u x n ( ) 所构成的表达式: 1 2 ( ) ( ) ( ) n u x u x u x + + + + 称为定义在区间 I 的函数项级数,记为 1 ( ) n n u x = . (2)对于某个 0 x I ,如果 0 1 ( ) n n u x = 收敛,则称 0 x 是函数项级数 1 ( ) n n u x = 的收敛点, 收敛点的全体称为 1 ( ) n n u x = 的收敛域;如果 0 1 ( ) n n u x = 发散,则称 0 x 是函数项级数 1 ( ) n n u x = 的 发散点,发散点的全体称为 1 ( ) n n u x = 的发散域. (3)在收敛域 I 上,函数项级数 1 ( ) n n u x = 的和是 x 的函数,记为 sx( ) ,称 sx( ) 为函数项 级数 1 ( ) n n u x = 的和函数,即有 sx( ) = 1 ( ) n n u x = = 1 2 ( ) ( ) ( ) n u x u x u x + + + + , x I . (4) 1 2 ( ) ( ) ( ) ) ( n n s x = u x u x u + + + x 称为函数项级数 1 ( ) n n u x = 的部分和,则在收敛域上 有 lim ( ) ( ) n n s x s x → = ,称 ( ) ( ) ( ) n n r x s x s x = − 为函数项级数 1 ( ) n n u x = 的余项. (5)形如 2 0 1 2 0 n n n n n a x a a x a x a x = = + + + + + 的函数项级数称为 x 的幂级数,而形如 2 0 0 1 0 2 0 0 0 ( ) ( ) ( ) ( ) n n n n n a x x a a x x a x x a x x = − = + − + − + + − + 的幂级数称为 0 ( ) x x − 的幂级数,其中 ( 0,1,2, ) n a n = 称为幂级数的系数. (`6)如果幂级数 0 n n n a x = 不是仅在 x = 0 一点收敛,也不是在整个实数轴上都收敛,则 必有唯一确定的正数 R 存在,使得当 x R 时,幂级数 0 n n n a x = 绝对收敛,当 x R 时,幂 级数 0 n n n a x = 发散,当 x R = 与 x R =− 时,幂级数 0 n n n a x = 可能收敛也可能发散.此时称正数 R 为幂级数 0 n n n a x = 的收敛半径.如果幂级数 0 n n n a x = 仅在 x = 0 处收敛,则它的收敛半径 R = 0;

如果幕级数∑a,在整个实数轴上收敛,则它的收敛半径R=+0。 开区间(一R风)称为幂级数∑a,”的收敛区间,而幂级数∑a,r的收敛域是(一R,R) (R风,【R)及-R风其中之一 (7)如果函数f(x)在点,的某邻域内具有各阶导数f(x),(x),(x),则 (x-)的幂级数 n-xr一2g-r 称为函数∫x)的泰物级数.特别取x,=0,则级数变为 称此级数为麦克劳林级数 2.定理(性质) (1)AbeI定理 如果幂级数∑a,x当x=x(≠0)时收敛,则适合不等式的一切x使这 幂级数发散。 @)设级故字0,知果回p,其中a、是蒂级数空a的相每两顶 的系数,则该幂级数的收敛半径 1 R= D P*0 +,p=0 0,p= 注定理中条件回侣仅仅是求幂级数收敛半径的充分条件,而非必要条件。 (3)幂级数∑a,x的和函数s)在其收敛域1上连续 (4)幂级数工4,的和函数s()在其收敛域/上可积,并有逐项积分公式 st-吃a,r-2a,r=2+r,xeD
如果幂级数 0 n n n a x = 在整个实数轴上收敛,则它的收敛半径 R = + . 开区间 ( , ) −R R 称为幂级数 0 n n n a x = 的收敛区间,而幂级数 0 n n n a x = 的收敛域是 ( , ) −R R , ( , ] −R R ,[ , ) −R R 及 [ , ] −R R 其中之一. (7)如果函数 f x( ) 在点 0 x 的某邻域内具有各阶导数 ( ) ( ), ( ), , ( ), n f x f x f x ,则 0 ( ) x x − 的幂级数 ( ) 0 0 2 0 0 0 0 0 ( ) ( ) ( ) ( )( ) ( ) ( ) 2! ! n n f x f x f x f x x x x x x x n + − + − + + − + = ( ) 0 0 0 ( ) ( ) ! n n n f x x x n = − 称为函数 f x( ) 的泰勒级数.特别取 0 x = 0,则级数变为 ( ) ( ) 2 0 (0) (0) (0) (0) (0) 2! ! ! n n n n n f f f f f x x x x n n = + + + + + = , 称此级数为麦克劳林级数. 2.定理(性质) (1) Abel 定理 如果幂级数 0 n n n a x = 当 0 0 x x x = ( 0) 时收敛,则适合不等式 0 x x 的一切 x 使这幂级数 绝对收敛;反之,如果幂级数 0 n n n a x = 当 0 x x = 时发散,则适合不等式 0 x x 的一切 x 使这 幂级数发散. (2)设幂级数 0 n n n a x = ,如果 1 lim n n n a a + → = ,其中 n a 、 n 1 a + 是幂级数 0 n n n a x = 的相邻两项 的系数,则该幂级数的收敛半径 1 , 0 , 0 0 , R = + = = + . 注 定理中条件 1 lim n n n a a + → = 仅仅是求幂级数收敛半径的充分条件,而非必要条件. (3)幂级数 0 n n n a x = 的和函数 sx( ) 在其收敛域 I 上连续. (4)幂级数 0 n n n a x = 的和函数 sx( ) 在其收敛域 I 上可积,并有逐项积分公式 0 ( ) x s x dx = 0 [ ] x n n o n a x dx = = 0 0 x n n n a x dx = = 1 0 1 n n n a x n + = + ,( ) x I .

逐项积分后所得到的幂级数与原级数有相同的收敛半径. (5)幕级数∑a,”的和函数s(x)在其收敛区间(-R)内可导,并有逐项求导公式 sx)=(∑axy=ary=∑m,x,< 逐项求导后所得到的幂级数与原级数有相同的收敛半径. (6)设函数fx)在点x,的某一邻域U:,)内具有各阶导数,则fx)在该邻域内 能民开成春饭数空。一了的充分必要条件是©的春号公式中的余项 R国-x- (n+10 (5是介于x与x,之间的某个值)当n→o时的极限为零,即 IimR(x)=0(x∈U()). (7)如果函数)在点的某一邻域U()内能展开成泰勒级数a.-x广,则a, 是唯一的,即a=a=0.L2 nl 3.方法 (1)幂级数的收敛性判定 8.形如工a,r幂级数,利用阿贝尔定理。 b.对于幂级数∑a,(x-x”,只要令x-x=1,就可以转化为幂级数∑a,再利用 阿贝尔定理求解 c.对于一般函数项级数∑“.()的收敛性判定,通常是把x看成常数,先讨论∑,(x 的收敛性,得到一收敛区间,再讨论该区间端点处的收敛性 (2)幂级数的收敛半径的求法 半径 R= 0,p=0 0 p=+切
逐项积分后所得到的幂级数与原级数有相同的收敛半径. (5)幂级数 0 n n n a x = 的和函数 sx( ) 在其收敛区间 ( , ) −R R 内可导,并有逐项求导公式 1 0 0 1 ( ) ( ) ( ) n n n n n n n n n s x a x a x na x − = = = = = = ,( ) x R . 逐项求导后所得到的幂级数与原级数有相同的收敛半径. (6) 设函数 f x( ) 在点 0 x 的某一邻域 0 U x( ) 内具有各阶导数,则 f x( ) 在该邻域内 能展开成泰勒级数 ( ) 0 0 0 ( ) ( ) ! n n n f x x x n = − 的充分必要条件是 f x( ) 的泰勒公式中的余项 ( 1) 1 0 ( ) ( ) ( ) ( 1)! n n n f R x x x n + + = − + ( 是介于 x 与 0 x 之间的某个值)当 n → 时的极限为零,即 0 lim ( ) 0 ( ( ) ) n n R x x U x → = . (7) 如果函数 f x( ) 在点 0 x 的某一邻域 0 U x( ) 内能展开成泰勒级数 0 0 ( )n n n a x x = − ,则 n a 是唯一的,即 ( ) 0 ( ) ( 0,1,2, ) ! n n f x a n n = = . 3.方法 (1)幂级数的收敛性判定 a.形如 0 n n n a x = 幂级数,利用阿贝尔定理. b.对于幂级数 0 0 ( )n n n a x x = − ,只要令 0 x x t − = ,就可以转化为幂级数 0 n n n a t = ,再利用 阿贝尔定理求解. c.对于一般函数项级数 1 ( ) n n u x = 的收敛性判定,通常是把 x 看成常数,先讨论 1 ( ) n n u x = 的收敛性,得到一收敛区间,再讨论该区间端点处的收敛性. (2)幂级数的收敛半径的求法 a.对于 0 ( 0,1,2, ) n a n = 的幂级数 0 n n n a x = ,由 1 lim n n n a a + → = 或 lim n n n a → = ,得收敛 半径 1 , 0 , 0 0 , R = + = = + .

b.对于缺项的幂级数∑4(x),不能用上述公式,而应直接使用函数项级数的比值法 求超限回,或使用限值法求极限四同=小.当1时,幂级数发散,从而根据幂级数收敛半径的定义求得收敛半径R, (3)幂级数的收敛域的求法 求出幂级数的收敛半径R后,再对x=±R时所得常数项级数判定其收敛性,最终求出 收敛域,即区间(←RR),(←R,一RR)和-R网其中之一 (4)幂级数在收敛域内的和函数 a,熟知的一些常用级数的和函数: =-t+lren+-2r产wco 1 1 1 1 osx=l-+r-+l旷2+-2-lヅ2m产(<x<+m -0 功-号+号4r行一空-r行0 n! b.其次要善于利用适当的变量代换、幂级数的代数运算和幂级数在其收敛域内进行的 逐项求导、积分运算,把所讨论级数化成其和函数是己知的幂级数的形式,并求其和: c.然后对应步骤b中所作运算再作相应的逆运算,即可求得原幂级数的和函数: .但要注意,上述运算均应在幂级数的收敛区间内进行,故和函数的后面,必须注明 收敛区间.因此,在求和函数之前要先求收敛域。 (5)利用幂级数求某些常数项级数的和 根据该常数项级数的特点,构造出一个幂级数或几个幂级数的和,使其在收敛域中某 点x的值恰好是这个常数项级数,然后再按照求幂级数和函数的方法求出幂级数的和函数, 最后求出该和函数在,处的值,即得所求常数项级数的和 (6)幂级数的运算 。两个收敛的幂级数相加、相减或相乘,所得幂级数的收敛区间取原来两个幂级数的 收敛区间的公共部分,而相除所得的幂级数的收敛区间则比原来两个幂级数的收敛区间小。 b.对幂级数逐项求导或逐项积分所得的幂级数与原来幂级数有相同的收敛半径R,但 在点x=±R处,幂级数的敛散性可能发生变化,必须重新讨论. (7)函数展开成x的幂级数
b.对于缺项的幂级数 1 ( ) n n u x = ,不能用上述公式,而应直接使用函数项级数的比值法 求极限 1 ( ) lim ( ) ( ) n n n u x x u x + → = ,或使用根值法求极限 lim ( ) ( ) n n n u x x → = .当 ( ) 1 x 时,幂级数 收敛;当 ( ) 1 x 时,幂级数发散,从而根据幂级数收敛半径的定义求得收敛半径 R . (3)幂级数的收敛域的求法 求出幂级数的收敛半径 R 后,再对 x R = 时所得常数项级数判定其收敛性,最终求出 收敛域,即区间 ( , ) −R R , ( , ] −R R ,[ , ) −R R 和 [ , ] −R R 其中之一. (4)幂级数在收敛域内的和函数 a.熟知的一些常用级数的和函数: 2 0 1 1 1 1 2! ! ! x n n n e x x x x n n = = + + + + + = ( ), − + x 1 1 3 1 2 1 sin ( 1) 3! (2 1)! n n x x x x n − − = − + + − + − 1 1 1 1 2 ( 1) ( ) (2 , 1)! n n n x x n = − − = − − + − 1 1 1 2 4 2 cos 1 ( 1) 2! 4! (2 )! n n x x x x n = − + − + − + 0 1 2 ( 1) (2 )! n n n x n = = − ( ), − + x 2 0 1 1 1 1 1 n n n x x x x x x = = + + + + + = − (- ), 2 3 1 1 0 ln(1 ) ( 1) ( 1) ( 1 1), 2 3 1 1 n n n n n x x x x x x x n n + + = + = − + − + − + = − − + + 2 ( 1) ( 1).( 1) (1 ) 1 1 1 2! ! m n m m m m m n x mx x x x n − − − + + = + + + + + (- ). b.其次要善于利用适当的变量代换、幂级数的代数运算和幂级数在其收敛域内进行的 逐项求导、积分运算,把所讨论级数化成其和函数是已知的幂级数的形式,并求其和; c.然后对应步骤 b 中所作运算再作相应的逆运算,即可求得原幂级数的和函数; d.但要注意,上述运算均应在幂级数的收敛区间内进行,故和函数的后面,必须注明 收敛区间.因此,在求和函数之前要先求收敛域. (5)利用幂级数求某些常数项级数的和 根据该常数项级数的特点,构造出一个幂级数或几个幂级数的和,使其在收敛域中某一 点 0 x 的值恰好是这个常数项级数,然后再按照求幂级数和函数的方法求出幂级数的和函数, 最后求出该和函数在 0 x 处的值,即得所求常数项级数的和. (6)幂级数的运算 a.两个收敛的幂级数相加、相减或相乘,所得幂级数的收敛区间取原来两个幂级数的 收敛区间的公共部分,而相除所得的幂级数的收敛区间则比原来两个幂级数的收敛区间小. b.对幂级数逐项求导或逐项积分所得的幂级数与原来幂级数有相同的收敛半径 R ,但 在点 x R = 处,幂级数的敛散性可能发生变化,必须重新讨论. (7)函数展开成 x 的幂级数

a.直接法可分如下四步进行: 第一步:求出函数fx)的各阶导数fx),了(x,(x),如果在x=0处某阶导数 不存在,就停止进行. 第二步:求出函数f(x)的各阶导数f(x,fx,.,(x,.在x=0处的值: f(0).f(0).f"(0).·,f(0. 第三步:写出幂级数 j0+f0x+0x++0r+.或20r 2 n! 并求出收敛半径R. 第四步:考察当x在区间(RR)内时的余项 R=包 (n+1)1 的极限 ▣=如得,(5在0与之同 是否为零.如果为零,则函数fx)在区间(~R,)内的幂级数展开式为 =0+0r+9++0r+-2%0r. 其中-R<x<R. b.间接法 将所给函数拆成部分和的形式或者通过求导数、求积分将其化成其幂级数展开式为已知 的函数(如心,5血xos己+)及0+等),然后再利用这些函数的幂级数展开式 进行逐项求导或逐项积分来达到将所给函数展开成幂级数的目的,这样微不但计算简单,而 且可以避免研究余项。但要注意,这种展开运算也是在幂级数的收敛区间内进行的,因此, 最后必须注明幂级数的收敛域, (三)傅里叶级数 1.概念 (1)形如 受+a,eosm+hmm) 的级数叫做三角级数 (2)三角函数系 {1,cosx.sinx,··,C0sx,sinr,·】 中任何不同的两个函数的乘积在区间一,]上的积分等于零,即
a.直接法 可分如下四步进行: 第一步:求出函数 f x( ) 的各阶导数 ( ) ( ), ( ), , ( ), n f x f x f x ,如果在 x = 0 处某阶导数 不存在,就停止进行. 第二步:求出函数 f x( ) 的各阶导数 ( ) ( ), ( ), , ( ), n f x f x f x 在 x = 0 处的值: ( ) (0), (0), (0), , (0), n f f f f 第三步:写出幂级数 ( ) 2 (0) (0) (0) (0) 2! ! n n f f f f x x x n + + + + + 或 ( ) 0 (0) ! n n n f x n = , 并求出收敛半径 R . 第四步:考察当 x 在区间 ( , ) −R R 内时的余项 ( 1) 1 ( ) ( ) ( 1)! n n n f R x x n + + = + 的极限 ( 1) 1 ( ) lim ( ) lim , ( 1)! n n n n n f R x x n + + → → = + ( 在 0 与 x 之间) 是否为零.如果为零,则函数 f x( ) 在区间 ( , ) −R R 内的幂级数展开式为 ( ) 2 (0) (0) ( ) (0) (0) 2! ! n n f f f x f f x x x n = + + + + + = ( ) 0 (0) ! n n n f x n = , 其中 − R x R. b.间接法 将所给函数拆成部分和的形式或者通过求导数、求积分将其化成其幂级数展开式为已知 的函数(如 1 ,sin ,cos , ,ln(1 ) 1 x e x x x x + − 及 (1 )m + x 等),然后再利用这些函数的幂级数展开式 进行逐项求导或逐项积分来达到将所给函数展开成幂级数的目的.这样做不但计算简单,而 且可以避免研究余项.但要注意,这种展开运算也是在幂级数的收敛区间内进行的,因此, 最后必须注明幂级数的收敛域. (三)傅里叶级数 1.概念 (1)形如 0 1 ( cos sin ) 2 n n n a a nx b nx = + + 的级数叫做三角级数. (2)三角函数系 { 1,cos ,sin , ,cos ,sin , x x nx nx } 中任何不同的两个函数的乘积在区间 [ , ] − 上的积分等于零,即

[cosn=0(n=12.3.). [sinnx dx=0 (n=1.2.3.), sin k cos在=0k,n=l2,3 =0传n=l23k≠川, sin kx sinvx本=0(k,n=l2,3.,k≠m 称此三角函数系在区间[元,]上正交 (3)设函数fx)在区间[-元,上可积,则 .(coe(in( 称为函数fx)的傅里叶系数, (4)由函数∫x)的傅里叶系数所构成的三角级数 称为函数∫x)的傅里叶级数,记为 f闭-2+2as+久snm. (5)设函数f)在区间一元,]上可积。当fx)为奇函数时,fx)的傅里叶系数为 a=0(a=0L2小,6=2f)sinm本a=l2小 f)的傅里叶级数为∑6,sinr,此时称其为正弦级数:当fx)为偶函数时,fx)的傅里 叶系数为 ()d(.(). )的傅里叶级数为受+a,c0s心,此时称其为余弦级数。 (6)设函数(x)定义在区间0,]上并且满足收敛定理的条件,在开区间(一π,0)内补 充函数fx)的定义,得到定义在(←元,上的函数F(x),使它在(←元,)上成为奇函数(偶函 数).。按这种方式拓广函数定义域的过程称为奇延拓(偶延拓) 2.定理(性质) (1)收敛定理(狄利克雷(Dirichlet)充分条件) 设f)是周期为2π的周期函数,如果它满足:在一个周期内连续或只有有限个第一类 间断点,且在一个周期内至多只有有限个极值点,则x)的傅里叶级数收敛,并且其和函 数
cos 0 ( 1,2,3, ) nx dx n − = = , sin 0 ( 1,2,3, ) nx dx n − = = , sin cos 0 ( , 1,2,3, ) kx nx dx k n − = = , cos cos 0 ( , 1,2,3, , ) kx nx dx k n k n − = = , sin sin 0 ( , 1,2,3, , ) kx nx dx k n k n − = = . 称此三角函数系在区间 [ , ] − 上正交. (3)设函数 f x( ) 在区间 [ , ] − 上可积,则 1 ( )cos ( 0,1, ) n a f x nx dx n − = = , 1 ( )sin ( 1,2, ) n b f x nx dx n − = = , 称为函数 f x( ) 的傅里叶系数. (4)由函数 f x( ) 的傅里叶系数所构成的三角级数 0 1 ( cos sin ) 2 n n n a a nx b nx = + + 称为函数 f x( ) 的傅里叶级数,记为 0 1 ( ) ( cos sin ) 2 n n n a f x a nx b nx = + + . (5)设函数 f x( ) 在区间 [ , ] − 上可积.当 f x( ) 为奇函数时, f x( ) 的傅里叶系数为 0 ( 0,1,2, ) n a n = = , 0 2 ( )sin ( 1,2, ) n b f x nx dx n = = , f x( ) 的傅里叶级数为 1 sin n n b nx = ,此时称其为正弦级数;当 f x( ) 为偶函数时, f x( ) 的傅里 叶系数为 0 2 ( )cos ( 0,1,2, ) n a f x nx dx n = = , 0 ( 1,2, ) n b n = = , f x( ) 的傅里叶级数为 0 1 cos 2 n n a a nx = + ,此时称其为余弦级数. (6)设函数 f x( ) 定义在区间 [0, ] 上并且满足收敛定理的条件,在开区间 ( ,0) − 内补 充函数 f x( ) 的定义,得到定义在 ( , ] − 上的函数 F x( ) ,使它在 ( , ) − 上成为奇函数(偶函 数).按这种方式拓广函数定义域的过程称为奇延拓(偶延拓). 2.定理(性质) (1)收敛定理(狄利克雷(Dirichlet)充分条件) 设 f x( ) 是周期为 2 的周期函数,如果它满足:在一个周期内连续或只有有限个第一类 间断点,且在一个周期内至多只有有限个极值点,则 f x( ) 的傅里叶级数收敛,并且其和函 数

)=受+2a,cosx+6,smm) 满足: 「fx, x为/(x)的连续点 -+的间断盒 (2)设周期为21的周期函数x)满足收敛定理的条件,则它的傅里叶级数展开为 /=2+2a,cos"+6sm5,ge0. 其中 ()cos (.2). 6=/e)sim"T产n=l2.3 C=fx)=与Ux)+fxB. a.当/)为奇函数时,f)=A,si血ceC,其中 b()sin xd (n=12.3.). .当为偶函数时,)-受+2a,os”学《eO,其中 a-2/cs"km=01,2
0 1 ( ) ( cos sin ) 2 n n n a s x a nx b nx = = + + 满足: ( ), ( ) ( ) 1 [ ( ) ( )], ( ) 2 f x x f x s x f x f x x f x − + = + 为 的连续点 为 的间断点 . (2)设周期为 2l 的周期函数 f x( ) 满足收敛定理的条件,则它的傅里叶级数展开为 0 1 ( ) ( cos sin ) , ( ) 2 n n n a n x n x f x a b x C l l = = + + , 其中 1 ( )cos ( 0,1,2, ) l n l n x a f x dx n l l − = = , 1 ( )sin ( 1,2,3, ) l n l n x b f x dx n l l − = = , 1 { ( ) [ ( ) ( )] 2 C x f x f x f x } − + = = + . a. 当 f x( ) 为奇函数时, 1 ( ) sin ( ) n n n x f x b x C l = = ,其中 0 2 ( )sin ( 1,2,3, ) l n n x b f x dx n l l = = . b. 当 f x( ) 为偶函数时, 0 1 ( ) cos ( ) 2 n n a n x f x a x C l = = + ,其中 0 2 ( )cos ( 0,1,2, ) l n n x a f x dx n l l = = .