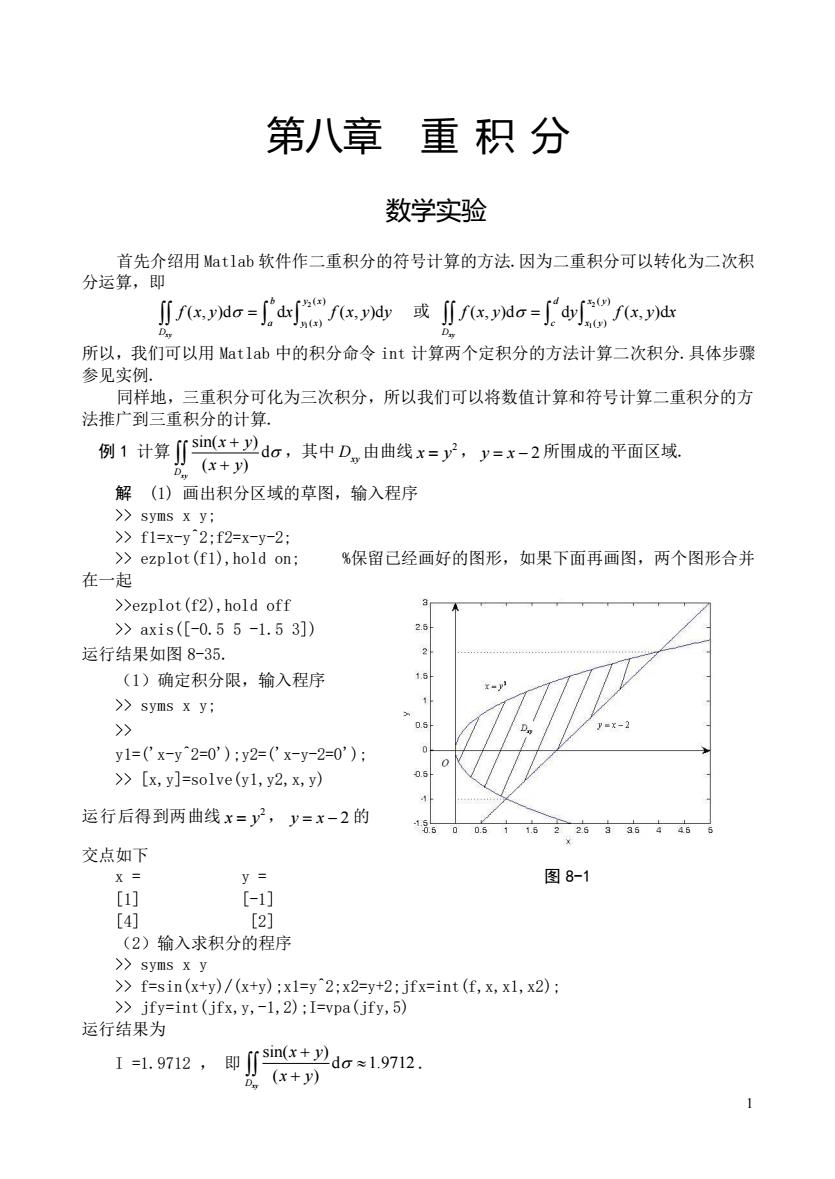
第八章 重积分 数学实验 首先介绍用Matlab软件作二重积分的符号计算的方法.因为二重积分可以转化为二次积 分运算,即 ∬f,ag=df,t或fxdo=d时fxd 所以,我们可以用Matlab中的积分命令int计算两个定积分的方法计算二次积分.具体步骤 参见实例. 同样地,三重积分可化为三次积分,所以我们可以将数值计算和符号计算二重积分的方 法推广到三重积分的计算. 例1计算∬smx+》do,其中D,由曲线x=y广,y=x-2所围成的平面区域 (x+y) 解(1)画出积分区域的草图,输入程序 >f1= :f2=x-y-2 >>ezplot (f),hold on %保留已经画好的图形,如果下面再画图,两个图形合并 在一 >>ezplot(f2),hold off >axis([-0.55-1.53] 运行结果如图8-35. (1)确定积分限,输入程序 >》syms x y: y=x-2 y1='x-y^2=0'):y2=('x-y-2=0'): >>[x,y]=solve(y1,y2,x,y) 运行后得到两曲线x=y2,y=x-2的 6226a446 交点如下 Y= y= 图8-1 [1] [-1 121 (2)输入求积分的程序 >syms x y >f=sin(xty)/(xty);x1=y"2:x2=y+2:jfx=int(f,x,x1,x2): >>jfy=int(jfx,y,-1,2):I=vpa(jfy,5) 运行结果为 I=1.9712,即∬x+2do19712. D
1 第八章 重积分 数学实验 首先介绍用 Matlab 软件作二重积分的符号计算的方法.因为二重积分可以转化为二次积 分运算,即 2 1 ( ) ( ) ( , )d d ( , )d xy b y x a y x D f x y x f x y y = 或 2 1 ( ) ( ) ( , )d d ( , )d xy d x y c x y D f x y y f x y x = 所以,我们可以用 Matlab 中的积分命令 int 计算两个定积分的方法计算二次积分.具体步骤 参见实例. 同样地,三重积分可化为三次积分,所以我们可以将数值计算和符号计算二重积分的方 法推广到三重积分的计算. 例 1 计算 sin( ) d ( ) Dxy x y x y + + ,其中 D xy 由曲线 2 x y = , y x = − 2 所围成的平面区域. 解 (1) 画出积分区域的草图,输入程序 >> syms x y; >> f1=x-y^2;f2=x-y-2; >> ezplot(f1),hold on; %保留已经画好的图形,如果下面再画图,两个图形合并 在一起 >>ezplot(f2),hold off >> axis([-0.5 5 -1.5 3]) 运行结果如图 8-35. (1)确定积分限,输入程序 >> syms x y; >> y1=('x-y^2=0');y2=('x-y-2=0'); >> [x,y]=solve(y1,y2,x,y) 运行后得到两曲线 2 x y = , y x = − 2 的 交点如下 x = y = 图 8-1 [1] [-1] [4] [2] (2)输入求积分的程序 >> syms x y >> f=sin(x+y)/(x+y);x1=y^2;x2=y+2;jfx=int(f,x,x1,x2); >> jfy=int(jfx,y,-1,2);I=vpa(jfy,5) 运行结果为 I =1.9712 , 即 sin( ) d 1.9712 ( ) Dxy x y x y + +

例2计算zddd,其中2为平面2r+3y+:=2与三个坐标面所围成的空间区域, 解相应的Matlab程序为 >》syms x y z >》f=x*y*z; >》z1=0:z2=(2-2*x-3*y): >>v1=0:v2=(2-2*x)/3: >fz=int (f,z,zl,22) >》fy=int(f,y,1,y2) >I=int(fy,x,0,1) 结果为1=1/405,即p=drdd 1 405 例3计算抛物面:=x2+y2在平面:=1下方的面积. 解(1)首先作图,相应的Matlab程序为 >>[x,y]=meshgrid(-1:0.1:1): >》z=x.2y.^2 >z1=ones(size(z):%产生一个由元素1组成的与:同维的向量 >》surf(x,y,z)%画抛物面:=x2+y2的图形 >>hold on >mesh(x,y,z1) %画平面:=1的图形 运行后显示如图8-36所示 (2)计算面积,相应的Matlab程序为 >》syms x y z r t >》2x24y2 》f=sart0+diff,x)2+diff,)2: >〉x=r*C0s(t): >y=r*sin(t); >》f1=subs(f):%将f中的x,y变量用新定义的x,y表达式替换 >>f2=int(f1*r.r.0.1): >>s=int(f2,t,0,2*pi) 结果为s-V6p45/65☒p,即所求曲面面织为s5-} 图8-2 2
2 例 2 计算 xyz x y z ddd ,其中 为平面 2 3 2 x y z + + = 与三个坐标面所围成的空间区域. 解 相应的 Matlab 程序为 >> syms x y z >> f=x*y*z; >> z1=0;z2=(2-2*x-3*y); >> y1=0;y2=(2-2*x)/3; >> fz=int(f,z,z1,z2); >> fy=int(fz,y,y1,y2); >> I=int(fy,x,0,1) 结果为 I =1/405 ,即 1 ddd 405 xyz x y z = . 例 3 计算抛物面 2 2 z x y = + 在平面 z =1 下方的面积. 解 (1)首先作图,相应的 Matlab 程序为 >> [x,y]=meshgrid(-1:0.1:1); >> z=x.^2+y.^2; >> z1=ones(size(z)); %产生一个由元素 1 组成的与 z 同维的向量 >> surf(x,y,z) %画抛物面 2 2 z x y = + 的图形 >> hold on >> mesh(x,y,z1) %画平面 z =1 的图形 运行后显示如图 8-36 所示 (2)计算面积,相应的 Matlab 程序为 >> syms x y z r t >> z=x^2+y^2; >> f=sqrt(1+diff(z,x)^2+diff(z,y)^2); >> x=r*cos(t); >> y=r*sin(t); >> f1=subs(f); %将 f 中的 x,y 变量用新定义的 x,y 表达式替换 >> f2=int(f1*r,r,0,1); >> s=int(f2,t,0,2*pi) 结果为 s =-1/6*pi+5/6*5^(1/2)*pi,即所求曲面面积为 5 5 1 6 6 S = − . 图 8-2