第八章重积分 一、知识结构图与学习要求 (一)知识结构图 概念与基本性质 二重积分 「在直角坐标系下 (计 算 在极坐标系下 概念与基本性质 三重积分〈 在直角坐标系下 计 在柱面坐标系下 在球面坐标系下 平面图形的面积 几何应用《 曲面的面积 空间立体的体积 重积分的应用 〔质心 物理应用子 转动惯量 (引力 (二)学习要求 1.理解二重积分、三重积分的概念,了解重积分的性质与二重积分的中值定理 2.掌握二重积分的计算(直角坐标、极坐标),会计算三重积分(直角坐标、柱 面坐标、球面坐标). 3.会用重积分求一些简单的几何量与物理量(平面图形的面积、曲面的面积、空间 立体的体积、质量、质心、转动惯量、引力等). 二、内容提要 (一)二重积分
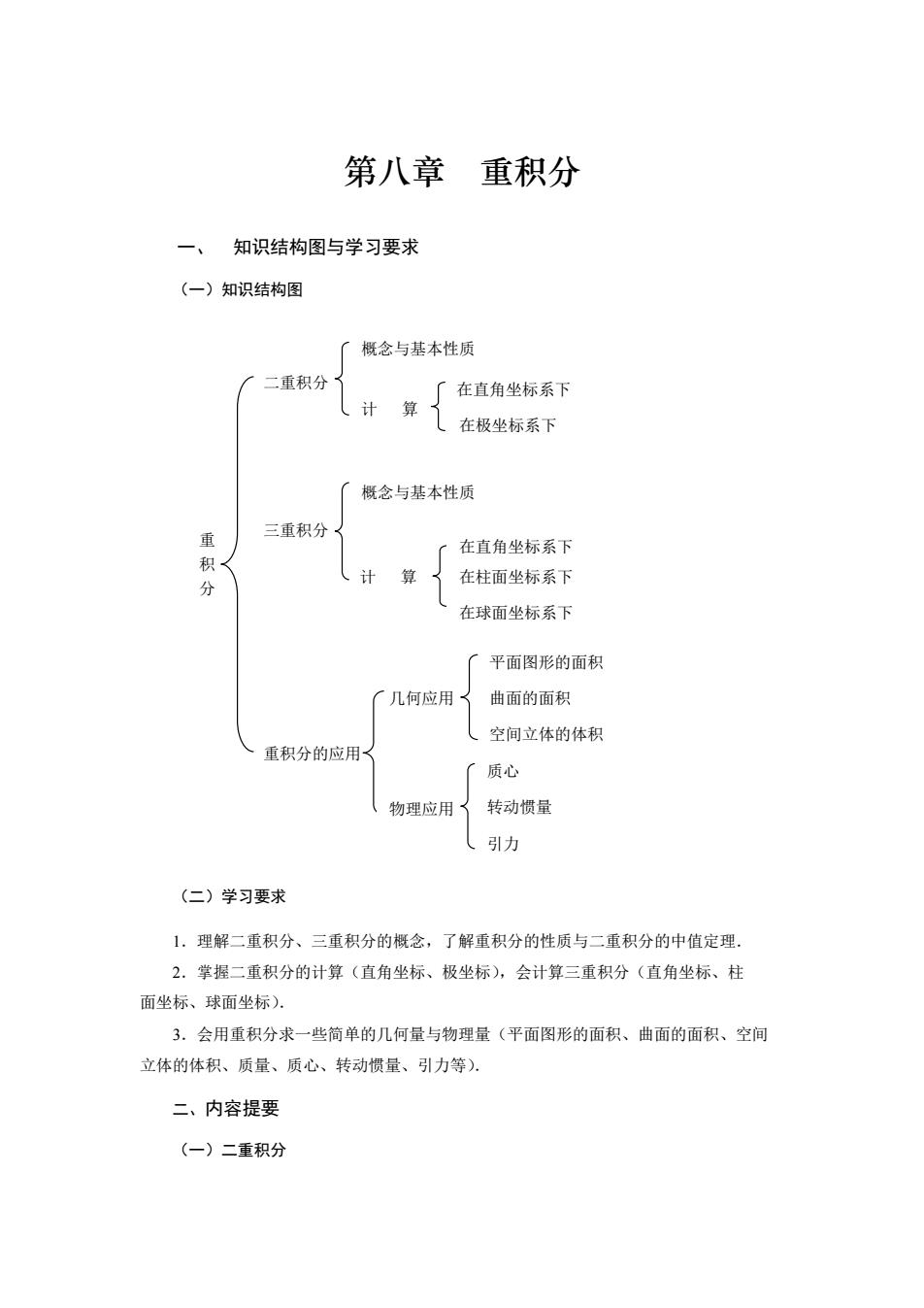
第八章 重积分 一、 知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解二重积分、三重积分的概念,了解重积分的性质与二重积分的中值定理. 2.掌握二重积分的计算(直角坐标、极坐标),会计算三重积分(直角坐标、柱 面坐标、球面坐标). 3.会用重积分求一些简单的几何量与物理量(平面图形的面积、曲面的面积、空间 立体的体积、质量、质心、转动惯量、引力等). 二、内容提要 (一)二重积分 重 积 分 重积分的应用 在直角坐标系下 计 算 转动惯量 曲面的面积 二重积分 平面图形的面积 质心 几何应用 计 算 空间立体的体积 物理应用 在极坐标系下 三重积分 概念与基本性质 在直角坐标系下 在柱面坐标系下 在球面坐标系下 概念与基本性质 引力

1.二重积分的定义∬fx,ydc=lim∑f5,n)Aa, 2.二重积分的几何意义 (1)若fx,)≥0,则∬fxdc表示以区域D为底、曲面:=fx)为曲顶的曲顶 柱体的体积. (2)若f优,)<0,则∬/x,y)do表示上述曲顶柱体体积的负值 (3)若x,)在区域D的部分区域上是正的,其它部分区域上是负的,则∬fx,yo 表示这些部分区域上的曲顶柱体体积的代数和 3.二重积分的物理意义 若面密度为p=fx,y)的平面薄片所占区域为D,则川f(x.y)da表示此薄片的质量。 4.二重积分的基本性质 (1)laxn士pg,圳da=ado±pj明gx,da,其中a,B为常数. (2)若D=DUD且DnD,=②,则j∬fx,ydo=∬fx,ydo+∬fx,do.(积 分区域的可加性) (3)若D的面积为a,则∬=o· 4)若在D上x川≤g则∬f化,do≤8xio.特别地, Ij∬fx,ydo小fx,y川do (5)若在闭区域D上m≤fx,y)≤M,o是D的面积,则om≤川/x,ydo≤oM. (6)(积分中值定理)若fx,)在闭区域D上连续,。为D的面积,则在D上存在 一点(5,使得∬fx,ydG=f5,a 5.二重积分的计算(化二重积分为二次积分进行计算) (1)在直角坐标系下计算时,厂f化,yo=川fx,y),且有 a.若D为X一型区域,即(x)≤y≤%(x),a≤x≤b,则 ∬f(x.yyda=fx,y. b.若D为Y一型区域,若,)≤x≤,O),c≤y≤d,则 [f(x.yda=广fxh
1.二重积分的定义 0 1 ( , ) lim ( , ) n i i i D i f x y d f → = = . 2.二重积分的几何意义 (1)若 f x y ( , ) 0, 则 ( , ) D f x y d 表示以区域 D 为底、曲面 z f x y = ( , ) 为曲顶的曲顶 柱体的体积. (2)若 f x y ( , ) 0 ,则 ( , ) D f x y d 表示上述曲顶柱体体积的负值. (3)若 f x y ( , ) 在区域 D 的部分区域上是正的,其它部分区域上是负的,则 ( , ) D f x y d 表示这些部分区域上的曲顶柱体体积的代数和. 3.二重积分的物理意义 若面密度为 = f x y ( , ) 的平面薄片所占区域为 D ,则 ( , ) D f x y d 表示此薄片的质量. 4.二重积分的基本性质 (1) ( , ) ( , ) ( , ) ( , ) , D D D f x y g x y d f x y d g x y d = 其中 , 为常数. (2)若 D D D = 1 2 且 D D 1 2 = ,则 1 2 ( , ) ( , ) ( , ) D D D f x y d f x y d f x y d = + .(积 分区域的可加性) (3)若 D 的面积为 ,则 D dxdy = . (4)若在 D 上 f x y g x y ( , ) ( , ), 则 ( , ) ( , ) D D f x y d g x y d .特别地, | ( , ) | | ( , ) | D D f x y d f x y d . (5)若在闭区域 D 上 m f x y M ( , ) , 是 D 的面积,则 ( , ) D m f x y d M . (6)(积分中值定理)若 f x y ( , ) 在闭区域 D 上连续, 为 D 的面积,则在 D 上存在 一点 ( , ), 使得 ( , ) ( , ) D f x y d f = . 5.二重积分的计算(化二重积分为二次积分进行计算) (1)在直角坐标系下计算时, ( , ) ( , ) D D f x y d f x y dxdy = ,且有 a.若 D 为 X -型区域,即 1 2 ( ) ( ) x y x , a x b ,则 2 1 ( ) ( ) ( , ) ( , ) b x a x D f x y d dx f x y dy = . b.若 D 为 Y -型区域,若 1 2 ( ) ( ) y x y ,c y d ,则 2 1 ( ) ( ) ( , ) ( , ) d y c y D f x y d dy f x y dx = .

(2)在极坐标系下计算时,根据直角坐标与极坐标的关系,即x=pcos0,y=psin8, d=pdpd,则有 (3)利用奇偶对称性化简二重积分 a.若区域D关于x轴对称,则 2[f(x,y)dd,f是关于的偶函数 ∬fx,y= 0, ∫是关于的奇函数 其中D,为区域D在上半平面y≥0或下半平面y≤0中的区域. b.若区域D关于y轴对称,则 2∬fx,)y,f是关于x的偶函数 fxy= 0 f是关于的奇函数 其中D,为区域D在右半平面x≥0或左半平面x≤0中的区域: c.若区域D关于原点对称,则 0, f是关于x或,的奇函数 其中D,为平面区域D在任意一个象限中的区域。 6.二重积分的应用 (1)曲项柱体的体积 以曲面:=x,)≥0(仁≥0)为曲顶、闭区域D为底的曲顶柱体的体积 r=∬fx,ydo. (2)曲面的面积 若曲面工为z=x,),Σ在xOy平面上的投影区域为D,则曲面Σ的面积 ++ (3)平面区域的面积 平面有界闭区域D的面积为 A=∬do (4)若平面薄片占有平面xO上的有界区域为D,其面密度函数为px,以,则 a.此海片的质量M=川p
(2)在极坐标系下计算时,根据直角坐标与极坐标的关系,即 x = cos ,y = sin , dxdy d d = ,则有 ( , ) ( cos , sin ) D D f x y d f d d = . (3)利用奇偶对称性化简二重积分 a.若区域 D 关于 x 轴对称,则 1 2 ( , ) , ( , ) 0, D D f x y dxdy f y f x y dxdy f y = 是关于 的偶函数 是关于 的奇函数 , 其中 D1 为区域 D 在上半平面 y 0 或下半平面 y 0 中的区域. b.若区域 D 关于 y 轴对称,则 2 2 ( , ) , ( , ) 0 D D f x y dxdy f x f x y dxdy f x = 是关于 的偶函数 , 是关于 的奇函数 , 其中 D2 为区域 D 在右半平面 x 0 或左半平面 x 0 中的区域; c.若区域 D 关于原点对称,则 3 4 ( , ) , ( , ) 0 D D f x y dxdy f x y f x y dxdy f x y = 是关于 和 的偶函数 , 是关于 或 的奇函数 , 其中 D3 为平面区域 D 在任意一个象限中的区域. 6.二重积分的应用 (1)曲顶柱体的体积 以曲面 z f x y z = ( , ) 0 ( 0) 为曲顶、闭区域 D 为底的曲顶柱体的体积 ( , ) D V f x y d = . (2)曲面的面积 若曲面 为 z z x y = ( , ), 在 xOy 平面上的投影区域为 D ,则曲面 的面积 2 2 1 ( ) ( ) D z z A dxdy x y = + + . (3)平面区域的面积 平面有界闭区域 D 的面积为 D A d = . (4)若平面薄片占有平面 xOy 上的有界区域为 D, 其面密度函数为 ( , ), x y 则 a.此薄片的质量 ( , ) D M x y d = .

b.此平面等片的质心坐标:=x0xda,了=xda,其中 M=川px,y)dc为此薄片的质量.特别地,均匀薄片的质心坐标为 =do,=打o,其中A=∬do c.此平面薄片对x轴和y轴的转动惯量分别为 ↓-Ppao,↓=∬p(x.ylda (二)三重积分 1,三重积分的定义 ∬fx,y=dw=lm∑f5,n,5)Au 2.三重积分的物理意义 ,y)20时,三重积分∬fx,y,)d加表示密度函数为fx,y,)的物体Q的质量。 3.三重积分的基本性质与二重积分的基本性质完全类似, 4.三重积分的计算(化三重积分为相应坐标系下的三次积分) (1)在直角坐标系下计算时,∬fx,y,:dw=∬fx,y,dt,且有如下计算 方法: a.“先一后二”法:假设平行于:轴且穿过闭区域Q内部的直线与闭区域Q的边界曲 面相交不多于两点,Q在xOy面上的投影为平面闭区域D,即 2={x,y(x,≤:≤(x,(x,eDn}。 多 fcdw=∬=t b.“先二后一”法:若Q={=x)ED,≤:≤G,其中D.是竖坐标为:的平面 截闭区域Ω所得的一个平面闭区域,则 Jj∬x,y=dw=正fxy=)h (2)在柱面坐标系下计算时,根据直角坐标与柱面坐标的关系,即x=Pcos0, y=psin0,:=z,可得 .x.-co.psin0.-pdpdod (3)在球面坐标系下计算时,根据直角坐标与球面坐标的关系,即x=rsinpcos0, y=rsinosin0,=rcoso,可得
b.此平面薄片的质心坐标: 1 ( , ) D x x x y d M = , 1 ( , ) D y y x y d M = ,其中 ( , ) D M x y d = 为此薄片的质量.特别地,均匀薄片的质心坐标为 1 D x xd A = , 1 D y yd A = ,其中 D A d = . c.此平面薄片对 x 轴和 y 轴的转动惯量分别为 2 ( , ) x D I y x y d = , 2 ( , ) y D I x x y d = . (二)三重积分 1.三重积分的定义 f x y z d ( , , ) 0 1 lim ( , , ) n i i i i i f → = = . 2.三重积分的物理意义 f x y z ( , , ) 0 时,三重积分 f x y z d ( , , ) 表示密度函数为 f x y z ( , , ) 的物体 的质量. 3.三重积分的基本性质与二重积分的基本性质完全类似. 4.三重积分的计算(化三重积分为相应坐标系下的三次积分) (1)在直角坐标系下计算时, f x y z d f x y z dxdydz ( , , ) ( , , ) = ,且有如下计算 方法: a.“先一后二”法:假设平行于 z 轴且穿过闭区域 内部的直线与闭区域 的边界曲 面相交不多于两点, 在 xOy 面上的投影为平面闭区域 D xy ,即 1 2 {( , , ) ( , ) ( , ),( , ) }, xy = x y z z x y z z x y x y D 则 2 1 ( , ) ( , ) ( , , ) ( , , ) . xy z x y z x y D f x y z d dxdy f x y z dz = b.“先二后一”法:若 1 2 {( , , ) ( , ) , }, z = x y z x y D c z c 其中 D z 是竖坐标为 z 的平面 截闭区域 所得的一个平面闭区域,则 2 1 ( , , ) ( , , ) z c c D f x y z d dz f x y z dxdy = . (2)在柱面坐标系下计算时,根据直角坐标与柱面坐标的关系,即 x = cos , y = sin , z z = ,可得 f x y z d f z d d dz ( , , ) ( cos , sin , ) = . (3)在球面坐标系下计算时,根据直角坐标与球面坐标的关系,即 x r = sin cos , y r = sin sin , z r = cos ,可得

f(x.y.d-F(.sindrdod0. 其中Fc,o,)=f(rsincos0,rsinsin0,rcosp) (4)利用奇偶对称性化简三重积分 a.若积分区域Q关于平面x=0对称,则 2∬f(x.y.=)dv,∫是关于的偶函数时 订fx,ydo= 0, ∫是关于的奇函数时 其中2,为区域2中x≥0的区域: b.若积分区域2关于平面y=0对称,则 2∬fx,y)do,f是关于的偶函数时 ∬xydw= o. ∫是关于的奇函数时 其中2,为区域2中y≥0的区域: c.若积分区域Q关于平面:=0对称,则 2川fx,y,)dw,∫是关于:的偶函数时 ∬xyd= ∫是关于的奇函数时 其中2,为区域2中:20的区域. 5.三重积分的应用 (1)立体体积 若立体所占空间区域为2,则其体积 v=dv. (2)物体质量 若物体所占空间区域为,密度函数为(x,),则其质量 M=p(x.y.=)do. (3)物体的质心坐标 物体所占空间区域为Q,密度函数为(x,少,=),则其质心坐标为 四o恤,-立为:a顶=pxxw.其中 M=P,为此物体的质量。 (4)物体的转动惯量 上述物体对x轴、y轴、:轴的转动惯量分别为
2 f x y z d F r r drd d ( , , ) ( , , ) sin = , 其中 F r( , , ) = f r r r ( sin cos , sin sin , cos ) . (4)利用奇偶对称性化简三重积分 a.若积分区域 关于平面 x = 0 对称,则 1 2 ( , , ) , ( , , ) 0, f x y z d f x f x y z d f x = 是关于 的偶函数时 是关于 的奇函数时 , 其中 1 为区域 中 x 0 的区域; b. 若积分区域 关于平面 y = 0 对称,则 1 2 ( , , ) , ( , , ) 0, f x y z d f y f x y z d f y = 是关于 的偶函数时 是关于 的奇函数时 , 其中 1 为区域 中 y 0 的区域; c.若积分区域 关于平面 z = 0 对称,则 1 2 ( , , ) , ( , , ) 0, f x y z d f z f x y z d f z = 是关于 的偶函数时 是关于 的奇函数时 , 其中 1 为区域 中 z 0 的区域. 5. 三重积分的应用 (1)立体体积 若立体所占空间区域为 ,则其体积 V d = . (2)物体质量 若物体所占空间区域为 ,密度函数为 ( , , ) x y z ,则其质量 M x y z d ( , , ) = . (3)物体的质心坐标 物体所占空间区域为 ,密度函数为 ( , , ) x y z ,则其质心坐标为 1 x x x y z d ( , , ) , M = 1 y y x y z d ( , , ) , M = 1 z z x y z d ( , , ) M = .其中 M x y z d ( , , ) = 为此物体的质量. (4)物体的转动惯量 上述物体对 x 轴、 y 轴、 z 轴的转动惯量分别为

1=J∬0+2px,dw,=j∬r+产)px,yd,1=∬x+y)p(x.y.=dv (5)物体对质点的引力 设质量为册的质点位于点P(,水。,)处,物体所占空间区域为Q,其密度函数为 pxy,),则物体对质点的引力为F={5,5,E},其中 E=G∬xy=)d,5=Gjxx=)'”aw,R=Gj0xy=)产dw, 式中r=x-x}+0y-6广+-了,G为引力常数
2 2 ( ) ( , , ) x I y z x y z d = + , 2 2 ( ) ( , , ) y I x z x y z d = + , 2 2 ( ) ( , , ) z I x y x y z d = + . (5)物体对质点的引力 设质量为 m 的质点位于点 0 0 0 0 P x y z ( , , ) 处,物体所占空间区域为 ,其密度函数为 ( , , ), x y z 则物体对质点的引力为 { , , } F = F F F x y z ,其中 0 3 ( , , ) x x x F G x y z d r − = , 0 3 ( , , ) y y y F G x y z d r − = , 0 3 ( , , ) z z z F G x y z d r − = , 式中 2 2 2 0 0 0 r x x y y z z = − + − + − ( ) ( ) ( ) , G 为引力常数.