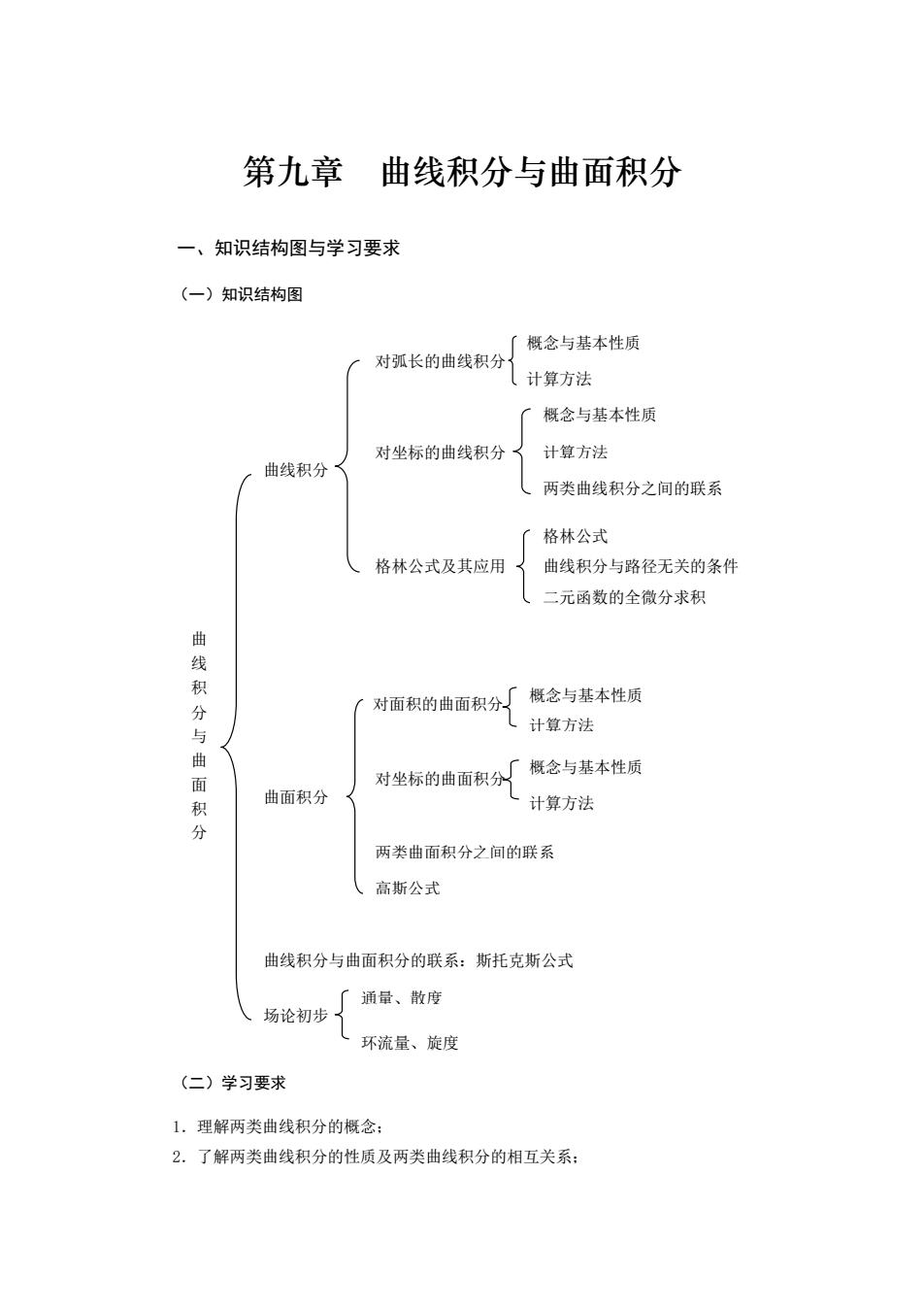
第九章曲线积分与曲面积分 一、知识结构图与学习要求 (一)知识结构图 概念与基本性质 对弧长的曲线积分 计算方法 概念与基本性质 对坐标的曲线积分 计算方法 曲线积分 两类曲线积分之间的联系 格林公式 格林公式及其应用 曲线积分与路径无关的条件 二元函数的全微分求积 曲线 对面积的曲面积分厂概念与基本性质 分与曲 儿计算方法 对坐标的曲面积分厂概念与基本性质 曲面积分 计算方法 两类曲面积分之间的联系 (高斯公式 曲线积分与曲面积分的联系:斯托克斯公式 场论初步量、府 环流量、旋度 (二)学习要求 1.理解两类曲线积分的概念: 2.了解两类曲线积分的性质及两类曲线积分的相互关系:
第九章 曲线积分与曲面积分 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解两类曲线积分的概念; 2.了解两类曲线积分的性质及两类曲线积分的相互关系; 曲 线 积 分 与 曲 面 积 分 曲面积分 计算方法 计算方法 曲线积分 对面积的曲面积分 对坐标的曲面积分 对弧长的曲线积分 两类曲线积分之间的联系 概念与基本性质 格林公式及其应用 曲线积分与路径无关的条件 对坐标的曲线积分 概念与基本性质 概念与基本性质 概念与基本性质 计算方法 计算方法 高斯公式 两类曲面积分之间的联系 场论初步 二元函数的全微分求积 格林公式 通量、散度 环流量、旋度 曲线积分与曲面积分的联系:斯托克斯公式

3。熟练掌握两类曲线积分的计算: 4.理解格林公式并会运用平面曲线积分与路径无关的条件,会求全微分的原函数: 5.了解两类曲面积分的概念、性质及两类曲面积分的关系,掌握计算两类曲面积分 的方法,会用高斯公式、斯托克斯公式计算曲面积分: 6.了解散度与旋度的概念,并会计算: 7.会用曲线积分和曲面积分求一些几何量和物理量(曲面面积、弧长、质量、重心、 转动惯量、引力、功及流量等) 二、内容提要 (一)曲线积分 1,对孤长的曲线积分(第一类曲线积分) (1)设L是xOy面内的一条光滑曲线弧,函数fx,)在L上有界,则定义在L上对 弧长的曲线积分为 xh=m之G.m 当fc,)=1时,∫本表示曲线L的弧长. 若是空间的一条曲线,可以类似平面的情形,对弧长的曲线积分定义为 =出=g26,5A 当fx,y)=1时,∫本表示空间曲线Γ的弧长。 (2)当L的参数方程为上=0 r=w0’as1s,则 ,fx,yd=f几0,wNp()+w0t,(a≤B). U=a≤r≤,则 当曲线L的方程为y=y(Xa≤x≤b),可将L的参数方程设为= Jxy达=∫fx,wxN+wxr本. 当曲线L的方程为x=9 vXcsysd小,可将L的参数方程设为=》(esysd小,则 (y=y Jfx,达=厂f以,voor+1d 注计算第一类曲线积分时,将曲线积分化为定积分时,要注意定积分的上限要不小
3.熟练掌握两类曲线积分的计算; 4.理解格林公式并会运用平面曲线积分与路径无关的条件,会求全微分的原函数; 5.了解两类曲面积分的概念、性质及两类曲面积分的关系,掌握计算两类曲面积分 的方法,会用高斯公式、斯托克斯公式计算曲面积分; 6.了解散度与旋度的概念,并会计算; 7.会用曲线积分和曲面积分求一些几何量和物理量(曲面面积、弧长、质量、重心、 转动惯量、引力、功及流量等). 二、内容提要 (一)曲线积分 1.对弧长的曲线积分(第一类曲线积分) (1) 设 L 是 xOy 面内的一条光滑曲线弧,函数 f x y ( , ) 在 L 上有界,则定义在 L 上对 弧长的曲线积分为 0 1 ( , ) lim ( , ) n i i i L i f x y ds f s → = = . 当 f x y ( , ) 1 时, L ds 表示曲线 L 的弧长. 若 是空间的一条曲线,可以类似平面的情形,对弧长的曲线积分定义为 0 1 ( , , ) lim ( , , ) n i i i i L i f x y z ds f s → = = . 当 f x y z ( , , ) 1 时, L ds 表示空间曲线 的弧长. (2)当 L 的参数方程为 ( ) ( ) x t y t = = , t ,则 2 2 ( , ) [ ( ), ( )] ( ) ( ) L f x y ds f t t t t dt = + ,( ). 当曲线 L 的方程为 y x a x b = ( )( ) ,可将 L 的参数方程设为 ( ) x x y x = = ( ) a x b ,则 2 ( , ) [ , ( )] 1 [ ( )] b L a f x y ds f x x x dx = + . 当曲线 L 的方程为 x y c y d = ( )( ) ,可将 L 的参数方程设为 x y( ) y y = = ( ) c y d ,则 2 ( , ) [ ( ), ] [ ( )] 1 d L c f x y ds f y y y dy = + . 注 计算第一类曲线积分时,将曲线积分化为定积分时,要注意定积分的上限要不小

于下限. (3)物理意义 设曲线L的线密度为p(x,),则其质量为M=∫,P(x,y达· 2.对坐标的曲线积分(第二类曲线积分) (1)设L为xOy面内从点A到B的一条有向光滑曲线弧,函数P(x,)、Qx,)在L上 有界.则定义函数Px,)在有向曲线弧L上对坐标x的曲线积分为 PG.(A 类似可以定义对坐标y的曲线积分为∫Q(x)=m∑Q5,n,)4y·常见的还有如下的组 合形式 [P(x.y)dx+(x.y)dy =P(x.y)d+(x.y)dy 注对坐标的曲线积分与积分曲线的方向有关,设[表示L的反向曲线弧,则 SP(x.y)d+O(x,y)dy=-P(x.y)dx+Q(x.y)dy (2)当曲线L的参数方程为=,且当:由口变化到B时,曲线L由A变化到B y=0 ∫Px,yd+x,yd=∫{P(x,r)+(a),by')d 当曲线L的方程为y=),可将L的参数方程设为 =闭’从a变化到6,则 P(x.y+(x.y)dy =(P[x.(x+(x.M(x)l(x)d 若线L的方为=试0小,可格L的参数方程设为:.少从e变化,圆 [.P(x.y)dx+Q(x.y)dy =[(PIx(y).yl(y)+a(x(y).y]dy. 同理可以定义三元函数fx,y,)在空间曲线「上对坐标x,y和:的曲线积分,并有相应 的计算方法. 注在计算此类曲线积分时候,积分下限值对应于曲线的起点的参数值,积分上限值对 应于曲线的终点的参数值,上限值不一定大于下限值。 3.两类曲线积分之间的关系 (1)平面曲线L的情形: P(xd+(x)dy=[P(x.y)cosa+(y)cos plds
于下限. (3)物理意义 设曲线 L 的线密度为 (x, y) ,则其质量为 ( , ) L M x y ds = . 2.对坐标的曲线积分(第二类曲线积分) (1)设 L 为 xOy 面内从点 A 到 B 的一条有向光滑曲线弧,函数 P x y ( , ) 、Q x y ( , ) 在 L 上 有界.则定义函数 P x y ( , ) 在有向曲线弧 L 上对坐标 x 的曲线积分为 0 1 ( , ) lim ( , ) n i i i L i P x y dx P x → = = , 类似可以定义对坐标 y 的曲线积分为 0 1 ( , ) lim ( , ) n i i i L i Q x y dy Q y → = = .常见的还有如下的组 合形式 ( , ) ( , ) L P x y dx Q x y dy + ( , ) ( , ) L L = + P x y dx Q x y dy . 注 对坐标的曲线积分与积分曲线的方向有关,设 L − 表示 L 的反向曲线弧,则 ( , ) ( , ) ( , ) ( , ) L L P x y dx Q x y dy P x y dx Q x y dy − + = − + . (2)当曲线 L 的参数方程为 ( ) ( ) x x t y y t = = ,且当 t 由 变化到 时,曲线 L 由 A 变化到 B , 则 ( , ) ( , ) L P x y dx Q x y dy + = { [( ( ), ( )] ( ) [( ( ), ( )] ( )} P x t y t x t Q x t y t y t dt + . 当曲线 L 的方程为 y y x = ( ) ,可将 L 的参数方程设为 ( ) x x y y x = = , x 从 a 变化到 b ,则 ( , ) ( , ) L P x y dx Q x y dy + { [ , ( )] [( , ( )] ( )} b a = + P x y x Q x y x y x dx . 若曲线 L 的方程为 x x y = ( ) ,可将 L 的参数方程设为 x x y( ) y y = = , y 从 c 变化到 d ,则 ( , ) ( , ) L P x y dx Q x y dy + { [ ( ), ] ( ) [( ( ), ]} . d c = + P x y y x y Q x y y dy 同理可以定义三元函数 f x y z ( , , ) 在空间曲线 上对坐标 x y, 和 z 的曲线积分,并有相应 的计算方法. 注 在计算此类曲线积分时候,积分下限值对应于曲线的起点的参数值,积分上限值对 应于曲线的终点的参数值,上限值不一定大于下限值. 3.两类曲线积分之间的关系 (1)平面曲线 L 的情形: ( , ) ( , ) [ ( , )cos ( , )cos ] L L P x y dx Q x y dy P x y Q x y ds + = +

其中csa,c0sB为有向曲线L上点(x,)处的切向量的方向余弦 (2)空间曲线厂的情形: Pxyh+Qx,八+Rxyt =[P(x.y,=)cosa+Q(x.y,=)cos B+R(x.y,=)cosylds, 其中cosa,cosB,cosy为有向曲线「上点(x,八,:)处的切向量的方向余弦. 4.格林公式、曲线积分与路径无关的条件 (1)格林公式 设平面闭区域D由分段光滑的曲线L围成,函数P(x,),Q(x,)在D上具有一阶连续 偏导数,则有 其中L是D的取正向的边界曲线, (2)积分与路径无关的条件 设P(x,以,Qx,)在单连通区域D内有连续的一阶偏导数,则下列四个命题等价: a.∫P红,d+O(x,)在D内积分与路径无关: b.∮Px+O(x,)=0,L为D内任一闭曲线 c器-nen: d.存在可微函数ux,),使得d=Px,y)t+Qx,yd,且有 x.P+ =O,d+广Px, 其中(3%)为D内任一点. 5.两类曲线积分的应用 (1)利用曲线积分求弧长s=」d心. (2)利用曲线积分求重心坐标 设空间曲线「的线密度函数为(x,y,),则重心坐标(区,以)可由下式给出,即 其中M=[4(x乃,). (3)求转动惯量
其中 cos ,cos 为有向曲线 L 上点 ( , ) x y 处的切向量的方向余弦. (2)空间曲线 的情形: ( , , ) ( , , ) ( , , ) L P x y z dx Q x y z dy R x y z dz + + [ ( , , )cos ( , , )cos ( , , )cos ] L = + + P x y z Q x y z R x y z ds , 其中 cos ,cos ,cos 为有向曲线 上点 ( , , ) x y z 处的切向量的方向余弦. 4.格林公式、曲线积分与路径无关的条件 (1)格林公式 设平面闭区域 D 由分段光滑的曲线 L 围成,函数 P x y ( , ) ,Q x y ( , ) 在 D 上具有一阶连续 偏导数,则有 ( ) L D Q P dxdy Pdx Qdy x y − = + , 其中 L 是 D 的取正向的边界曲线. (2)积分与路径无关的条件 设 P x y Q x y ( , ), ( , ) 在单连通区域 D 内有连续的一阶偏导数,则下列四个命题等价: a. ( , ) ( , ) L P x y dx Q x y dy + 在 D 内积分与路径无关; b. ( , ) ( , ) 0 L P x y dx Q x y dy + = , L 为 D 内任一闭曲线; c. ,( , ) Q P x y D x y = ; d.存在可微函数 u x y ( , ) ,使得 du P x y dx Q x y dy = + ( , ) ( , ) ,且有 0 0 0 0 ( , ) 0 ( , ) ( , ) ( , ) ( , ) x y x y x y x y u x y Pdx Qdy P x y dx Q x y dy = + = + 0 0 0 ( , ) ( , ) y x y x = + Q x y dy P x y dy , 其中 0 0 ( , ) x y 为 D 内任一点. 5.两类曲线积分的应用 (1)利用曲线积分求弧长 L s ds = . (2)利用曲线积分求重心坐标 设空间曲线 的线密度函数为 ( , , ) x y z ,则重心坐标 ( , , ) x y z 可由下式给出,即 1 x x y z xds ( , , ) M = , 1 y x y z yds ( , , ) M = , 1 z x y z zds ( , , ) M = , 其中 M x y z ds ( , , ) = . (3)求转动惯量

设平面曲线弧L上任意一点(x,)处的线密度为p(x,),则绕x轴、y轴和原点的转动 惯量分别为 1,=p(x.y)yids,I=p(x.y)x'ds,lo=S p(x.yxi+y')ds. 设空间曲线弧「上任意一点(x,八,)处的线密度为xy,),则绕x轴、y轴、:轴和原 点的转动惯量分别为 1=xyX0y+2达,1,=x,y=x2+2达 12=∫px,y,x2+y2d, lo=fp(x.y.x++:ds (4)变力沿曲线做功 设变力F=P(x,)i+Qx,yi,则变力沿平面曲线L所作的功为 W=∫Px,yh+Ox,y 同理可利用对坐标的曲线积分求变力沿空间曲线所作的功, (二)曲面积分 1.对面积的曲面积分(第一类曲面积分) (1)设曲面Σ是光滑的,函数∫(x,y,)在上有界.则定义函数x,y,:)在曲面Σ上 对面积的曲面积分为 jfx,ys=im∑f5,n,5)As 称dS为曲面面积元素,且曲面Σ的面积为川dS. (2)当曲面Σ由方程z=(x,y)给出,Σ在xOy面上的投影区域为Dm,函数z=(x,y) 在D,上具有连续偏导数,被积函数fx八)在Σ上连续,则 ∬fx==∬几x红++d D 当积分曲面Σ的方程为y=(x,),D为Σ在Ox面上的投影区域,则函数fx,y,)在Σ 上对面积的曲面积分为 ∬fxys=∬几x,e,xW+e,x)+ye,xt。 当积分曲面Σ的方程为x=x(y,),D-为2在O:面上的投影尽域,则函数fx,y)在 上对面积的曲面积分为
设平面曲线弧 L 上任意一点 ( , ) x y 处的线密度为 ( , ) x y , 则绕 x 轴、 y 轴和原点的转动 惯量分别为 2 ( , ) x L I x y y ds = , 2 ( , ) y L I x y x ds = , 2 2 ( , )( ) O L I x y x y ds = + . 设空间曲线弧 上任意一点 ( , , ) x y z 处的线密度为 ( , , ) x y z ,则绕 x 轴、 y 轴、 z 轴和原 点的转动惯量分别为 2 2 ( , , )( ) x I x y z y z ds = + , 2 2 ( , , )( ) y I x y z x z ds = + , 2 2 ( , , )( ) z I x y z x y ds = + , 2 2 2 ( , , )( ) O I x y z x y z ds = + + . (4)变力沿曲线做功 设变力 F i j = + P x y Q x y ( , ) ( , ) ,则变力沿平面曲线 L 所作的功为 ( , ) ( , ) L W P x y dx Q x y dy = + . 同理可利用对坐标的曲线积分求变力沿空间曲线所作的功. (二)曲面积分 1.对面积的曲面积分(第一类曲面积分) (1)设曲面 是光滑的,函数 f x y z ( , , ) 在 上有界.则定义函数 f x y z ( , , ) 在曲面 上 对面积的曲面积分为 0 1 ( , , ) lim ( , , ) n i i i i i f x y z dS f S → = = . 称 dS 为曲面面积元素,且曲面 的面积为 dS . (2)当曲面 由方程 z z x y = ( , ) 给出, 在 xOy 面上的投影区域为 D xy ,函数 z z x y = ( , ) 在 D xy 上具有连续偏导数,被积函数 f x y z ( , , ) 在 上连续 则 2 2 ( , , ) [ , , ( , )] 1 ( , ) ( , ) xy x y D f x y z dS f x y z x y z x y z x y dxdy = + + . 当积分曲面 的方程为 y y x z = ( , ) ,D xz 为 在 zOx 面上的投影区域 则函数 f x y z ( , , ) 在 上对面积的曲面积分为 2 2 ( , , ) [ , ( , ), ] 1 ( , ) ( , ) zx z x D f x y z dS f x y z x z y z x y z x dzdx = + + . 当积分曲面 的方程为 x x y z = ( , ),D yz 为 在 yOz 面上的投影区域,则函数 f x y z ( , , ) 在 上对面积的曲面积分为

∬fxys=川几0,yV+x0y)+x0yt (3)当x,y,)≥0时,对面积的曲面积分∫川∫x,y,:)S在物理上表示面密度函数为 p=f(x,水,)的曲面物体的质量。 2.对坐标的曲面积分(第二类曲面积分) (1)设工为光滑的有向曲面,函数R(x,八,)在工上有界.则定义函数(x八,)在有向 曲面Σ上对坐标x、y的曲面积分为 ∬Rx,y=lim∑R5,n,5AS 类似地可定义 ∬Pxy=t=lm∑P5,n,S△S ∬e(x,y,=dd=lim∑0(5,n,5aS)a 通常将到∬Px,y,=dt+∬Q(x,y,=dd+∬Rx,y,=d简记为 ∬Px,y,)dt+O(x,y,)tk+Rx,y,=d。 注对坐标的曲面积分与积分曲面的侧(即取定的法向量)有关,即 ∬Pdt+Od-ds+Rdd=-J∬Pdt+Od-dx+Rdk 其中Σ表示与Σ相反侧的有向曲面. (2)当积分曲面Σ由方程:=(x,y)给出,Σ在xO面上的投影区域为D。,则有 x,y,dd=∬xy(xytd, 其中当Σ取上侧时(即Σ的法向量与:轴正向的夹角成锐角),积分前取“+”;当Σ取下侧 时(即Σ的法向量与:轴正向的夹角成钝角),积分前取“-” 类似地,如果Σ由x=x(y,)给出,则有 Px,yt=∬Pxyt 如果Σ由y=(x,)给出,则有 ∬Q(xy,)td=±Q[x,e,xd 其中符号由曲面的法向量与y轴正向的夹角或与x轴正向的夹角来确定,原则是“锐角为正, 纯角为负” 3.两类曲面积分之间的关系 ∬PMt+Oth+R-∬Poosa++Rcos7达, 其中cosa,cOsB,cosy是有向曲面Σ上点(x,y,)处的法向量的方向余弦
2 2 ( , , ) [ ( , ), , ] 1 ( , ) ( , ) yz y z D f x y z dS f x y z y z x y z x y z dydz = + + . (3)当 f x y z ( , , ) 0 时,对面积的曲面积分 f x y z dS ( , , ) 在物理上表示面密度函数为 = f x y z ( , , ) 的曲面物体的质量. 2.对坐标的曲面积分(第二类曲面积分) (1)设 为光滑的有向曲面,函数 R x y z ( , , ) 在 上有界.则定义函数 R x y z ( , , ) 在有向 曲面 上对坐标 x 、 y 的曲面积分为 0 1 ( , , ) lim ( , , )( ) n i i i i xy i R x y z dxdy R S → = = . 类似地可定义 0 1 ( , , ) lim ( , , )( ) n i i i i yz i P x y z dydz P S → = = , 0 1 ( , , ) lim ( , , )( ) n i i i i zx i Q x y z dzdx Q S → = = . 通常将 P x y z dydz Q x y z dzdx R x y z dxdy ( , , ) ( , , ) ( , , ) + + 简记为 P x y z dydz Q x y z dzdx R x y z dxdy ( , , ) ( , , ) ( , , ) + + . 注 对坐标的曲面积分与积分曲面的侧(即取定的法向量)有关,即 Pdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy − + + = − + + , 其中 − 表示与 相反侧的有向曲面. (2)当积分曲面 由方程 z z x y = ( , ) 给出, 在 xOy 面上的投影区域为 D xy ,则有 ( , , ) [ , , ( , )] Dxy R x y z dxdy R x y z x y dxdy = , 其中当 取上侧时(即 的法向量与 z 轴正向的夹角成锐角),积分前取“+” 当 取下侧 时(即 的法向量与 z 轴正向的夹角成钝角),积分前取“−”. 类似地,如果 由 x x y z = ( , ) 给出,则有 ( , , ) [ ( , ), , ] Dyz P x y z dydz P x y z y z dydz = . 如果 由 y y x z = ( , ) 给出,则有 ( , , ) [ , ( , ), ] Dzx Q x y z dzdx Q x y z x z dzdx = , 其中符号由曲面的法向量与 y 轴正向的夹角或与 x 轴正向的夹角来确定,原则是“锐角为正, 钝角为负”. 3.两类曲面积分之间的关系 Pdydz Qdzdx Rdxdy P Q R dS ( cos cos cos ) + + = + + , 其中 cos ,cos ,cos 是有向曲面 上点 ( , , ) x y z 处的法向量的方向余弦.

4.两类曲面积分的应用 设为空间曲面,曲面上任意一点(x,y,)处的面密度为(x,y,),则 ()空间曲面薄片Σ的面积A=川S,其中A为曲面Σ的面积。 (2)曲面薄片Σ绕x轴、y轴、:轴和原点的转动惯量分别为 1=∬pxy2+s,,=∬o(x.y.=Xx2+ 1.=j∬px,y,x2+y2),o=∬px,y,x2+y2+2ds. (3)曲面薄片Σ的质量 M=∬pxy=)s (4)若曲面薄片Σ的重心坐标G元,),则有 y.ds.sx.y.)ds. 5.高斯公式 设空间闭区域2是由分片光滑的闭曲面Σ所围成,函数P(x,y,)、O(x,以,)、R(x,y,) 在Ω上具有一阶连续偏导数,则有如下公式(即高斯公式)成立: +器+器h-每t+Q+, 小g+号+警h=Poaa+QsA+Rasr, 这里Σ是2的整个边界曲面的外侧,cosa,cosB,cosy是有向曲面Σ上点(x,y,)处的法向 量的方向余弦. 6.斯托克斯公式 设Γ为分段光滑的空间有向闭曲线,Σ是以「为边界的分片光滑的有向曲面,「的正向 与Σ的侧符合右手规则,函数P(x,y,)、Qx,)、xy,)在曲面Σ(连同边界)上具有 一阶连续偏导数,则有如下公式(即斯托克斯公式)成立: 小受t+是股器器h-P+Q+肚。 或记为 ht止tdkd 品号是f++, P O R
4.两类曲面积分的应用 设 为空间曲面,曲面上任意一点 ( , , ) x y z 处的面密度为 ( , , ) x y z ,则 (1)空间曲面薄片 的面积 A dS = ,其中 A 为曲面 的面积. (2)曲面薄片 绕 x 轴、 y 轴、 z 轴和原点的转动惯量分别为 2 2 ( , , )( ) x I x y z y z dS = + , 2 2 ( , , )( ) y I x y z x z dS = + , 2 2 ( , , )( ) z I x y z x y dS = + , 2 2 2 ( , , )( ) O I x y z x y z dS = + + . (3)曲面薄片 的质量 M x y z dS ( , , ) = . (4)若曲面薄片 的重心坐标 G x y z ( , , ) ,则有 1 x x y z xdS ( , , ) M = , 1 y x y z ydS ( , , ) M = , 1 z x y z zdS ( , , ) M = . 5.高斯公式 设空间闭区域 是由分片光滑的闭曲面 所围成,函数 P x y z ( , , ) 、Q x y z ( , , ) 、R x y z ( , , ) 在 上具有一阶连续偏导数,则有如下公式(即高斯公式)成立: ( ) P Q R dv Pdydz Qdzdx Rdxdy x y z + + = + + , 或 ( ) ( cos cos cos ) P Q R dv P Q R dS x y z + + = + + , 这里 是 的整个边界曲面的外侧, cos ,cos ,cos 是有向曲面 上点 ( , , ) x y z 处的法向 量的方向余弦. 6.斯托克斯公式 设 为分段光滑的空间有向闭曲线, 是以 为边界的分片光滑的有向曲面, 的正向 与 的侧符合右手规则,函数 P x y z ( , , ) 、Q x y z ( , , ) 、R x y z ( , , ) 在曲面 (连同边界)上具有 一阶连续偏导数,则有如下公式(即斯托克斯公式)成立: dxdy y P x Q dzdx x R z P dydz z Q y R ( ) ( ) ( ) − + − + − = Pdx+Qdy +Rdz . 或记为: dydz dzdx dxdy Pdx Qdy Rdz x y z P Q R = + +

cosa cosB cosy Pdx+Qdy+Rd P R 其中cosa,c0sB,cosy是有向曲面Σ上点(:,少)处的法向量的方向余弦 (三)通量、散度、环流量与旋度 设有向量场A=Px,y,=+0(x水,=+Rx,y,=k,其中P(xy,)),Q(x火,=)和 R(x,y,:)具有一阶连续偏导数,Σ是场内的一有向曲面,n={co0sa,cosB,cos》是Σ上指定 侧的单位法向量. 1.向量场A通过曲面Σ向者指定侧的通量(或流量) J∬AndS=∬(Pcosa+QcosB+Rcosy)d=∬Pdt+Ot+Rhd 2.向量场A的散度 div A=OP00 OR ax ay 3.向量场A的旋度 P Q R 4.向量场A沿闭曲线厂的环流量 ∮Pt+O+Rt=∮AS, 其中1是「上点(化以)处的单位切向量
或 cos cos cos Pdx Qdy Rdz x y z P Q R = + + , 其中 cos ,cos ,cos 是有向曲面 上点 ( , , ) x y z 处的法向量的方向余弦. (三)通量、散度、环流量与旋度 设 有 向 量 场 A i j k = + + P x y z Q x y z R x y z ( , , ) ( , , ) ( , , ) , 其 中 P x y z ( , , ) , Q x y z ( , , ) 和 R x y z ( , , ) 具有一阶连续偏导数, 是场内的一有向曲面, n ={cos ,cos ,cos } 是 上指定 侧的单位法向量. 1.向量场 A 通过曲面 向着指定侧的通量(或流量) dS P Q R dS ( cos cos cos ) = + + A n = Pdydz Qdzdx Rdxdy + + 2.向量场 A 的散度 div PQR x y z = + + A . 3.向量场 A 的旋度 ( ) ( ) ( ) R Q P R Q P y z z x x y = − + − + − rot A i j k x y z P Q R = i j k . 4.向量场 A 沿闭曲线 的环流量 Pdx Qdy Rdz dS + + = A t , 其中 t 是 上点 ( , , ) x y z 处的单位切向量.