
第一章 函数与极限 函数是现代数学的基本概念之一,是高等 数学的主要研究对象。极限概念是微积分的 理论基础,极限方法是微积分的基本分析方 法,因此掌握、运用好极限方法是学好微积 分的关键。连续是函数的一个重要性态。本 章介绍映射、函数、极限和函数的连续性等 基本概念以及它们的一些性质。 素山医学院信息工程学院高等数学教研室

第一节映射与函数 (Mapping and Function) 一问题的提出 二 函数基本概念 三 函数的几种特性 四五 复合函数、反函数 小结与思考判断题 泰山医学院信息工程学院高等数学教研室 2

问题的提出 微积分是一门以变量为研究对象、 以极限方法作为研究工具的数学学 科,应用极限方法研究各类变化率问 题和几何学中曲线的切线问题,就产 生了微分学;应用极限方法研究诸如 曲边梯形的面积等涉及到微小量无穷 积累的问题,就产生了积分学。英国 数学家牛顿和德国数学家莱布尼兹同 时发现了微积分,微积分研究的主要 对象就是函数。 素山医学院信息工程学院高等数学教研室

二、集合(Set):创始人:德国数学家康托尔 1.集合概念 我们把具有某种特定性质的事物所组 成的总体称为一个集合。 组成这个集合的事物称为该集合的元素。 A={a1,a2,.,un} M={xx所具有的特征}a∈M,aEM, 注:集合的表示方法主要有列举法和描述法。 素山医学院信息工程学院高等数学教研室

2、集合的运算 并:AUB-{xx∈A或x∈B} 交:AOB={xx∈A且x∈B} 差:AIB={xx∈A且xEB} 补:A={x∈且xEA} A与B的直积:A×B={(x,y)x∈A且y∈B 素山医学院信息工程学院高等数学教研室
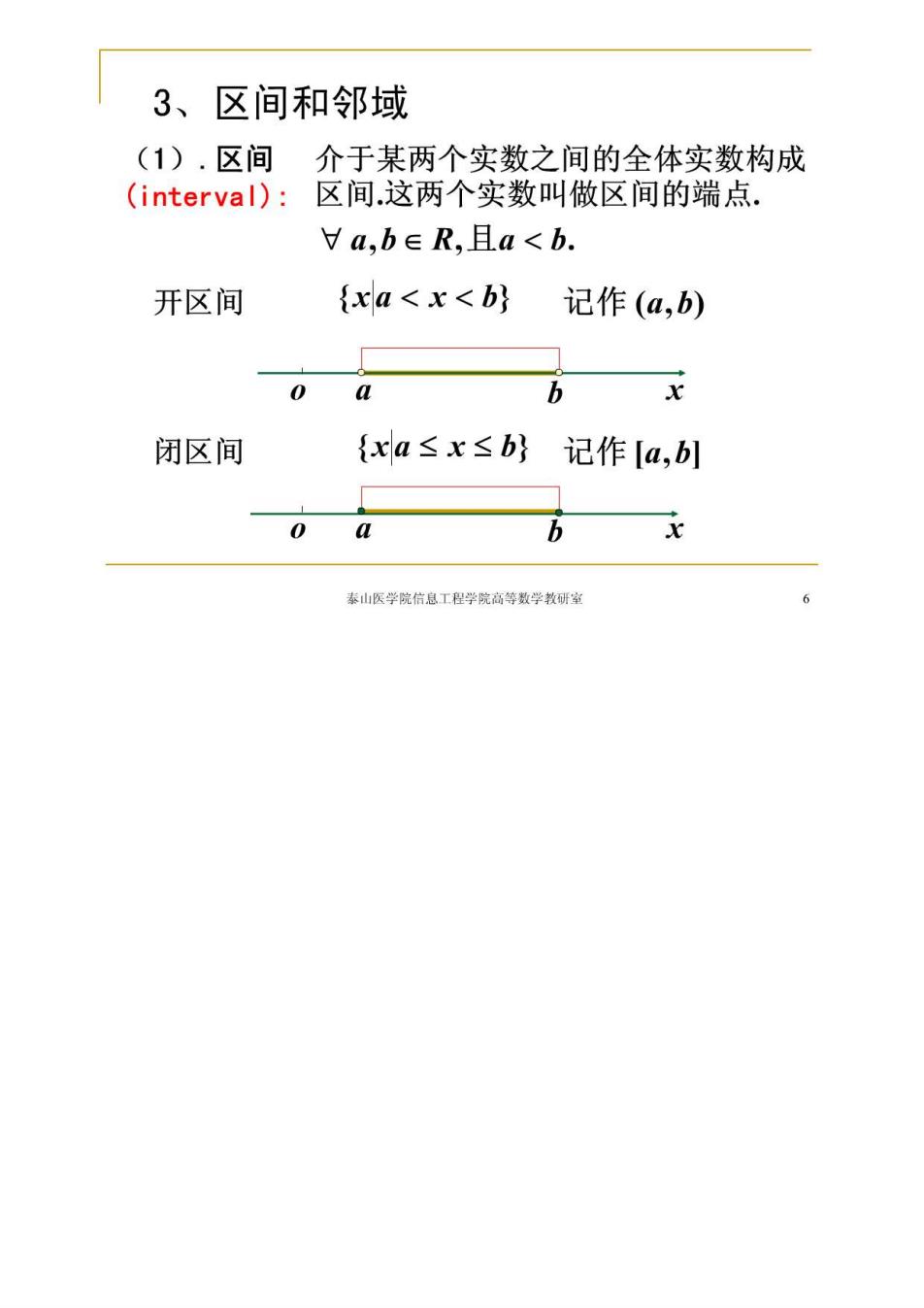
3、区间和邻域 (1).区间介于某两个实数之间的全体实数构成 (interval):区间这两个实数叫做区间的端点. Ya,b∈R,且a<b. 开区间 {xa<x<b 记作(a,b) 0 a 闭区间 {xa≤x≤b}记作[a,b] 0 a 泰山医学院信息工程学院高等数学教研室

左闭右开区间 {xa≤x<b} 记作[a,b) 左开右闭区间 {xa<x≤b} 记作(a,b] 无穷区间【a,+oo)={xa≤x}(-o,b)={xx<b} 0 e 注:两端点间的距离称为区间的长度. 泰山医学院信息工程学院高等数学教研室
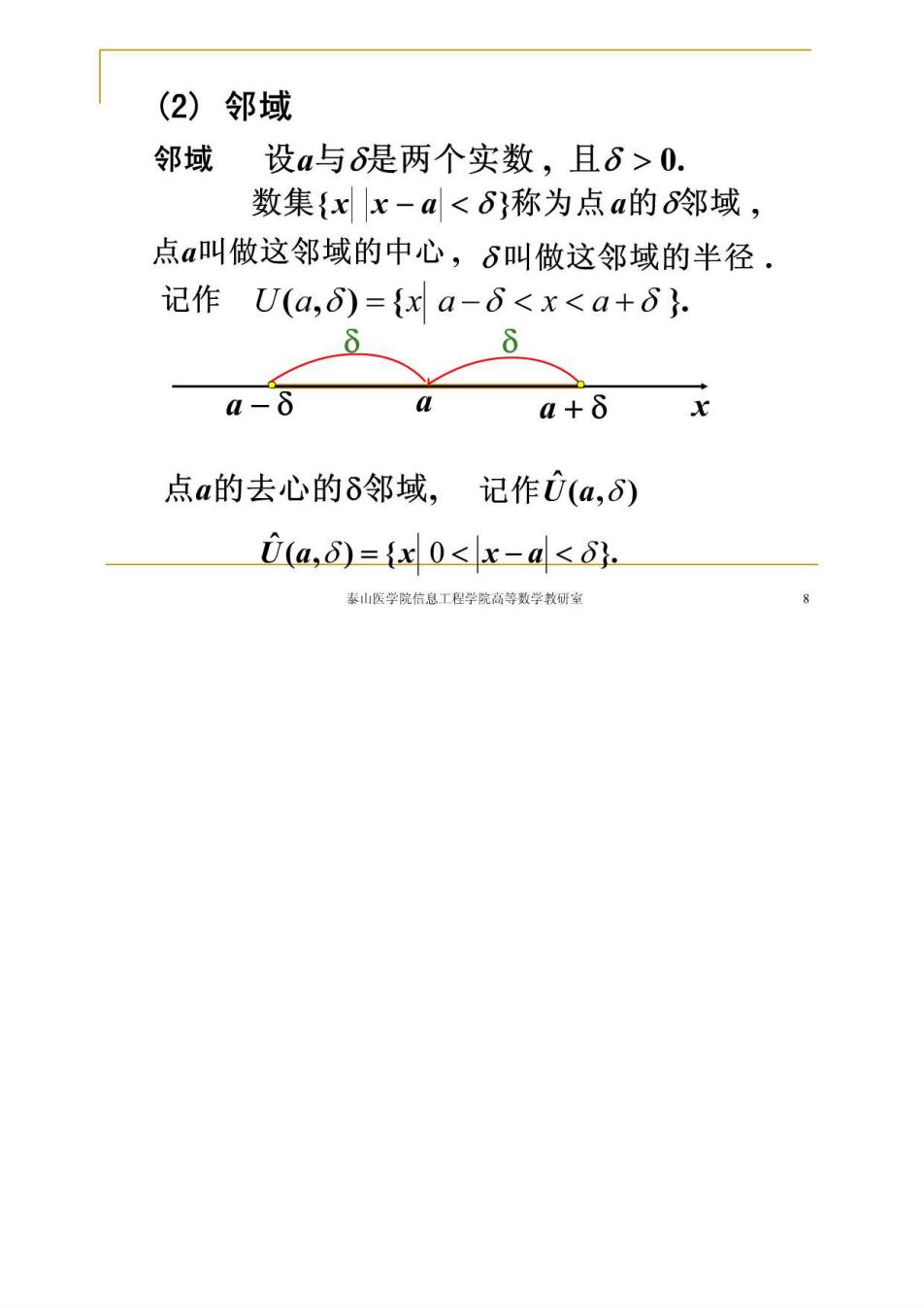
(2)邻域 邻域设a与6是两个实数,且6>0. 数集{xx-a<6}称为点a的邻域, 点a叫做这邻域的中心,6叫做这邻域的半径. 记作U(a,6)={xa-δ<x<a+δ}. a-δ a a+8x 点a的去心的8邻域,记作(a,6) (a,d)={0<x-d<δ. 泰山医学院信息工程学院高等数学教研室

三 映射Mapping) 1映射概念 设X,Y是两个非空集合,如果存在一个法则f, 使得对X中每个元素x,按法则f,在中有唯一的 确定的元素y与之对应,则称为从X到Y的映射, 记作 f:X→Y, 其中y称为元素x的像,并记为f(x),即y=f(x) 而元素x称为元素y的一个原像; 集合X称为映射的定义域,记作D, 集合X中所有元素的像所组成的 集合称为映射的值域,记作R, 泰山医学院信息工程学院高等数学教研室

1)映射的三要素:定义域、对应法则和值域 X 对应法则 Y f(x) 2)对每一个x∈X,元素x的像y是唯一的,而对每 一个y∈R,元素y的原像不一定是唯一的。 例1设f:R→R,对每个x∈R,f(x)=x2. f是一个映射,D,=R,R={U1y≥0} 泰山医学院信息工程学院高等数学教研室