
教案 姓名冯增哲2011~2012学年第二学期 时间 节次 课程名称 高等数学 授课专业及层次 授课内容 定积分元素法利用定积分求平面图形面积学时数 通过教学进一步加深对定积分的理解,提高综合运用知识分析解决问题的能力: 教学目的 掌握定积分元索法和平面图形面积求法 重点 灵活运用知识解题:元素法的概念。平面图形面积求法 难点 利用定积分方法求积分值,灵活运用知识解题 自学内容 《高等数学例题与习题》相关例题,习题 使用教具 多媒体 相关学科知识 无 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾 定积分的概念(为新课的引入作铺垫) 10分钟 2.定积分的各种计算方法 二、进行新课 第六章定积分的应用 第一节定积分的元素法 (一)、以求曲边梯形的面积为例:四个步骤 15分钟 (二)、归纳元素法的一般步骤 元素法的一般步骤 1)根据问题的具体情况,选取一个变量例如X为积分变量,并确定它的 变化区间a,1: 2)设想把区间Ia,b1分成n个小区间,取其中任一小区间并记为x,x+, 求出相应于这小区间的部分量△U的近似值.如果△U能近似地表示为 [a,b1上的一个连续函数在x处的值fx)与d在的乘积,就把rx)称为 量U的元素且记作U,即dU=fx): 3)以所求量U的元素fxk为被积表达式,在区间[a,b1上作定积分,得 U=心f(x)d,即为所求量U的积分表达式. 这个方法通常叫做元素法
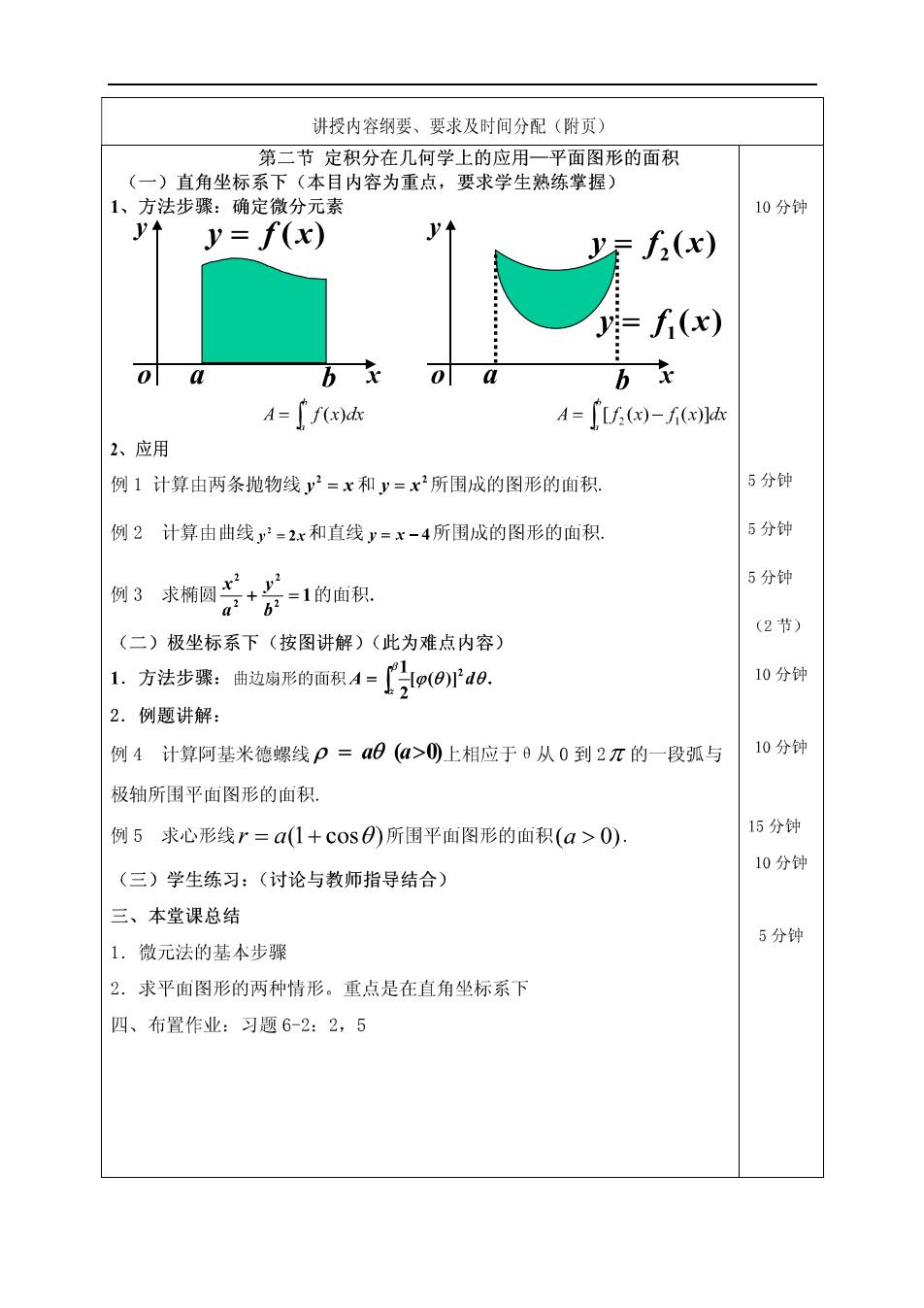
讲授内容纲要、要求及时间分配(附页) 第二节定积分在几何学上的应用一平面图形的面积 (一)直角坐标系下(本目内容为重点,要求学生熟练掌握) 1、方法步骤: 确定微分 10分钟 y=f(x) f(x) Vi= f(x) h b A=∫fx)k A=[L:(x)-f(x)ld 、应用 例1计算由两条地物线y2=x和y=x2所围成的图形的面积 5分钟 例2计算由曲线,y=2x和直线y=x-4所围成的图形的面积. 5分钟 例3求椭同二+-1的自 5分钟 (2节) (二)极坐标系下(按图讲解)(此为难点内容) 1.方法步骤:曲边扇形的面积A=p(0d0. 10分钟 2.例题讲解: 例4计算阿基米德螺线p=a0(a>0)上相应于0从0到2元的一段弧与 10分钟 极轴所围平面图形的面积 例5求心形线r=a(1+cos0)所围平面图形的面积(a>0) 15分钟 10分钟 (三)学生练习:(讨论与教师指导结合) 三、本堂课总结 5分钟 1.微元法的基本步骤 2.求平面图形的两种情形。重点是在直角坐标系下 四、布置作业:习题6-2:2,5

教 案 姓名冯增哲 2011~2012学年第二学期 时间一 节次 课程名称 高等数学 授课专业及层次 授课内容 利用定积分进行体积和曲线弧长的计算 学时数 2 教学目的 会计算旋转体、平行截面已知的立体体积、平面曲线的弧长 重点 体积、平面曲线的弧长计算 难点 对具体问题找出微分元素 自学内容 华东师范大学数学系编《数学分析》相关内容 使用教具 多媒体 相关学科知识 立体几何知识 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 、复习回顾: 5分钟 1.定积分元素法的一般步骤 2.利用定积分求平面图形的面积 二、进行新课: 第六意 定积分的应用 第二节 定积分的几何应用(体积和弧长) (一)求立体体积 1.旋转体体积(本目内容为重点内容,须熟练掌握) (1)定义:旋转体就是由一个平面图形绕这平面内一条直线旋转一周而成的 立体.这直线叫做旋转轴 (2)方法步骤:取一个体积微元,然后积分,最后得旋转体的体积 10分钟 V=「πfxrd (3)例题讲解 例6连接坐标原点O及点P(h,r)的直线、直线x=h及x轴围成一个直 10分钟 角三角形.将它绕x轴旋转构成一个底半径为P、高为h的圆锥体,计算圆 锥体的体积 例7求星形线xi+y5=u(a>0)绕X轴旋转构成旋转体的体积. 10分

讲授内容纲要、要求及时间分配(附页) 例8求摆线x=a1-sin),y=a(1-cos)的一拱与y=0所围成的图形分 15分钟 别绕x轴、y轴旋转构成旋转体的体积. 2、平行截面面积为已知的立体的体积:V=「A(x)d (2节》 例9一平面经过半径为R的圆柱体的底圆中心,并与底面交成角,计算10分钟 这平面截圆柱体所得立体的体积 引导学生分析解题 例10求以半径为R的圆为底、平行且等于底圆直径的线段为顶、高为h的 10分钟 正劈锥体的体积 (二)、平面曲线的弧长 1、参数方程 线溪为0a≤1s点-+-io0+0 10分钟 =√p0+w2G 弧长s=「Vo20+w)d 例1计算摆线x=0-sn0)的一的长度。 Iy=a(1-cos0)' 2.直角坐标方程 8分钟 ds=+ydx 弧长s=V1+y 例12计算曲线y=子x上相应于x从a到b的一段弧的长度, 3.极坐标方程 例13求阿基米德螺线r=a6(a>0)上相应于日从0到2π的弧长 8分钟 三、本堂课总结:体积的求法,重点是旋转体体积:弧长的求法 四、布置作业:习题6-2:11,13,18,22,23

教 案 姓名冯增哲 2011~2012学年第二学期时间节次」 课程名称 高等数学 授课专业及层次 授课内容 定积分在物理上的应用第六章习题课学时数2 教学目的 掌握定积分在物理上的应用通过复习习题学握本章定积分应用 重点 定积分在几何和物理上的应用 难点 微元的确定及积分变量的区间确定 自学内容 华东师范大学数学系编《数学分析》相关内容 使用教具 多媒体 相关学科知识 物理学相关知识 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾: 5分钟 1、微分元素 2、平面面积的计算 3、体积的计算 二、进行新课 第六章定积分的应用 第三节定积分在物理学上的应用 (一人变力沿直线所作的功(引导分析解题) 例1把一个带+9电量的点电荷放在r轴上坐标原点处,它产生一个电场.这个电 10分钟 场对周围的电荷有作用力.由物理学知道,如果一个单位正电荷放在这个电场中距离 原点为”的地方,那么电场对它的作用力的大小为F=k9(k是常数),当这个 单位正电荷在电场中从r=口处沿r轴移动到r=b处时,计算电场力下对它所作 的功 5分钟 例2一圆柱形储水桶为5米,底半径为3米,池内盛满了水问要把池内的水全部吸 出,需作多少功9 (仁)、水压力 例4一个横放者的圆柱形水桶,桶内盛有半桶水,设桶的底半径为R,水10分钟 的比重为y,计算桶的一端面上所受的压力

讲授内容纲要、要求及时间分配(附页) 例5将直角边各为a及2a的直角三角形薄板垂直地浸人水中,斜边朝5分钟 下,直角边的边长与水面平行,且该边到水面的距离恰等于该边的边长,求 薄板所受的侧压力 (三)、引力 例6有一长度为1、线密度为ρ的均匀细棒,在其中垂线上距棒a单位处 有一质量为m的质点M,计算该棒对质点M的引力. 5分钟 学生练习:习题63 5分钟 三、课堂小结: 5分钟 主要要讲述了平面曲线求长度,以及变力所作的功、压力、引力的计算 (2节)》 四、第六章复习:(一)主要内容回顾 定积分的元素法 10分钟 求平面图形的面积 定积分的应用定积分在几何上的应用 求体积 求平面曲线的弧长 「功的问题 定积分在物理上的应用 水压力问题 引力问题 (二)、例题精讲 1 例1一金属棒长3m,离棒左端m处的线南度为()市您/m),问x为何10分钟 值时,[0,x一段的质量为全棒质最的一半。 例2设抛物线y=ax2+bx+c通过点(0,0),月当x∈[0,]时,y≥0,试确定 10分钟 a,b,c的值,使得抛物线y=2+br+c与直线x=1,y=0所围成的图形面积为 4 0 月使该图形绕x轴旋转而成的转体的体积最小 例3求圆盘(化-2)+y2≤1绕y轴旋转而成的旋转体的体积。 10分钟 学生课常练习:总习题六(P2882,4,6) 5分钟 五、本堂课总结,布置作业:习题6-32、9、11 5分钟