
教案 姓名刘桂姐 2011~2012学年第二学期时间9.19节次1-23-4 课程名称 高等数学 授课专业及层次2011级电子信息本、计算机本 授课内容 映射与函数 学时数 2 复习集合、映射的有关概念:理解函数的概念,了解函数的奇偶性、单调性、周 教学目的 期性、有界性。 重点 陕射、函数的概念 难点 逆映射、复合映射的概念 自学内容 集合、函数的奇偶性、单调性 使用教具 多媒体 相关学科知识 初等数学知识 教学法 讲解、谈话 讲授内容纲要、要求及时间分配 引言: 1.师生交流:(1)教师自我介绍 (2)谈话 20分钟 2 高等数学的内容概括 3.学习高等数学的意义 (1)基础性(2)应用性(3)名人学数学 4.怎样学好高等数学?(1)加强对概念的理解和体会(2)深钻教科书 (3)精做习题,灵活应用 5。与初等数学的比较(1)考察问题的观念:变化的观念(2)研究的对象:函数 (3)研究的方法:极限方法 6.参考书及考核方式 二、讲授新课: 第一章函数与极限 第一节映射与函数 10分钟 (一)集合(自学为主,注意与初等数学的衔接) 1、集合概念 2、集合的表示方法:列举法,描述法 3、集合的运算:(学生课下自学) 讲解.差集:AB=钟∈AHxeB时直积:AxB=《化,水∈Ay∈B 4、区问和邻域 详细讲解邻域的概念:点a的5邻域,U(a,d) 点a的去心8邻域U(a,d) (二)映射 1、映射概念(简单介绍)

讲授内容纲要、要求及时间分配(附页) 定义设X,Y是两个非空集合,如果存在一个法则f,使得对X中的每一个元素x 按法则f,在Y中有唯 一确定的元素)与之对应,则称为从X到的缺射,记作 :X 其中y称为元素x的像,并记作),即y=f) 10分钟 注意:1)集合X:集合Y:对应法则f 2)每个X有唯一的像:每个Y的原像不唯一 2、儿种重要的映射:满射,单射,一一映射 10分钟 3、逆肤射与复合映射 (简单介绍,采用启发式教学) (三)函数(重点讲解) 1、讲解函数的概念:(1)函数的定义:设数集DcR,则称映射f:D→R为定义 15分钟 在D上的函数 记为y=f(x)x∈D 自变量、因变量、定义域、值域、函数值 (2)确定函数的两个要素:定义域及对应关系 (3)单值函新、多值函斯 10分钟 (4)几种特殊函数:符号函数,取整函数、分段函数(逐个举例,间图讲解) 2、函数的几种特性(重点介绍有界性) 10分钟 (1)有界性:f(x)在X上有上界、下界:有界,无界 (2)单调性(学生课下自学) (3)奇偶性(学生课下自学 (1)周期性:举例教材例10 5分钟 失利克玉西数00-日堂。任制省程数电是的阀期它发省银木用 期。 7分钟 三、学生习作:习题1-11、2,7 四、课堂总结:加强对映射、函数概念的理解。 3分钟 布置作业:习题1-14.(6)(7)(8)(9)5.(1)(3)6
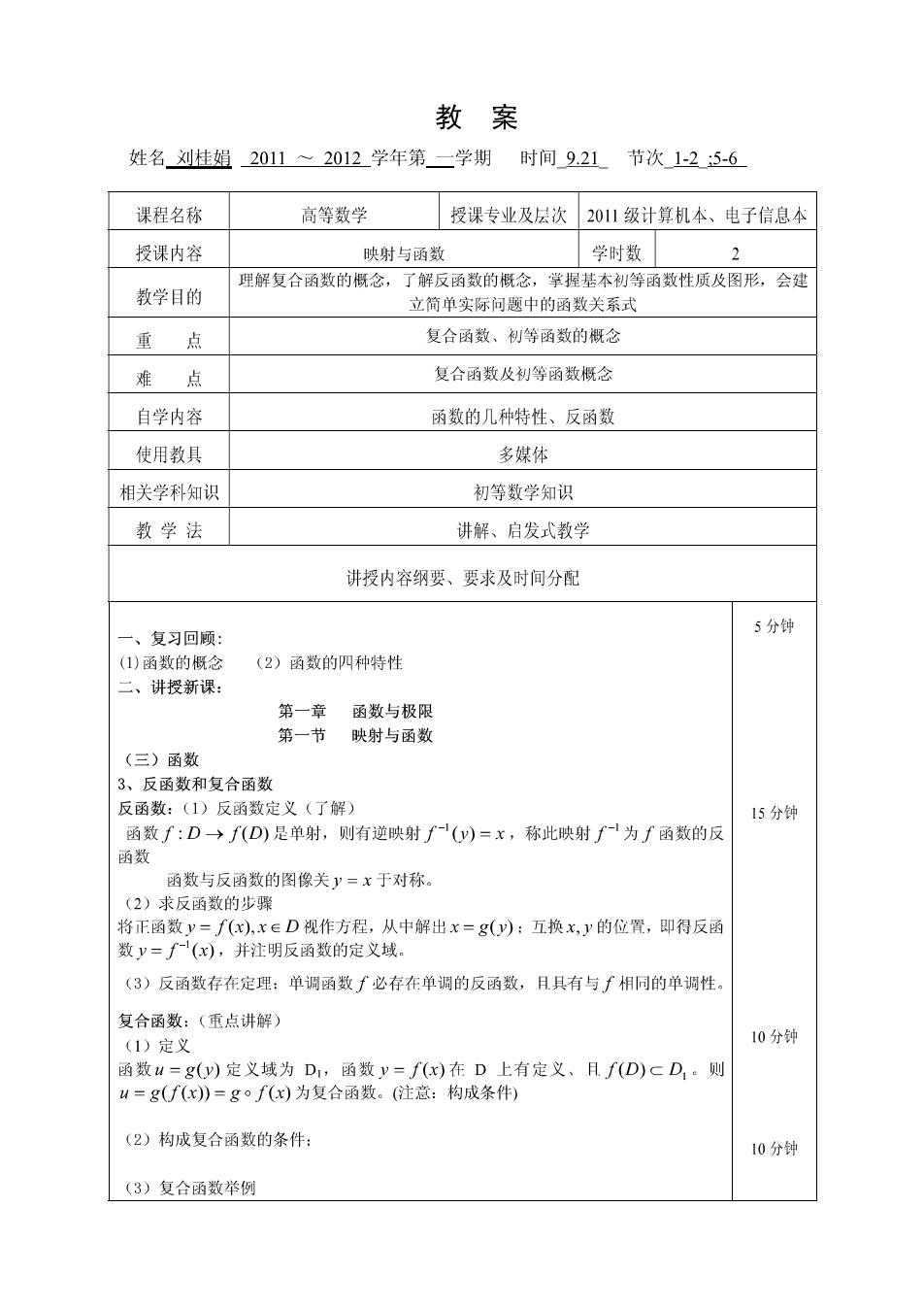
教案 姓名刘桂姐2011~2012学年第二学期时间9.21节次1-2:5-6 课程名称 高等数学 授课专业及层次2011级计算机本、电子信息本 授课内容 映射与函数 学时数 2 理解复合函数的概念,了解反函数的概念,掌握基本初等函数性质及图形,会建 教学目的 立简单实际问题中的函数关系式 重点 复合函数、初等函数的概念 难点 复合函数及制等函数概念 自学内容 函数的几种特性、反函数 使用教具 多媒体 相关学科知识 初等数学知识 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 、复习回顾」 5分钟 ()函数的概 (2)函数的四种特性 二、讲授新课: 第一章函数与极限 第一节映射与函数 (三)函数 3、反函数和复合函数 反函数:(1)反函数定义(了解) 15分钟 函数f:D→f(D)是单射,则有逆映射f-(y)=x,称此映射f-为f函数的反 函数 函数与反函数的图像关y=x于对称 (2)求反函数的北骤 将下函数y=f()x∈D视作方程,从中解出x=g):五换x,y的位置,即得反 数y=(,并注明反函数的定义域。 (3)反函数存在定理:单调函数∫必存在单调的反函数,月具有与∫相同的单调性 复合函数:(重点讲解) (1)定义 10分钟 函数u=g(y)定义域为D,函数y=f()在D上有定义、Rf(D)CD,。则 =g》=g0了为复合函数。(注意:枸成条制 2)构成复合函数的条件: 10分钟 (3)复合函数举例

讲授内容纲要、要求及时间分配(附页) 4、函数的运算 10分钟 两个函数的和、差、积、商:(板书讲解 分r教材例11 5、初等函数 基本初等函数:幂函数、指数函数、对数函数、二角函数、反二角函数 (要求熟悉定义域、值域、性质、图形) 1)幂函数:y=x” 10分钟 4)二角函数 y=sin(x),y=cos(x),y=tan(x),y =cot(x) 5)反二角函数(因中学没学,需详细讲解) 15分钟 y=arcsin(x).v=arccos(x) y=arctan(x) y=arccot(x) 初等函数 10分钟 (1)讲解制等函数的定义。 (2)初等函数举例 三、学生习作:习题1-1、12、14 10分钟 四、课堂总结:加强对函数、复合函数,初等函数的理解,熟练掌握复合函数的分解 5分钟 布置作业:习题1-115.(2)(4)16.17
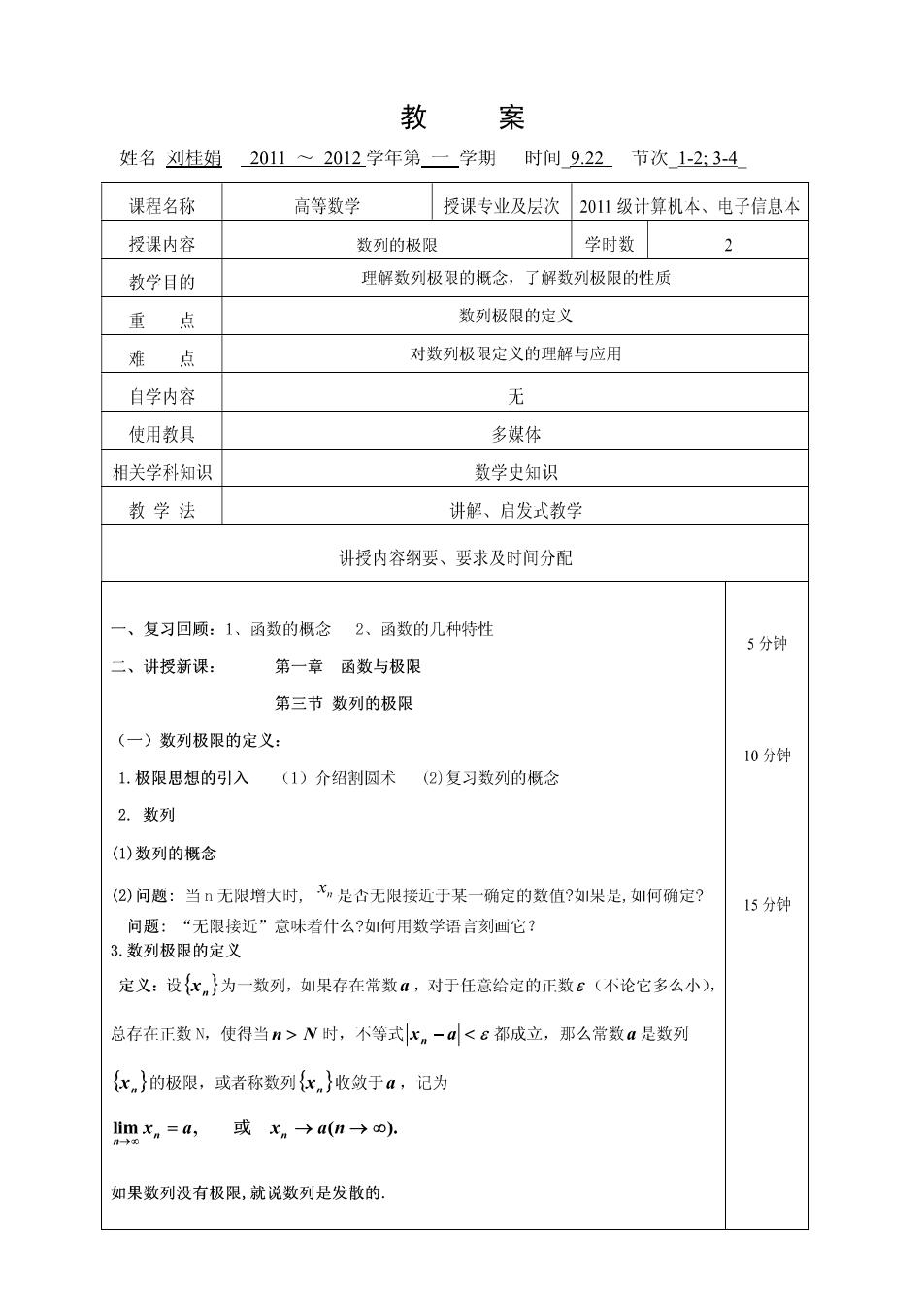
教 案 姓名刘桂姐2011~2012学年第一学期时间9.22节次1-2:3-4 课程名称 高等数学 授课专业及层次201级计算机本、电子信息本 授课内容 数列的极限 学时数 2 教学目的 理解数列极限的概念,了解数列极限的性质 重点 数列极限的定义 难点 对数列极限定义的理解与应用 自学内容 无 使用教具 多媒体 相关学科知识 数学史知识 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾:1、函数的概念2、函数的几种特性 5分钟 二、讲授新课: 第一章函数与极限 第三节数列的极限 (一)数列极限的定义: 10分钟 1.极限思想的引入(1)介绍割圆术(2)复习数列的概念 2.数列 (1)数列的概念 (②)问题:当无限增大时,X是杏无限接近于某一确定的数值?如果是,如何确定? 15分钟 问题:“无限接近”意味者什么?如何用数学语言刻画它? 3.数列极限的定义 定义:设{化}为一数列,如果存在常数a,对于任意给定的正数6(不论它多么小), 总存在正数N,使得当n>N时,不等式k。-<c都成立,那么常数a是数列 {xn}的极限,或者称数列{xn}收纹于a,记为 imx.=a,或x。→a→o)h 如果数列没有极限,就说数列是发散的

注意:1,不等式。-d小0成立寻找、但木必要求最小 的N 学生练习:习题1-21、 学生讨论:习题1-23、(1)(2) (仁)、收敛数列的性质 定理1(极限的唯一性)如果数列{化}收效,那么它的极限唯一。 15分钟 引导分析并证明 讲解教材例愿4 数列{x}有界的定义 定理2(收敛数列的有界性)如果数列化。}收敛,那么数列化}一定有界。 15分钟 引导分析并证明。 定理3(收敛数列的保号性)如果imx,=a,a>0(aN时,都有x>0 引导分析并证明, 定理4(收敛数列与其子数列的关系)如果数列{化}收敛于,那么它的任一子数 5分钟 列也收敛,月极限也是a。 引导分析并证明。 三、学生习作,教师答疑 5分钟 四、课堂总结:加强对数列极限定义的理解,熟悉性质的条件与结论 布置作业:P0习题1-2 1、(2)(4)(6)(8)3.(2)(3
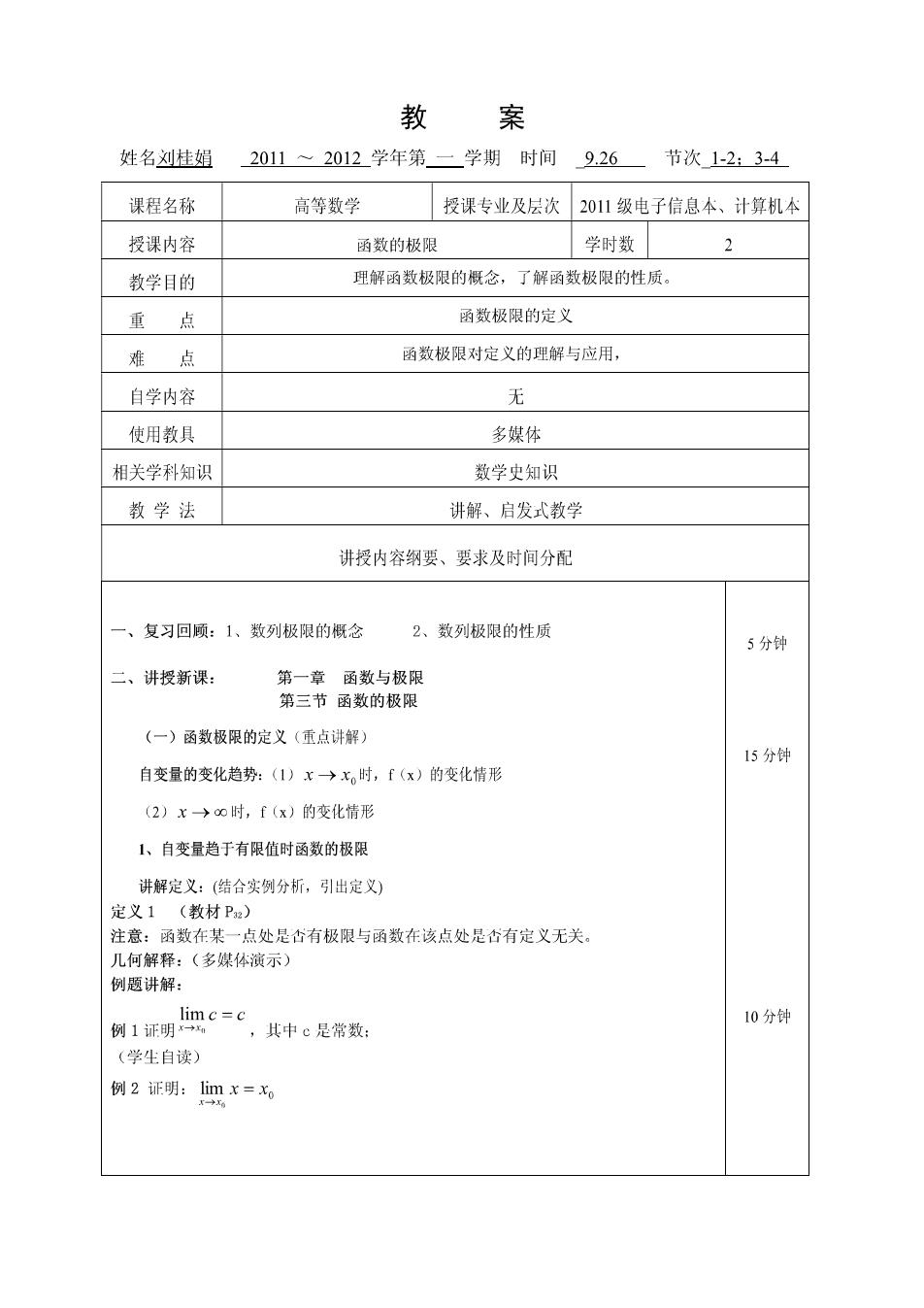
教 案 姓名刘桂姐 2011~2012学年第一学期时间9.26节次1-2:3-4 课程名称 高等数学 授课专业及层次2011级电子信息本、计算机本 授课内容 函数的极限 学时数 2 教学目的 理解函数极限的概念,了解函数极限的性质。 重点 函数极限的定义 难点 函数极限对定义的理解与应用, 自学内容 无 使用教具 多媒体 相关学科知识 数学史知识 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾:1、数列极限的概念 2、数列极限的性质 5分钟 二、讲授新课: 第一章函数与极限 第三节函数的极限 (一)函数极限的定义(重点讲解) 15分钟 自变量的变化趋势:(1)x→x。时,「(x)的变化情形 (2)x→o时,f(x)的变化情形 【、自变量趋于有限值时函数的极限 讲解定义:(结合实例分析,引出定义) 定义1(教材P) 注意:函数在某一点处是古有极限与函数在该点处是古有定义无关。 ,其中c是常数: 10分钟 (学生自读) 例2证明:Iinx=

例3、求函数的极限 10分钟 im(2x-1)=3 (引导学生分析并解题) 函数在有限点0处的左右极限 5分钟 函数皿代⊙存在的充分必要条是)在处的左、右极限都存在并且相等,即 f(xo)=f(xo) 结论 一个在点的士心邻线有定义函数,如果()与)都存在,但不 相等,或者。)与中全少有一个不存布,则/)在点处无极限 5分钟 1 x>0 函数:fx)=sgnx 0 X=0 例4、证明: -1x<0当x→0时极限不存在。 15分钟 2、函数在无穷大处的极限 (1)、x→D时的极限 (2)、x→o0时的极限 (3)、x→-0时的极限 结论.血)存在的充分必要条件是血)与m)都存在并且相等 学生练习:习题1-31、 15分钟 (二)函数极限的性质 定理1(极限的唯一性) 定理2(极限的局部有界性) 15分钟 定理3(极限的局部保号性 定理4(极限与数列极限的关系) (引导启发教学给出定理2、定理3、定理1的证明) 三、学生习作,教师答疑 5分钟 四、课堂总结:加强对函数极限的理解,熟悉函数的性质 布置作业:P习题1-31,2

教 案 姓名刘挂姐2011~2012学年第一学期时间9.28节次1-2:5-6 课程名称 高等数学 授课专业及层次2011级计算机本、电子信息本 授课内容 无穷小与无穷大 学时数 2 教学目的 理解无穷小、无穷大的概念:掌握无穷小量的性质。 重点 无穷小、无穷大的概念:无穷小量的性质 难点 无穷小量的性质的理解 自学内容 无 使用教具 多媒体 相关学科知识 无 教学法 讲解、启发式教学 讲授内容纲要、要求及时间分配 一、复习回顾: 5分钟 1、数列极限的概念2、函数极限的定义3、函数极限的性质 二、讲授新课: 函数与极限 无穷小与无穷大 (一无穷小与无穷大 10分钟 1、无穷小定义 2、举例:例1 注意:无穷小是一个极限为零的函数,除了常数零可作无穷小外,其他任何非零常数, 即使绝对值很小,都不是无穷小。 3、定理1:在自变量的同一变化过程中,(x)具有极限A的充要条件是 f (x) -A+ 其中a是无穷小。 引导学生分析并证明: (二)无穷大定义 10分钟 1、无穷大的定义:(教材P) 注意:(1)无穷大不是一个数,而是函数的极限 (2)无穷大与无界量不同 讲解例2

讲授内容纲要、要求及时间分配(附页) 铅直渐近线: 如果mf)=,则直线x=是函数v=f代刊的图形的铅直新近线。 15分钟 2、无穷小与无穷大的关系 2)若是无穷小R闭:0,侧网是无穷大 1 10分钟 引导学生分析并证明: 10分钟 学生练习:习题1-45、 第五节极限的运算法则 讲解:无穷小的性质: 定理1:有限个无穷小之和是无穷小 10分钟 引导分析证明 定理2:有界函数与无穷小之积是无穷小 引导分析证明 10分钟 推论(1):常数与无穷小之积是无穷小:(2):有限个无穷小之积是无穷小 司求极程回m》 15分钟 三、学生习作,教师答疑 5分钟 四、课堂总结:理解无穷小、无穷大的概念:掌握无穷小量的性质。 布置作业:习题1-12.(1)1.8