
高等数学最重要的概念是什 么,相当一部分同志对这个问题 看法是:高等数学这个课程最重 要、最基本的概念是极限,我不 是太赞成这个看法,你要说高等 数学,那首先是微分、积分这些 概念弄清楚,并且会用,我觉得 高等数学的重点首先应该是这 个。 一著名数学家北京大学教授姜伯驹院士 2012329 泰山医学院信息工程学院高等数学教研家

第二章 导数与微分 微分学是微积分的重要组成部分,它的 基本概念是导数与微分,其中导数反映出 函数相对于自变量变化的快慢程度,而微 分则指明当自变量有微小变化时,函数大 体上变化多少。 在这一章中,主要讨论导数和微分的 概念以及它们的计算方法,关于导数的 应用,将在第三章讨论。 2012-3-29 泰山医学院信息工程学院高等数学教研室 2

第一节 导数概念 (The Derivative) 一问题的提出 二 导数的定义 三四五 由定义求导数举例 导数的意义 五可导与连续的关系 六小结与思考判断题 2012-3-29 泰山医学院信息工程学院高等数学教研室 3

重点:导数的定义及几何意义 难点:用定义求导数 关键:抓住用定义求导数的三个步骤 2012329 泰山医学院信息工程学院高等数学教研室

问题的提出Introduction) 1.直线运动的速度问题 如图,设动点于时刻在直线上的位置的坐标为s, 即位置函数为s=f(),求t时刻的瞬时速度· 取一邻近于t的时刻t,运动时间△t, 平均速度下=4s=-=f0-f) At t-to t-to 瞬时速度v=im0-f化)、名, 当t→t时,取极限得 1→%t-to 2012329 素山医学院信息工程学院高等数学教研室
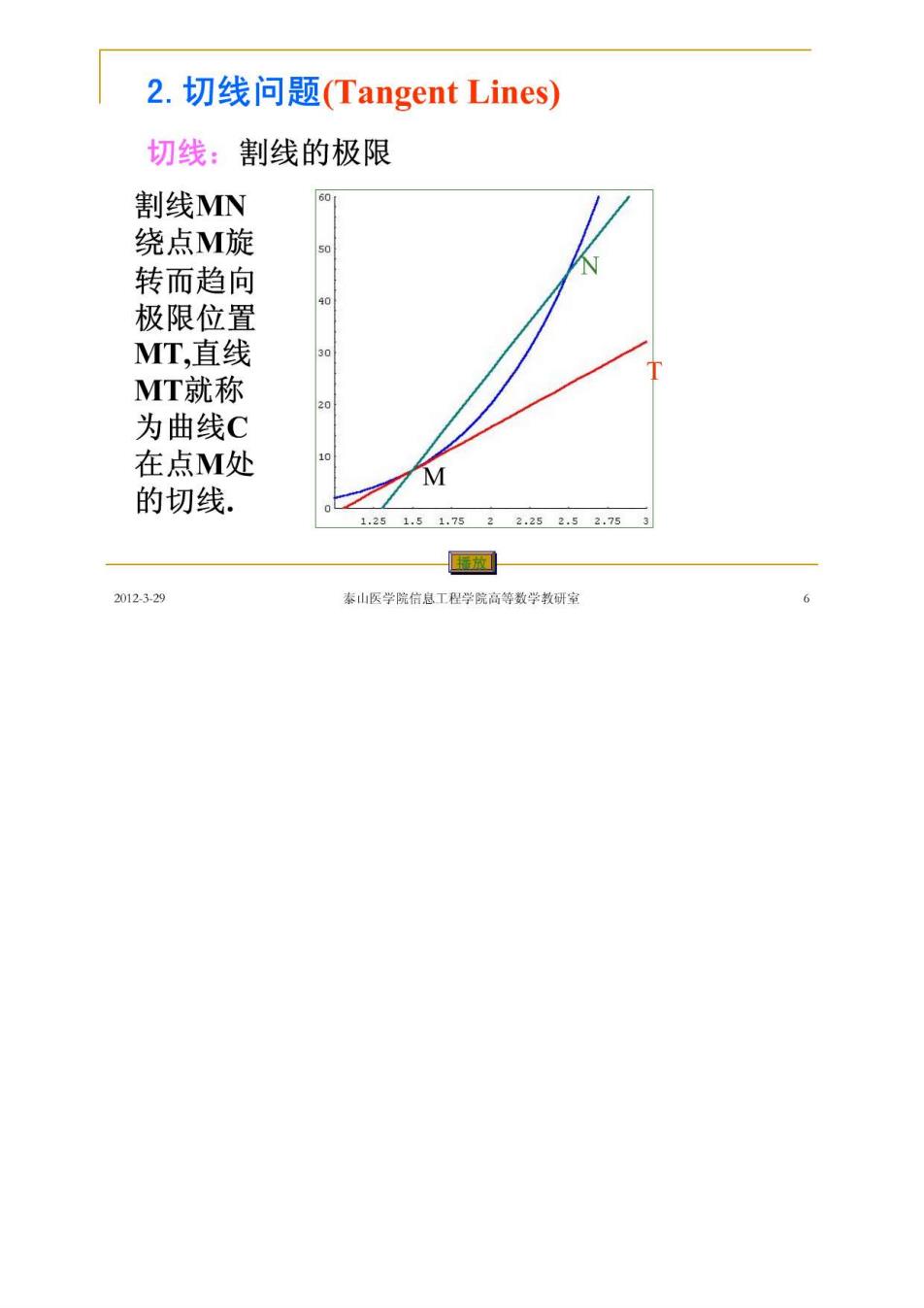
2.切线问题(Tangent Lines) 切线:割线的极限 割线MN 绕点M旋 转而趋向 极限位置 MT,直线 MT就称 为曲线C 在点M处 M 的切线. 1.251.51.7522252.52753 网 2012329 泰山医学院信息工程学院高等数学教研家

设M(xo,yo),N(x,y). y=f(x)入 割线MN的斜率为 2 C M tano=-o x-xo -(x)-) Xo x-x。 N沿曲线CM,x→x0, 切线MT的斜率为k=tana=lim f(x)-f(xo) x→x0X-X0 2012329 泰山医学院行息工程学院高等数学教研室

二导数的定义 (Definition of Derivatives) 1.定义设函数y=f(x)在点x的某个邻域内 有定义,当自变量x在x处取得增量△x(点 x,+△x仍在该邻域内)时,相应地函数y取 得增量△y=f(x,+△x)-f(x);如果△y与 △x之比当△x→0时的极限存在,则称函数 y=f(x)在点x处可导,并称这个极限为函 数y=f(x)在点x处的导数,记为yx=, 的1 在f'(x) 2012329 素山医学院信息工程学院高等数学教研室

即y=l △y=im (x。+△x)-f(x) Ar→0△XAr→0 △x 导数定义其它常见形式: f(xo)=lim f(x)-f(xo) r→xa x-xo f(x)=lim(-f(x.) h 2012329 素山医学院信息工程学院高等数学教研室

注1) △y表示因变量在以x,和x,+△x 为端点的区间上的平均变化率 2)f'(x)是因变量在点x处的变化率,它 反映了因变量随自变量的变化而变化的快 慢程度. 3)如果四是不存在,则称=心在不可导。 若1imAy=o,称y=f(在x,处的导数为无穷大. Ar→0△r 2012329 泰山医学院信息工程学院高等数学教研室 10