
第一节多元函数的基本概念 一、平面点集 二、多元函数概念 三、多元函数的极限 四、多元函数的连续性 2012-3-29 泰山医学院信息工程学院高等数学教研室 1

平面,点集 邻域 回忆 .o 设a与6是两个实数,且6>0. 数集{xx-a<6称为点a的6邻域记作U(a,6) U(a,6)={xx-al<6} 点a叫做这邻域的中心,6叫做这邻域的半径 U(a,6)={xa-6<x<a+6} a-u a+δ 2012329 泰山医学院信息工程学院高等数学教研室

1.邻域 点集U(P,)={PPP<6},称为点P的6邻域. 例如,在平面上, P。 U(B,8)={x,y)V(x-xo)2+y-o)2<6}6 (圆邻域) 在空间中, U(B,6)={(x,y,zVx-x)2+0y-)2+(z-zo)2<6} (球邻域) 说明:若不需要强调邻域半径δ,也可写成U() 点P。的去心邻域记为P)={P叶0<P<} 2012.329 奉山医学院信息工程学院高等数学教研室

2.区域 (①)内点、外点、边界点 设有点集E及一点P: ·若存在,点P的某邻域U(P)cE, 则称P为E的内点; ·若存在,点P的某邻域U(P)∩E=② 则称P为E的外点; 。若对点P的任一邻域U(P)既含E中的内,点也含E 的外点,则称P为E的边界点· 显然,E的内点必属于E,E的外点必不属于E,E的 边界点可能属于E,也可能不属于E 2012329 泰山医学院信息工程学院高等数学教研室

(②)聚点 若对任意给定的δ,点P的去心 邻域U(P,)内总有E中的点,则 称P是E的聚,点。 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界点) 例如:设平面点集 E={(x,y1<x2+y2≤2}. 满足1<x2+y2<2的一切,点(化,y)都是E的内点; 满足x2+2=1的一切点(x,y)都是E的边界,点,它们都不属于E; 满足x2+2=2的一切点(心,y)也是E的边界点,它们都属于E: 点集E以及它的界边E上的极点都是E的聚,点. 5

(③)开区域及闭区域 ·若点集E的点都是内点,则称E为开集; ·E的边界,点的全体称为E的边界,记作E; ·若点集EoOE,则称E为闭集; ·若集D中任意两点都可用一完全属于D的折线相连, 则称D是连通的; ·连通的开集称为开区域,简称区域; 。开区域连同它的边界一起称为闭区域。 2012329 泰山医学院信息工程学院高等数学教研室
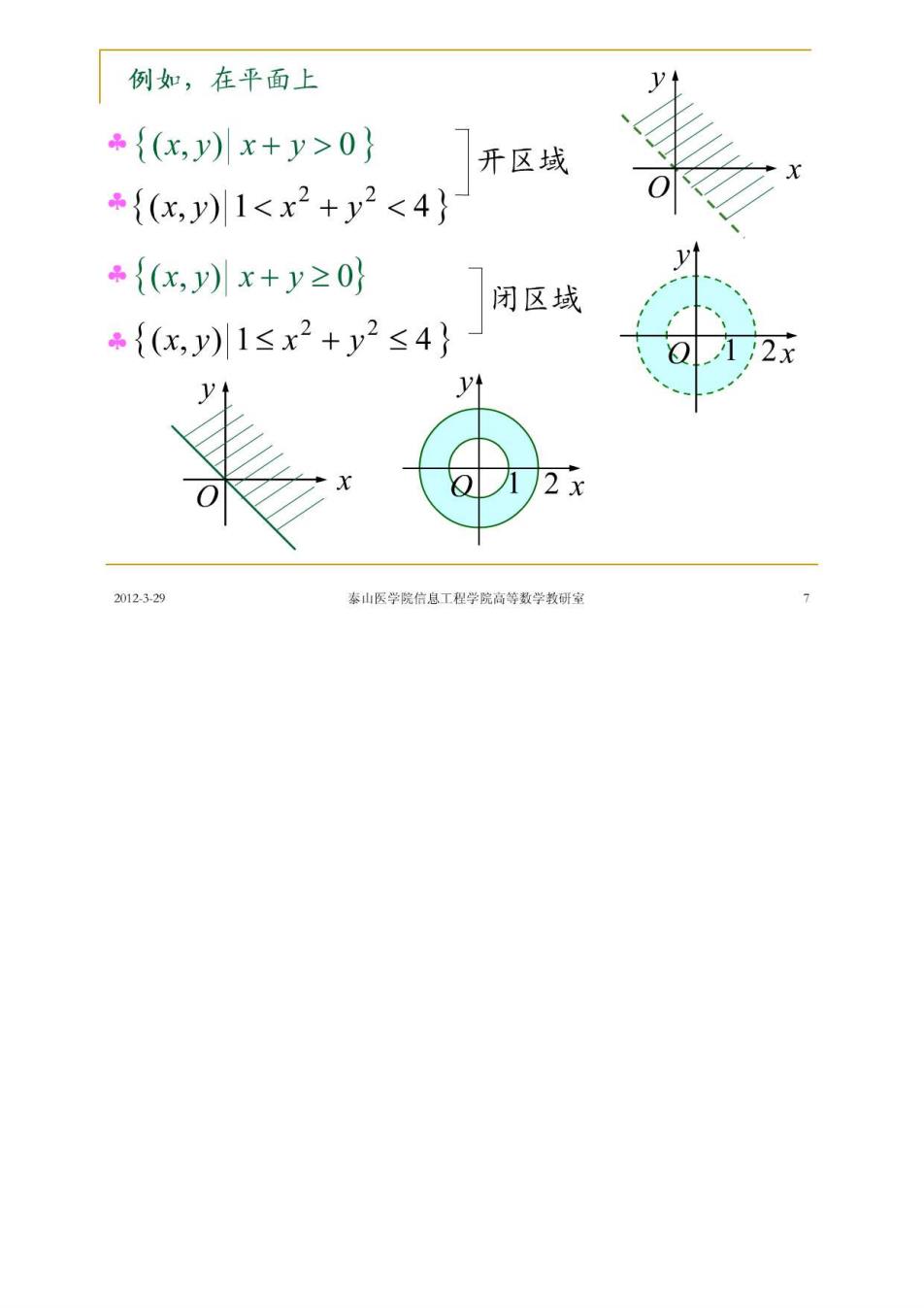
例如,在平面上 {(x,y)x+y>0} 开区域 *{(x,y)1<x2+y2<4} {(x,y)川x+y≥0} 闭区域 *{(x,y)1≤x2+y2≤4} 2012.329 泰山医学院信息工程学院高等数学教研蜜

整个平面是最大的开域, 也是最大的闭域; +点集{(x,y)x>}是开集, 但非区域 ·对区域D,若存在正数K,使一切点PD与某定点 A的距离APkK,则称D为有界域,否则称为无界域. 举例: 点集{x,y1≤r2+y2≤4}是有界闭区域; E 点集{,川x+y>1}是无界开区域: 点集{x,y川x+21}是无界闭区域. 2012329 泰山医学院信息工程学院高等数学教研室

(4)n维空间 实数x←一一对应数轴,点 实数全体表示直线(一维空间)R 数组化,)一应平面点 (化,)全体表示平面(二维空间)R 数组化,八,习一一对应空间点 化,以,)全体表示空间(三维空间)R3 推广:n维数组(,x 全体称为m维空间,记为R”. 2012329 泰山医学院信息工程学院高等数学教研蜜

n维空间中两点间距离公式 设两点为P(1,x2,.,xn为(1,y2,.》n |P1=V(y-x)2+(y2-x2)2+.+(yn-xn)2. 特殊地,当n=1,2,3时,便为数轴、平面、空间两 点间的距离. n维空间中邻域概念: U(E,δ)={PPRK6,P∈R"} 区域、内点、边界点、区域、聚点等概念也可定义,一 2012329 泰山医学院信息工程学院高等数学教研室