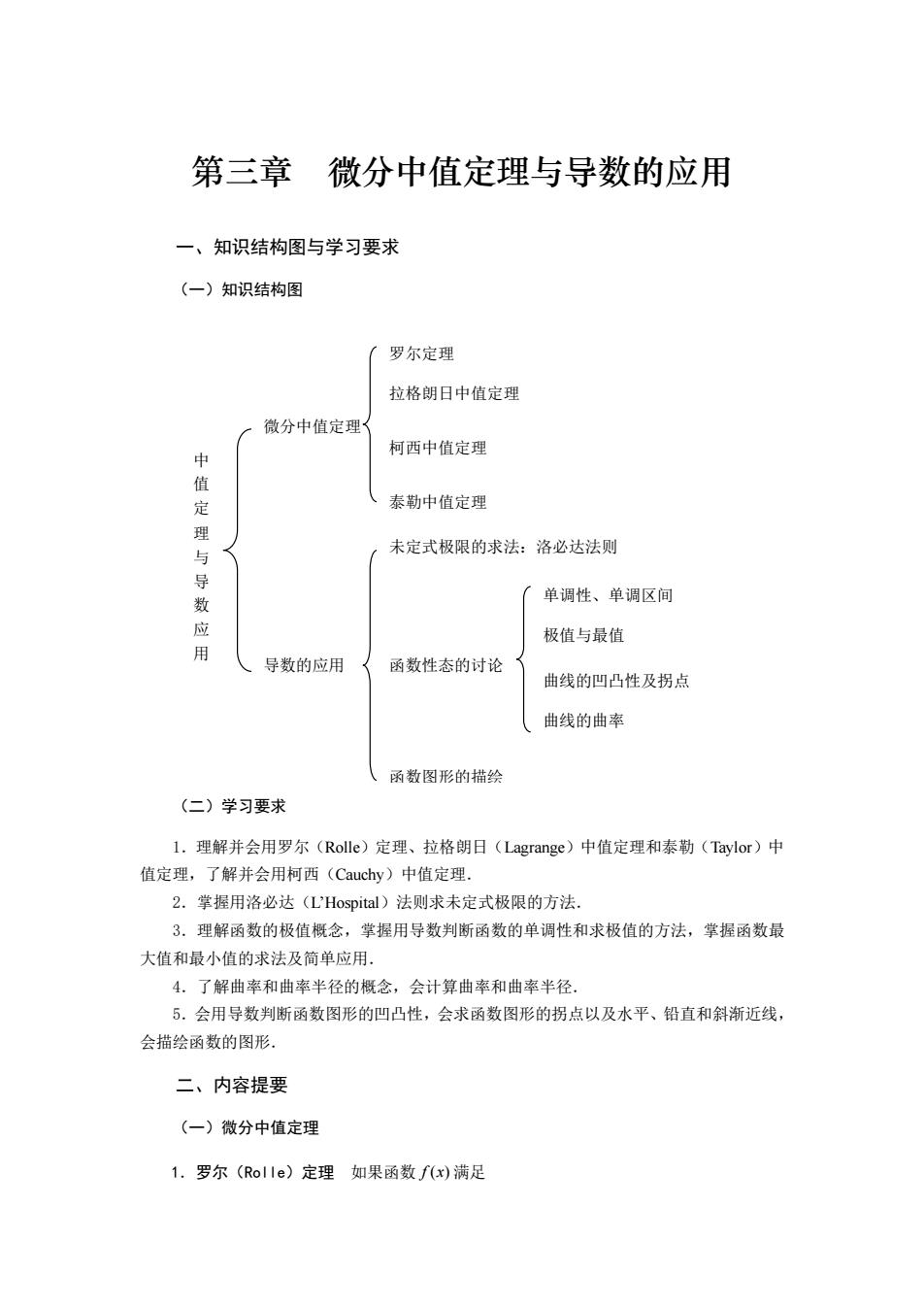
第三章微分中值定理与导数的应用 一、知识结构图与学习要求 (一)知识结构图 罗尔定理 拉格朗日中值定理 微分中值定理1 柯西中值定理 值 、泰勒中值定理 与 未定式极限的求法:洛必达法则 导数 单调性、单调区间 极值与最值 导数的应用 函数性态的讨论 曲线的凹凸性及拐点 曲线的曲率 、函数图形的描绘 (二)学习要求 L.理解并会用罗尔(Role)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)中 值定理,了解并会用柯西(Cauchy)中值定理. 2.掌握用洛必达(LHospital)法则求未定式极限的方法。 3.理解函数的极值概念,掌握用导数判断函数的单调性和求极值的方法,掌握函数最 大值和最小值的求法及简单应用。 4.了解曲率和曲率半径的概念,会计算曲率和曲率半径。 5。会用导数判断函数图形的凹凸性,会求函数图形的拐点以及水平、铅直和斜渐近线, 会描绘函数的图形. 二、内容提要 (一)微分中值定理 1.罗尔(Rolle)定理如果函数fx)满足
第三章 微分中值定理与导数的应用 一、知识结构图与学习要求 (一)知识结构图 (二)学习要求 1.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)中 值定理,了解并会用柯西(Cauchy)中值定理. 2.掌握用洛必达(L’Hospital)法则求未定式极限的方法. 3.理解函数的极值概念,掌握用导数判断函数的单调性和求极值的方法,掌握函数最 大值和最小值的求法及简单应用. 4.了解曲率和曲率半径的概念,会计算曲率和曲率半径. 5.会用导数判断函数图形的凹凸性,会求函数图形的拐点以及水平、铅直和斜渐近线, 会描绘函数的图形. 二、内容提要 (一)微分中值定理 1.罗尔(Rolle)定理 如果函数 f x( ) 满足 中 值 定 理 与 导 数 应 用 函数性态的讨论 拉格朗日中值定理 微分中值定理 导数的应用 罗尔定理 泰勒中值定理 柯西中值定理 单调性、单调区间 极值与最值 未定式极限的求法:洛必达法则 曲线的凹凸性及拐点 曲线的曲率 函数图形的描绘

(1)在闭区间a.b1上连续: (2)在开区间(a,b)内可导: (3)在区间端点处的函数值相等,即fa=fb) 那么在(a,b)内至少有一点5(a<5<b),使得f(⑤)=0. 2.拉格朗日(Lagrange)中值定理如果函数fx)满足 (1)在闭区间[a,b)上连续: (2)在开区间(a,b)内可导 那么在(a,b)内至少有一点(a<5<b),使等式 f(b)-f(a)=f(5Xb-a) 成立 拉格朗日中值定理的其它形式: fb-fa=f'(a+b-a)b-a,0<0<1: f)=)+∫(5x-),专在x与x之间: fx)=f)+f'(x+x-xx-),0<0<1: fx。+)=f()+f"(E)h,5在与+h之间. 3.柯西(Cauchy)中值定理如果函数fx)及F(x)满足 (1)在闭区间[a,b1上连续: (2)在开区间(a,b)内可导: (3)对任一x∈(a,b),F(x)≠0, 那么在(a,b)内至少有一点5(a<5<b),使等式 成立 注1中值定理中罗尔定理可以认为是最基本的,因为其它两个中值定理均能用它导 出,而拉格朗日中值定理是最常用的: 注2罗尔定理、拉格朗日中值定理和柯西中值定理的条件都是充分条件但不是必要条 件. 4.泰勒(Taylor)公式 (1)泰勒(Taylor)中值定理如果函数f(x)在含有,的某个开区间(a,b)内具有直 到(n+1)阶的导数,则对任一x∈(a,b),有 国-=c+f-0+/a-+-xy+R国. 其中风国=识:-产(5是在气与之间的果个值,格风为啦格嗣日型余现 注上面四个中值定理之间的关系图
(1)在闭区间 [ , ] a b 上连续; (2)在开区间 ( , ) a b 内可导; (3)在区间端点处的函数值相等,即 f a f b ( ) ( ) = , 那么在 ( , ) a b 内至少有一点 ( ) a b ,使得 f ( ) 0 = . 2.拉格朗日(Lagrange)中值定理 如果函数 f x( ) 满足 (1)在闭区间 [ , ] a b 上连续; (2)在开区间 ( , ) a b 内可导, 那么在 ( , ) a b 内至少有一点 ( ) a b ,使等式 f b f a f b a ( ) ( ) ( )( ) − = − 成立. 拉格朗日中值定理的其它形式: f b f a ( ) ( ) − = f a b a b a ( ( ))( ) + − − , 0 1 ; 0 0 f x f x f x x ( ) ( ) ( )( ) = + − , 在 0 x 与 x 之间; 0 0 0 0 f x f x f x x x x x ( ) ( ) ( ( ))( ) = + + − − , 0 1 ; 0 0 f x h f x f h ( ) ( ) ( ) + = + , 在 0 x 与 0 x h + 之间. 3.柯西(Cauchy)中值定理 如果函数 f x( ) 及 F x( ) 满足 (1)在闭区间 [ , ] a b 上连续; (2)在开区间 ( , ) a b 内可导; (3)对任一 x a b ( , ) , F x ( ) 0 , 那么在 ( , ) a b 内至少有一点 ( ) a b ,使等式 ( ) ( ) ( ) ( ) ( ) ( ) f b f a f F b F a F − = − 成立. 注 1 中值定理中罗尔定理可以认为是最基本的,因为其它两个中值定理均能用它导 出,而拉格朗日中值定理是最常用的; 注 2 罗尔定理、拉格朗日中值定理和柯西中值定理的条件都是充分条件但不是必要条 件. 4.泰勒(Taylor)公式 (1)泰勒(Taylor)中值定理 如果函数 f x( ) 在含有 0 x 的某个开区间 ( , ) a b 内具有直 到( n +1 )阶的导数,则对任一 x a b ( , ) ,有 0 2 0 0 0 0 ( ) ( ) ( ) ( )( ) ( ) 2! f x f x f x f x x x x x = + − + − ( ) 0 0 ( ) ( ) ! n n f x x x n + + − ( ) +R x n , 其中 ( 1) 1 0 ( ) ( ) ( ) ( 1)! n n n f R x x x n + + = − + ( 是在 0 x 与 x 之间的某个值),称 ( ) R x n 为拉格朗日型余项. 注 上面四个中值定理之间的关系图

推广 推 罗尔定理 拉格朗日中值定理 柯西中值定理 特殊情况 泰勒中值定理 (2)具有佩亚诺(Peano)型余项的泰勒中值定理如果函数fx)在含有x的某个开 区间(a,b)内有直到n阶的导数,且f(x)在(a,b)内连续,则对任一x∈(a,b),有 e)=j+f%X-+型x-x护++x-y+d-y1. 2 称R(x)=dx-无r门为佩亚诺(Peano)型余项。 注在上述两个中值定理中取飞,=0后得到的公式称为麦克劳林公式,几个常用函数的 麦克劳林公式: e=1+x++.++o(x)(0<x<+o): cosx=1- 2+-石++少22+)<: =l++f++r+ar)elcx<: 0+r=1+m+mm-少++mm-l-m-n+Dx+o)-1<x<. 21 (二)洛必达法则 定义如果当x→a(或x→o)时,两个函数fx)与F(x)都趋于零或都趋于无穷大, 事么极限四得(成一得)称为或二数未定式 定理1(洛必达法则)设 (1)limf(x)=limF(x)=0; (2)在点a的某去心邻域内,f(x)及F(x)都存在且F(x)≠0: G)四得存在(碳为无方大,影么 得得 注对于x→0时的未定式号,以及对于x→口或x→西时的未定式号,也有相应的
(2)具有佩亚诺(Peano)型余项的泰勒中值定理 如果函数 f x( ) 在含有 0 x 的某个开 区间 ( , ) a b 内有直到 n 阶的导数,且 ( ) ( ) n f x 在 ( , ) a b 内连续,则对任一 x a b ( , ) ,有 0 2 0 0 0 0 ( ) ( ) ( ) ( )( ) ( ) 2! f x f x f x f x x x x x = + − + − ( ) 0 0 ( ) ( ) ! n n f x x x n + + − 0 [( ) ]n + − o x x . 称 0 ( ) [( ) ]n R x o x x n = − 为佩亚诺(Peano)型余项. 注 在上述两个中值定理中取 0 x = 0 后得到的公式称为麦克劳林公式,几个常用函数的 麦克劳林公式: 2 1 ( ) ( ) 2! ! n x n x x e x o x x n = + + + + + − + ; 3 5 2 1 1 2 1 sin ( 1) ( ) ( ) 3! 5! (2 1)! n x x x n n x x o x x n − + − = − + − + − + − + − ; 2 4 6 2 2 1 2 2 cos 1 ( 1) ( ) ( ) 2! 4! 6! (2 2)! n x x x x n n x o x x n − + − = − + − + + − + − + − ; 2 3 1 ( 1) ln(1 ) ( ) ( 1 1) 2 3 n x x n n x x x o x x n + − + = − + − + + − ; 1 2 1 ( ) ( 1 1) 1 n n x x x o x x x = + + + + + − − ; 2 ( 1) ( 1).( 1) (1 ) 1 ( ) ( 1 1) 2! ! m n n m m m m m n x mx x x o x x n − − − + + = + + + + + − . (二)洛必达法则 定义 如果当 x a → (或 x → )时,两个函数 f x( ) 与 F x( ) 都趋于零或都趋于无穷大, 那么极限 ( ) lim ( ) x a f x → F x (或 ( ) lim ( ) x f x → F x )称为 0 0 或 型未定式. 定理 1(洛必达法则) 设 (1) lim ( ) lim ( ) 0 x a x a f x F x → → = = ; (2)在点 a 的某去心邻域内, f x ( ) 及 F x ( ) 都存在且 F x ( ) 0 ; (3) ( l ) m ) i ( x a f x → F x 存在(或为无穷大),那么 lim lim ( ) ( ) ( ) ( ) x a x a f x f x → → F x F x = . 注 对于 x → 时的未定式 0 0 ,以及对于 x a → 或 x → 时的未定式 ,也有相应的 推 广 泰勒中值定理 特 殊 情 况 罗尔定理 拉格朗日中值定理 推广 特殊情况 推广 柯西中值定理

洛必达法则.例如,对于x→a时的未定式”,有以下定理: 定理2(洛必达法则) 设 (1)limf(x)=limF(x)= (2)在点a的某去心邻域内,f(x)及F(x)都存在且Fx)≠0: G)-需华在(成为无穷大,事么 得得 (三)函数的单调性 定理设函数f(x)在[a,上连续,在(a,b)内可导,若f"(x)>0f"(x)f),那么就称)是函数f)的一个极大值(或 极小值). 2.判定条件 (1)必要条件若函数fx)在x,处可导且在x,处取极值,则f"(x)=0. 注可导函数∫x)的极值点必定是驻点.但反过来,函数的驻点却不一定是极值点, (2)第一充分条件设f(x)在x处连续,且在x,的某去心邻域U(x,)内可导. a.若x∈(-6,x时,fx)>0,而x∈(,+)时,fx)0,则fx)在。处取 得极小值: c.若x∈U(x,6)时,f()符号保持不变,则f)在x,处无极值 注由第一充分条件知,函数的驻点、不可导点是可能的极值点。 (3)第二充分条件设∫x)在x,处具有二阶导数且fx)=0,(x)≠0,那么 a.当∫"(x)0时,函数fx)在x处取得极小值. 注第二充分条件只适用于∫(x)≠0且∫(x)=0的情形,当∫化)=0或者f"(x)不 存在时用第一充分条件来判定。 (五)函数的最值 1.设函数f(x)在[a,b)上连续,在(a,b)内除有限个点外可导,且至多有有限个驻点
洛必达法则.例如,对于 x a → 时的未定式 ,有以下定理: 定理 2(洛必达法则) 设 (1) lim ( ) lim ( ) x a x a f x F x → → = = ; (2)在点 a 的某去心邻域内, f x ( ) 及 F x ( ) 都存在且 F x ( ) 0 ; (3) ( l ) m ) i ( x a f x → F x 存在(或为无穷大),那么 lim lim ( ) ( ) ( ) ( ) x a x a f x f x → → F x F x = . (三)函数的单调性 定理 设函数 f x( ) 在 [ , ] a b 上连续,在 ( , ) a b 内可导,若 f x f x ( ) 0( ( ) 0) ,x a b ( , ) , 则 f x( ) 在 [ , ] a b 上单调增加(减少). 注 将这个定理中的闭区间换成其它各种区间(包括无穷区间),那么结论也成立. (四)函数的极值 1.定义 设函数 f x( ) 在点 0 x 的某邻域 0 U x( ) 内有定义,如果对于某去心邻域 0 0 U x( ) 内 的任一 x ,有 0 f x f x ( ) ( ) (或 0 f x f x ( ) ( ) ),那么就称 0 f x( ) 是函数 f x( ) 的一个极大值(或 极小值). 2.判定条件 (1)必要条件 若函数 f x( ) 在 0 x 处可导且在 0 x 处取极值,则 0 f x ( ) 0 = . 注 可导函数 f x( ) 的极值点必定是驻点.但反过来,函数的驻点却不一定是极值点. (2)第一充分条件 设 f x( ) 在 0 x 处连续,且在 0 x 的某去心邻域 0 0 U x( , ) 内可导. a.若 0 0 x x x − ( , ) 时, f x ( ) 0 ,而 0 0 x x x + ( , ) 时, f x ( ) 0 ,则 f x( ) 在 0 x 处取 得极大值; b.若 0 0 x x x − ( , ) 时, f x ( ) 0 ,而 0 0 x x x + ( , ) 时, f x ( ) 0 ,则 f x( ) 在 0 x 处取 得极小值; c.若 0 0 x U x ( , ) 时, f x ( ) 符号保持不变,则 f x( ) 在 0 x 处无极值. 注 由第一充分条件知,函数的驻点、不可导点是可能的极值点. (3)第二充分条件 设 f x( ) 在 0 x 处具有二阶导数且 0 f x ( ) 0 = , 0 f x ( ) 0 ,那么 a.当 0 f x ( ) 0 时,函数 f x( ) 在 0 x 处取得极大值; b.当 0 f x ( ) 0 时,函数 f x( ) 在 0 x 处取得极小值. 注 第二充分条件只适用于 0 f x ( ) 0 且 0 f x ( ) 0 = 的情形,当 0 f x ( ) 0 = 或者 0 f x ( ) 不 存在时用第一充分条件来判定. (五)函数的最值 1.设函数 f x( ) 在 [ , ] a b 上连续,在 ( , ) a b 内除有限个点外可导,且至多有有限个驻点

则求f(x)在[a,b)上的最大值和最小值的方法如下: (1)求出fx)在(a,)内的驻点,玉,.,xn及不可导点,x: (2)计算fgi=l,2.m),f八xi=l,2))及fa),fb): (3)比较(2)中各个值的大小,其中最大的便是fx)在a,b]上的最大值,最小的便 是f(x)在a,b上的最小值. 2.实际问题最值的求法: (1)建立目标函数 (2)求最值. 注若目标函数(x)在其定义区间/上处处可导,且在其定义区间/内部只有唯一的驻 点。,由问题的实际意义能够判定所求最值存在且必在1内取到,则可立即断言(x,)就是 所求的最值. (六)曲线的凹凸性及拐点 1.定义设函数fx)在区间I内连续,如果对1上任意两点x,恒有 5), 2 那么称∫(x)在I上的图形是(向上)凹的(或凹弧):如果恒有 5)>2, 那么称x)在I上的图形是(向上)凸的(或凸弧).拐点是连续曲线上四凸性的分界点。 2.判定定理 定理1如果fx)在[a,上连续,在(a,b)内具有一阶和二阶导数,若在(a,b)内 (1)∫(x)>0,则fx)在a,上的图形是凹的: (2)∫(x)<0,则fx)在a,b上的图形是凸的. 定理2设y=∫x)在x=x的某个邻域内具有三阶连续导数,如果∫)=0,而 了x)≠0,则(,f化》是拐点. (七)浙近线 1.若1imf八x)=A(或1imfx)=A1imfx)=A),则y=A是y=fx)的图形的水平 渐近线: 2.若mf)=0(或imfx)=o,mf)=A),则x=。是y=f)的图形的铅直 渐近线: 3.若m国=k及回V)-树b,则y=+b是y=)的斜渐近线。 (八)曲率
则求 f x( ) 在 [ , ] a b 上的最大值和最小值的方法如下: (1)求出 f x( ) 在 ( , ) a b 内的驻点 1 x , 2 x ,, m x 及不可导点 1 x , 2 x ,, n x ; (2)计算 ( )( 1,2 ) i f x i m = , ( )( 1,2 ) i f x i n = 及 f a( ) , f b( ) ; (3)比较(2)中各个值的大小,其中最大的便是 f x( ) 在 [ , ] a b 上的最大值,最小的便 是 f x( ) 在 [ , ] a b 上的最小值. 2.实际问题最值的求法: (1)建立目标函数; (2)求最值. 注 若目标函数 f x( ) 在其定义区间 I 上处处可导,且在其定义区间 I 内部只有唯一的驻 点 0 x ,由问题的实际意义能够判定所求最值存在且必在 I 内取到,则可立即断言 0 f x( ) 就是 所求的最值. (六)曲线的凹凸性及拐点 1.定义 设函数 f x( ) 在区间 I 内连续,如果对 I 上任意两点 1 x , 2 x 恒有 1 2 1 2 ( ) ( ) ( ) 2 2 x x f x f x f + + , 那么称 f x( ) 在 I 上的图形是(向上)凹的(或凹弧);如果恒有 1 2 1 2 ( ) ( ) ( ) 2 2 x x f x f x f + + , 那么称 f x( ) 在 I 上的图形是(向上)凸的(或凸弧).拐点是连续曲线上凹凸性的分界点. 2.判定定理 定理 1 如果 f x( ) 在 [ , ] a b 上连续,在 ( , ) a b 内具有一阶和二阶导数,若在 ( , ) a b 内 (1) f x ( ) 0 ,则 f x( ) 在 [ , ] a b 上的图形是凹的; (2) f x ( ) 0 ,则 f x( ) 在 [ , ] a b 上的图形是凸的. 定理 2 设 y f x = ( ) 在 0 x x = 的某个邻域内具有三阶连续导数,如果 0 f x ( ) 0 = ,而 0 f x ( ) 0 ,则 0 0 ( , ( )) x f x 是拐点. (七)渐近线 1.若 lim ( ) x f x A → = (或 lim ( ) , lim ( ) x x f x A f x A →+ →− = = ),则 y A = 是 y f x = ( ) 的图形的水平 渐近线; 2.若 0 lim ( ) x x f x → = (或 0 0 lim ( ) , lim ( ) x x x x f x f x A → → + − = = ),则 0 x x = 是 y f x = ( ) 的图形的铅直 渐近线; 3.若 ( ) ( ) lim x x x f x k → x →+ →− = 及 ( ) lim ( ) x x x f x kx b → →+ →− − = ,则 y kx b = + 是 y f x = ( ) 的斜渐近线. (八) 曲率

1.在(a,b)上具有连续导数的函数y=f)的弧微分:d本=√+y产k 2.定义比值,即单位弧段上切线转过的角度大小,称为M到N弧段的平均曲率: 极限K=四称为曲线y=)在点M(x)的曲率, 曲率的倒数上称为曲线y=x)在点M(x,)的曲率半径:K=0时称这曲率半 径为无穷大. 在曲线M处的法线上四的一侧取一点D,使DM=文=p,以D中心,p为半径的圆, 称为曲率圆. 3.曲率的计算公式 当y=fx)具有二阶导数时,K= 0+2厅 =p0给出时,则K=l-u1 当曲线是由参数方程=0 V@?+w厅
1.在 ( , ) a b 上具有连续导数的函数 y f x = ( ) 的弧微分: 2 ds y dx = +1 2.定义 比值 s ,即单位弧段上切线转过的角度大小,称为 M 到 N 弧段的平均曲率; 极限 0 lim s K s → = 称为曲线 y f x = ( ) 在点 M( x f x , ( ) )的曲率. 曲率的倒数 1 K 称为曲线 y f x = ( ) 在点 M( x f x , ( ) )的曲率半径; K = 0 时称这曲率半 径为无穷大. 在曲线 M 处的法线上凹的一侧取一点 D,使 1 DM K = = ,以 D 中心, 为半径的圆, 称为曲率圆. 3.曲率的计算公式 当 y f x = ( ) 具有二阶导数时, 2 3 | | (1 ) y K y = + . 当曲线是由参数方程 ( ) ( ) x t y t = = 给出时,则 2 2 3 ( ) K − = + .