
第十一章微分方程 数学实验 一、常微分方程符号解的求解 用Matlab函数dsolve求常微分方程 F(xyy,yy.y)=0 的通解的主要调用格式如下: S=dsolve('ean','var') 其中输入的量eqn是改用符号方程表示的常微分方程F(x,y,Dy,d2y,Dny)=0,导数用 D表示,2阶导数用D2表示,以此类推.v阳r表示自变量,默认的自变量为t.输出量S是常 微分方程的解析通解. 如果给定常微分方程(7.1)的初始条件)=4,y()=a,.,y(x)=a,则求方程 (7.1)的特解的主要调用格式如下: S=dsolve('egn','condition1 ',.'conditonn ','var') 常微背籍价得的合文如上 conditionl,.conditonn是初始条件.输出量S是 例1求下列常微分方程的通解 解求通解相应的Matlab程序为 >xl=dsolve('Dx=-a*x'), >y2=dsolve('D2y+a*dy=b*(sin(x)+cos(x))','x'), >》y3=dsolveDy=y^2*(1-y)'), y4-dsolve(D2y=sin()) 运行后可得常微分方程(1)入(2、(3)、(4)的通解x1、y2、y3、y4依次如下 x1 =Cl*exp(-a*t) y2 =b*(-sin(x)-cos (x))-1/2*a*dy*x"2+C1*x+C2 y3=1/(1 ambertw(-1/C1*exp(-t-1)+1) y4=nt/-2*cos(a)C)/2-a=.)-t-C2=0 nt(-1/( c1(1/9 -t-C2=0 其中C1和C2是任意常数.因为常微分方程(3)和(4)的显式解没有被找到,所以返回隐 式解. 例2求下列常微分方程在给定初始条件下的特解。 f-y,o,=lgy倒 =0. dx 解求特解相应的Matlab代码为 >f=dsolve ('D2f=-a"2*Df','f(0)=1,Df(pi/a)=0') 运行后得常微分方程在给定初始条件下的特解「如下 例3已知需求与供给函数为
1 第十一章 微分方程 数学实验 一、常微分方程符号解的求解 用 Matlab 函数 dsolve 求常微分方程 ( ) ( , , , , , , ) 0 n F x y y y y y = 的通解的主要调用格式如下: S=dsolve('eqn', 'var') 其中输入的量 eqn 是改用符号方程表示的常微分方程 F(x,y,Dy,d2y,.Dny)=0,导数用 D 表示,2 阶导数用 D2 表示,以此类推.var 表示自变量,默认的自变量为 t.输出量 S 是常 微分方程的解析通解. 如果给定常微分方程(7.1)的初始条件 ( ) 0 0 0 1 0 ( ) , ( ) , , ( ) n n y x a y x a y x a = = = ,则求方程 (7.1)的特解的主要调用格式如下: S=dsolve('eqn', 'condition1 ',.'conditonn ','var') 其中输入量 eqn,var 的含义如上, condition1,.conditonn 是初始条件.输出量 S 是 常微分方程的特解. 例 1 求下列常微分方程的通解 d (1) d x at t = − ; 2 2 d d (2) (sin cos ) d d y y a b x x x x + = + ; d 2 (3) (1 ) d y y y x = − ; (4) 2 2 d sin d y y x = . 解 求通解相应的 Matlab 程序为 >> x1=dsolve('Dx=-a*x'), >> y2=dsolve('D2y+a*dy=b*(sin(x)+cos(x))','x'), >> y3=dsolve('Dy=y^2*(1-y)'), >> y4=dsolve('D2y=sin(y)'), 运行后可得常微分方程(1)、(2)、(3)、(4)的通解 x1、y2、y3、y4 依次如下 x1 =C1*exp(-a*t) y2 =b*(-sin(x)-cos(x))-1/2*a*dy*x^2+C1*x+C2 y3 =1/(lambertw(-1/C1*exp(-t-1))+1) y4 =Int(1/(-2*cos(_a)+C1)^(1/2),_a = . y)-t-C2 = 0 Int(-1/(-2*cos(_a)+C1)^(1/2),_a = . y)-t-C2 = 0 其中 C1 和 C2 是任意常数.因为常微分方程(3)和(4)的显式解没有被找到,所以返回隐 式解. 例 2 求下列常微分方程在给定初始条件下的特解. 2 2 2 d ( ) d ( ) d ( ) , (0) 1, 0 d d d x a f x f x f x a f x x x = = − = = . 解 求特解相应的 Matlab 代码为 >> f=dsolve('D2f=-a^2*Df','f(0)=1,Df(pi/a)=0') 运行后得常微分方程在给定初始条件下的特解 f 如下 f =1 例 3 已知需求与供给函数为

Qa=12-2P+P'+3P",Q.=-4+6P-P'+2P”. 初始条件为P(O)=10,P'(O)=4.假设在每一刻市场均是出清的,求P(). 解由Q=Q.得 p"+2P'-8P=-16 求给定初始条件P(O)=10,P'(O)=4的微分方程特解的Matlab程序为 >p=dsolve('D2p+2*p-8*p=-16','p(O)=10','Dp(0)=4') 运行结果为 p=6*exp(2*t)+2*exp(4*t)+2 因此特解为P()=6e2”+2e4+2, 二、常微分方程的数值解求解 、少数特殊方程可用初等积分法求解外,大部 y't)=fl.).l。y=dsolve ('Dy=-y+t+1','y(0)=1','t') 运行结果为y=t+exp(~t),即方程的解析解为y=1+e'.下面再求其数值解,先编写M文件 funl.m. function f=funl(t,y)
2 Q 12 2P P 3P , d = − + + Qs = −4 + 6P − P + 2P . 初始条件为 P(0) = 10, P(0) = 4 . 假设在每一刻市场均是出清的,求 P(t) . 解 由 Qd = Qs 得 P + 2P −8P = −16 求给定初始条件 P(0) = 10, P(0) = 4 的微分方程特解的 Matlab 程序为 >> p=dsolve('D2p+2*Dp-8*p=-16','p(0)=10','Dp(0)=4') 运行结果为 p =6*exp(2*t)+2*exp(-4*t)+2 因此特解为 ( ) 6e 2e 2 2 4 = + + t − t P t . 二、常微分方程的数值解求解 除常系数线性微分方程可用特征根法求解、少数特殊方程可用初等积分法求解外,大部 分微分方程无解析解,应用中主要依靠数值解法.考虑一阶常微分方程初值问题 0 0 0 ( ) ( , ( )), ( ) f y t f t y t t t t y t y = = 其中 1 2 ( , , , )T m y y y y = , 1 2 ( , , , )T m f f f f = , 0 10 20 0 ( , , , )T m y y y y = .所谓数值解法,就 是寻求 yt() 在一系列离散节点 0 1 n f t t t t 上的近似值 , 0,1, , k y k n = ,称 k k k 1 h t t = − + 为 步长,通常取为常量 h .最简单的数值解法是 Euler 法. Euler 法的思路很简单:在节点处用差商近似代替导数 1 ( ) ( ) ( ) k k k y t y t y t h + − 这样导出计算公式 1 ( , ), 0,1,2, k k k k y y hf t y k + = + = 它能求解各种形式的微分方程.Euler 法也称折线法. Euler 法只有一阶精度,改进方法有二阶 Runge-Kutta 法、四阶 Runge-kutta 法、五阶 Runge-kutta-Felhberg 法和线性多步法等,这些方法可用于解高阶常微分方程(组)初值问 题.边值问题采用不同方法,如差分法、有限元法等.数值解法的主要缺点是它缺乏物理意义. Matlab 中主要用函数 ode45,ode23,ode15s 求常微分方程的数值解.其中 ode45 是最常 用的求解微分方程数值解的命令,对于刚性方程组不宜采用.ode23 与 ode45 类似,只是精度 低一些.ode15s 用来求解刚性方程组.这三个函数的调用格式基本相同,下面介绍 ode45 的调 用格式. [tout,yout]=ode45(‘yprime’,[t0,tf],y0) 此命令是采用变步长四阶 Runge-kutta 法和五阶 Runge-kutta-Felhberg 法求数值解, yprime 是表示 f(t,y)的 M 文件名,t0 表示自变量的初始值,tf 表示自变量的终值,y0 表示 初始向量值.输出向量 tout 表示节点 0, 1 ( , , )T n t t t ,输出矩阵 yout 表示数值解,每一列对应 y 的一个分量.若无输出参数,则自动作出图形. 例 4 求解微分方程 d 1, (0) 1 d y y t y t = − + + = 的解析解和数值解,并进行比较. 解 相应的 Matlab 代码为 >> y=dsolve('Dy=-y+t+1','y(0)=1','t') 运行结果为 y =t+exp(-t),即方程的解析解为 e t y t − = + .下面再求其数值解,先编写 M 文件 fun1.m. function f=fun1(t,y)
f=-y+t+l: 再运行相应的atlab代码 >clear;close;t=0:0.1:1; >y=t+exp(-t);plot(t,y); %画解析解的图形 >hold on: %保留已经画好的图形,如果下面再画图,两个图形合并在一起 >》=ode45Cfun',【0,1. >plot (t.y,'ro') %画数值解图形,用红色小圈西 >xlabel('t'),ylabel('y') 运行结果见图11-7. 13 02030.40506070.80 图11-1 3
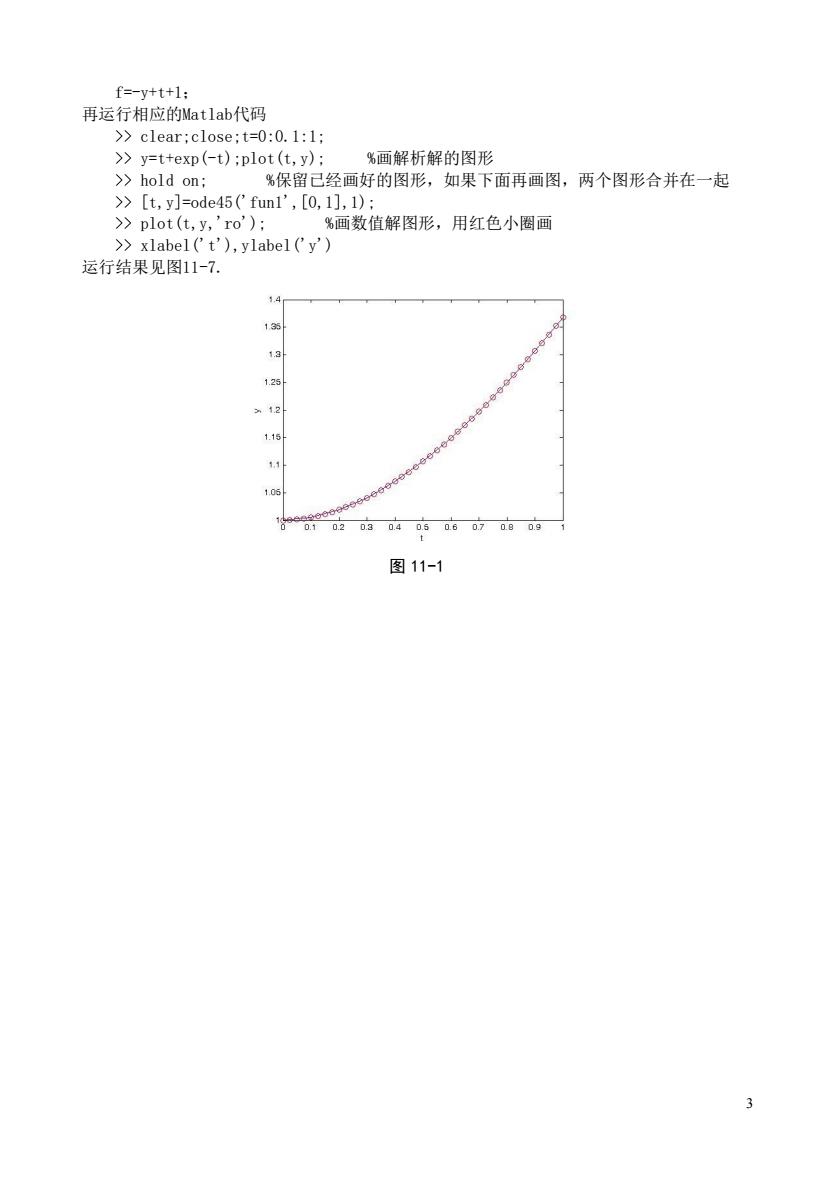
3 f=-y+t+1; 再运行相应的Matlab代码 >> clear;close;t=0:0.1:1; >> y=t+exp(-t);plot(t,y); %画解析解的图形 >> hold on; %保留已经画好的图形,如果下面再画图,两个图形合并在一起 >> [t,y]=ode45('fun1',[0,1],1); >> plot(t,y,'ro'); %画数值解图形,用红色小圈画 >> xlabel('t'),ylabel('y') 运行结果见图11-7. 图 11-1